磁敏弹性体的制备及磁致响应模型的研究概述
2018-07-23张胜强芮晓丽徐坚栋
张胜强,芮晓丽,徐坚栋,张 营
[1.中国汽车技术研究中心有限公司,天津 300300;2.天津市城市规划设计研究院,天津 300202;3.山东黄金矿业(玲珑)有限公司,山东 烟台 265400]
目前,隔振降噪的吸能材料与结构广泛应用,但绝大多数是传统的吸能材料与结构,它们在规定载荷下能够保持一定的强度与刚度。该类材料通过变形来实现的能量转换是单方向、不可逆的,即输入的冲击能量,通过材料与结构的塑性变形或其他形式的吸收耗散,使动能转换成非弹性能。传统的吸能材料与结构的吸能方式为被动式吸能,其吸能的主要参数——刚度和阻尼保持固定。刚度和阻尼可变的智能材料受到了越来越多的关注和研究,并应用于许多机械的吸能结构中。
磁敏弹性体作为智能材料的一种,其刚度和阻尼能够随外加磁场的磁感应强度的改变而变化。磁敏弹性体是将微米尺度的增强颗粒(主要为羟基铁颗粒)均匀分散到液态高分子橡胶中,并在强磁场中固化形成复合材料,增强颗粒在橡胶基体中呈链状排列。在磁敏弹性体的应用过程中,未达到磁饱和前,当磁感应强度大小变化时,经过磁化的颗粒间相互作用,其刚度和阻尼特性可以在几毫秒的时间内随之改变[1-2]。因此,磁敏弹性体的增强颗粒排列有序程度直接影响其磁场响应特性。在多种交通工具和机械设备中,磁敏弹性体可用于冲击或振动的自适应衰减装置[3-5]中,应用前景十分广阔。
1 制备材料及工艺
将磁敏弹性体的基体材料和增强颗粒以适当的用量比例混合,同时添加石墨、硅油和其他添加剂成分,可以获得良好的磁敏特性和力学性能。
1.1 基体材料
基体材料的选择有天然橡胶和硅橡胶、热塑性橡胶等合成橡胶[6-8]。不同橡胶的磁敏弹性体性能差异较大,例如2004年,Y.Shen等[9]提出聚氨酯基的磁敏弹性体相对于天然橡胶基的磁敏弹性体具有更显著的磁敏效应;2007年,L.Chen等[10]研究得出在零磁场下,天然橡胶基的磁敏弹性体相对于硅橡胶基的磁敏弹性体具有更高的刚度,且通过添加硅油等添加剂可以降低刚度。
1.2 增强颗粒
磁敏弹性体的磁敏效应主要来自于外加磁场对增强颗粒的作用。J.D.Carlson等[11]的研究显示,磁敏效应对铁颗粒产生的磁透性具有较高的饱和度和较低的剩磁效果,所以磁敏弹性体增强颗粒的研究以铁颗粒为主。
通过研究[12-16]得出,高体积分数的铁颗粒产生高的磁敏效应。针对低体积分数的铁颗粒,可以通过添加辅助剂来改善其性能。2008年,L.Chen等[17]通过添加辅助试剂来增大磁敏弹性体的刚度,例如炭黑等材料。2012年,A.Alberdi-Muniain等[18]研究发现,磁敏弹性体剪切模量增大幅度随着炭黑、铁颗粒、增塑剂用量的增大而更加明显。2012年,M.Yu等[19]发现,添加炭黑还可以增大磁敏弹性体的磁敏效应和磁致剪切模量,同时有助于提高磁敏弹性体导电性。
2009—2011年,I.Bica等[20-23]发现磁敏弹性体可以应用于磁阻传感器等方面。2012年,X.Gong等[24]通过添加聚己内酯来改善磁敏弹性体的阻尼性能。2013年,Y.Han等[25]通过改变增强颗粒的尺寸和形状来调整磁敏效应,改变磁敏弹性体的磁化强度和应变灵敏度,同时还研究了铁颗粒和镍颗粒[26]对于磁敏效应的影响。
1.3 制备工艺
目前磁敏弹性体的制备工艺包括A.Fuchs等[27]提出的注射成型、铸造成型、B.K.S.Woods等[28]提出的真空辅助树脂传递成型以及其他方法[29-32]。此外,A.Fuchs等[33]在固化中采用外加磁场的方法,使结构链状粒子沿磁场方向排列,并促进各成分间的化学交联。
2 增强颗粒相互作用的模型
2.1 准各向同性模型
如果磁敏弹性体在零磁场的环境下固化,增强颗粒会分布均匀,一般将此类磁敏弹性体视为准各向同性材料。2007年,G.V.Stepanov等[34]通过将相连的增强颗粒简化为一系列的弹性杆件,用来定义各向同性的磁敏弹性体模型。
2.2 各向异性模型
2.2.1 旋转效应理论
磁敏性弹性体的研究集中于各向异性的磁敏弹性体,2006年E.Coquelle等[35]采用解析和数值模拟的方法得出,磁敏弹性体较高的局部应力引起增强颗粒与基体之间的剥离。尤其是非球形的增强颗粒,在受到磁场作用时产生的磁力矩引发旋转效应,这种效应取决于基体对其的弹性扭转力矩[36-38]。
一些学者研究得出,在增强颗粒分布良好的情况下,基体的弹性会产生高达10%的应变。当施加单方向的磁场,可以得出以下平衡方程:
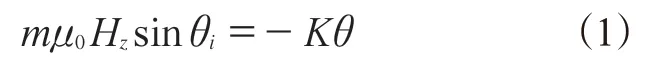
式中,m为增强颗粒磁矩,μ0为真空磁导率,Hz为Z轴方向磁场强度,θi为m方向与Hz方向的初始夹角,K为弹性力矩常数,θ为增强颗粒有效旋转角度。
2.2.2 平均磁矩理论
2004年,L.Lanotte等[39]在评估磁敏弹性体宏观性能的过程中,采用了平均磁矩的研究方法,并采用直接磁致伸缩效应试验对该方法进行了验证。由于弹性材料变形,在逆磁致伸缩效应研究中需要考虑磁化轴的变化。基于磁场同方向的外应变分量的研究,认为增强颗粒的旋转角度θε仅由应变εz决定:
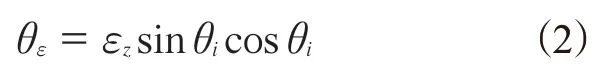
结合式(1)可得:
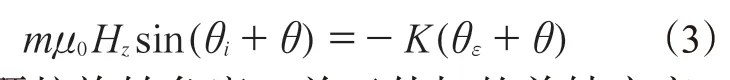
基于增强颗粒旋转角度θ,关于外加的单轴应变εz和磁场强度Hz的本构方程可以表示为:式中,m*为施加磁场后的增强颗粒磁矩。
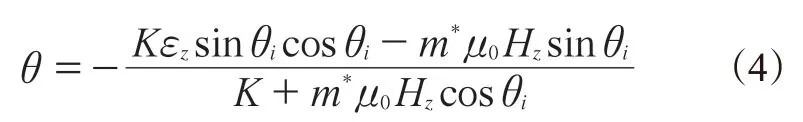
2.2.3 偶极矩理论
1996年,M.R.Jolly等[40-41]采用半经验的本构模型(基于一个两参数的增强颗粒偶极矩,两个参数通过试验数据计算得出),对磁敏弹性体的磁敏特性进行了研究。数据显示在外加磁场的条件下,磁敏弹性体的剪切模量变化率可达到30%以上,该数据在磁敏弹性体双搭接剪切模型的试验中得到了验证。由此,基于磁敏效应,提出了磁敏弹性体的应力-应变关系的准静态模型,并采用聚氨酯和天然橡胶两种不同基体的磁敏弹性体验证了该准静态模型。
2006年,Z.Varga等[42]根据施加的磁场方向、增强颗粒链的方向、磁敏弹性体受力的方向,研究了几种不同工况下磁敏弹性体的剪切模量。沿着力FX方向的主应变λX可以表示为

式中,hX为X轴方向的变形长度,h0为X轴方向的原始长度。整体能量密度W由两部分组成:
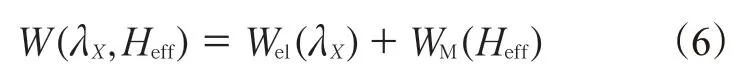
式中,Wel是弹性能,它是主应变λX的函数;WM是磁场能,它是有效磁场强度Heff的函数。
基于式(6),在均匀磁场条件下,试验测得的剪切模量G为

式中,G0为材料的初始剪切模量,表示施加磁场后增加的磁致剪切模量。磁致剪切模量的解析计算值与磁场能相关。
2.3 试验验证
通过力学性能试验,研究了静磁场下,磁感应强度B与磁致剪切模量GME的函数关系。结果[42]显示,在低磁场强度下,磁致剪切模量的变化量与磁感应强度的平方正比,在高磁场强度下,磁致剪切模量的变化量逐渐减小,剪切模量趋近于最大值,这一现象可表示为

3 磁-粘-弹响应模型
磁敏弹性体磁致响应模型主要研究磁场下静态载荷作用和动态冲击载荷作用。基于固体力学的磁敏弹性体的磁致响应研究可以追溯到1960年。这类模型的理论可以分为连续介质力学守恒理论和能量最小化理论。
3.1 多物理场耦合理论
即使试件几何形状和边界条件简单,在非线性和耦合的条件下,弹性大变形的复合材料的多物理场建模也是复杂的。2013年,F.Vogel等[43]使用混合变分方程的有限元法,并结合勒让德变换和拉格朗日乘子法,在外加机械载荷和磁场作用下,研究了弹性大变形。同年,A.Javili等[44]基于应变有限元的方法,开发出了复合材料非线性均匀化的大变形理论框架。
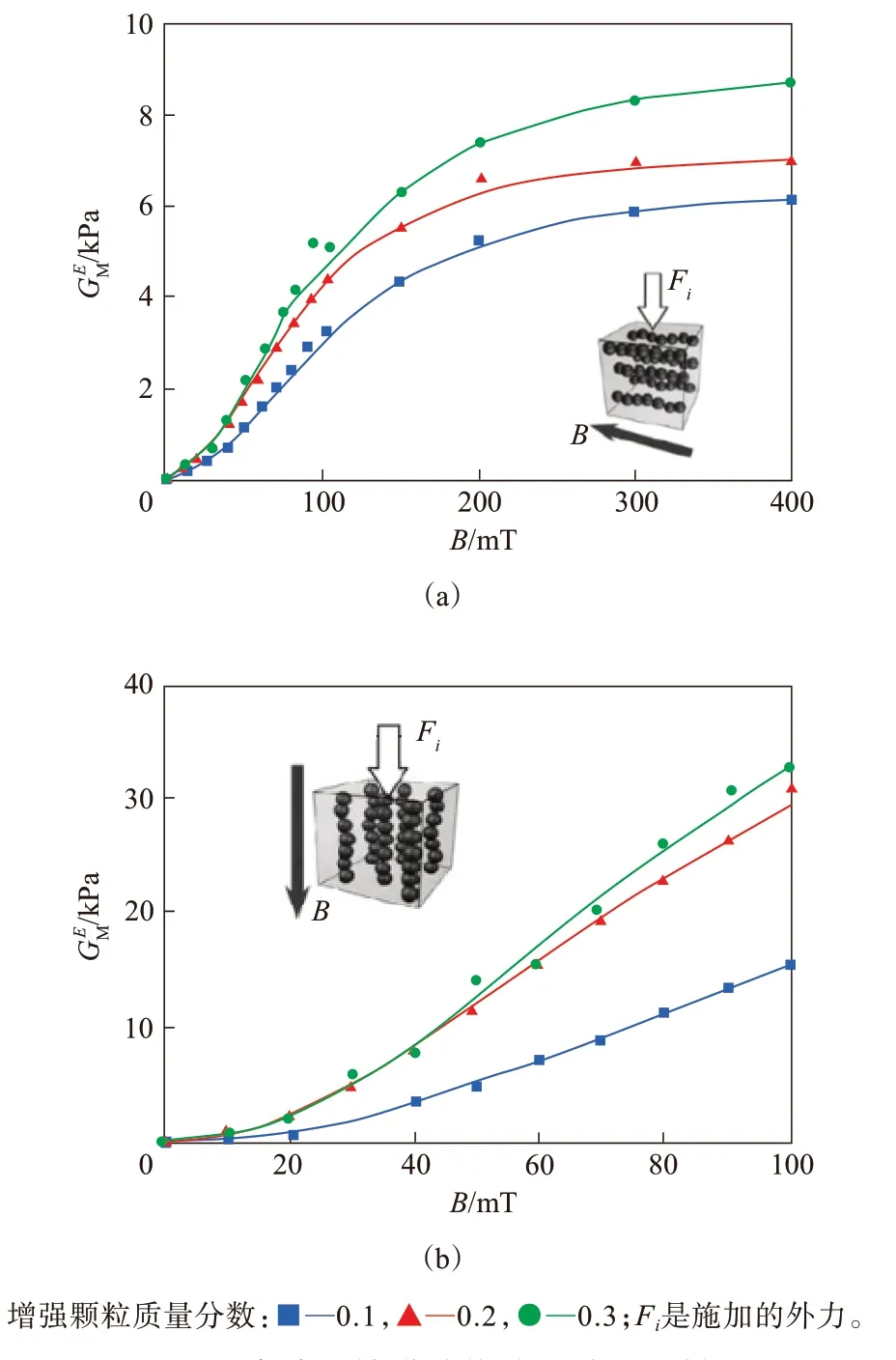
图1 硅橡胶磁敏弹性体的磁致剪切模量-磁感应强度的关系
2003年,I.A.Brigadnov等[45-46]根据磁通量和线性磁场本构方程,提出了一种基于自由能的理论闭环求解方法。然而,该方法用于解决有限尺寸的试件存在局限性。2009年,R.Bustamante[47]为了求解不同边界条件下的控制方程,采用了变分方程和数值求解相结合的方法。A.Dorfmann等[46]将有限元几何方法引入到解决非线性磁弹性的边界问题中,并计算出了数值解。2015年,R.Bustamante等[48]提出了磁敏弹性体大变形和模型线性化的隐式本构关系。
3.2 磁敏效应理论
2007年,G.V.Stepanov等[49]研究发现,用杨氏模量来衡量软体磁敏弹性体时,磁敏弹性体在低应变时具有更好的磁敏效应。同时,增强颗粒的尺寸和用量决定了磁敏效应的强弱。基于有限应变理论[50],提出了磁敏弹性体的横观各向同性能量密度函数[51]。
当嵌入的增强颗粒的刚度远大于基体材料的刚度时,磁敏弹性体的粘弹性行为主要取决于弹性基体材料的非晶态分子微观结构。粘弹性材料的特性主要体现在以下4个方面:
(1)粘弹性材料在恒定应力下,出现随时间变化的蠕变变形;
(2)粘弹性材料在恒定应变下,产生随时间变化的应力松弛现象;
(3)粘弹性材料在恒定振荡载荷下,出现应力-应变迟滞回线;
(4)粘弹性材料在不同应变加载速率下,应力-应变曲线产生应变率效应。
R.F.Gibson等[52-54]均采用一个四参数的粘弹性模型(如图2所示)推导了不同磁通密度模型的参数。发现基于材料参数k1,k2,kb,c2,可以得到不同磁场强度下的剪切储能模量(G′)和剪切损耗模量(G″):
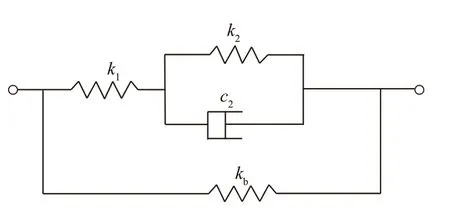
图2 磁敏弹性体的四参数弹簧-阻尼粘弹性模型
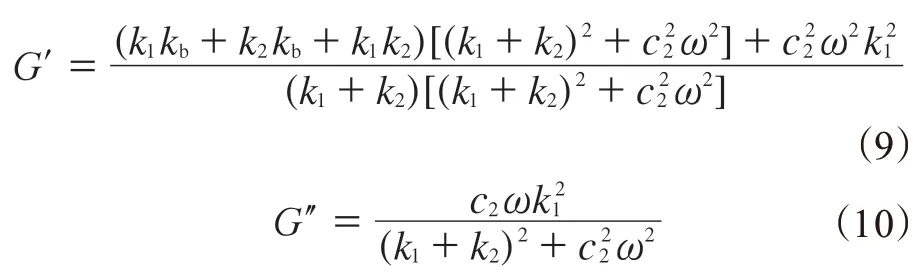
式中,ω是频率。
硅橡胶/羟基铁粉磁敏弹性体在平行板式流变计上显示的迟滞回线如图3所示,该磁敏弹性体可用上述四参数模型来预测该迟滞回线。
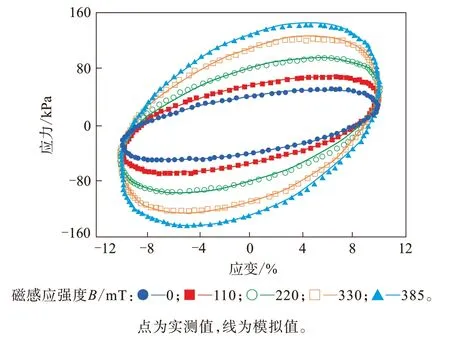
图3 不同磁感应强度下测试和线性粘弹性模型模拟的应力-应变迟滞曲线
这种迟滞回线可以用来确定复杂的模量,在剪切工况下,其复杂的剪切模量(G*)可以表示为
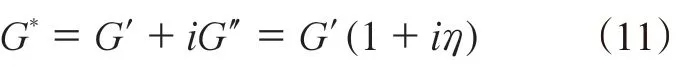
式中,η是剪切损耗因子。当磁敏弹性体的应变小于7%时,被认为处于线粘弹性范围内。2006年,E.Coquelle等[55-56]提出了磁敏弹性体的有效剪切储能模量(G*′)的计算公式:
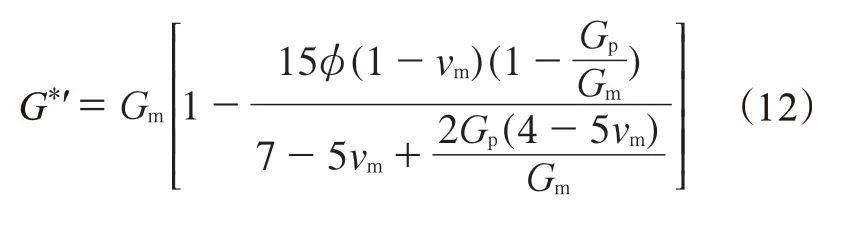
式中,Gm为基体的剪切模量,φ是增强颗粒的体积分数,vm为矩阵的泊松比,Gp是增强颗粒的剪切模量。
4 结语
以橡胶和增强颗粒制备的磁敏弹性体在减震结构中的应用不断扩展。为推动磁敏弹性体的进一步发展,必须对其磁致响应理论和模型进行更加深入的研究。
