“探索图形”教学纪实、反思与评析

韩巍 王岩

教学目标：

1.加深对正方体特征的认识和理解。

2.通过观察、列表、想象等方式探索、发现图形分类计数问题中的规律，体会化繁为简解决问题的策略。

3.培养空间想象力，体会分类、数形结合、归纳、推理、模型等数学思想。

教学重点：学会从简单的情况找规律，解决复杂问题的化繁为简的思想方法。

教学难点：探索规律的归纳方法。

教具准备：2、3、4阶魔方，学习单，课件。

教学过程：

一、 巧设障碍，引发思考

师：请大家看，黑板上出现的是什么图形？

生：正方体。

师：正方体有哪些特点呢？

生：正方体有8个顶点，12条棱和6个面。

师：同学们，如果我对这个大正方体进行切割，请看这就是切割后的图形，你们知道现在它是由多少个小正方体组成的吗？

生：这个大正方体是由729个小正方体组成的。

师：这个数据你是怎么得到的呢？

生：我发现这个大正方体长宽高都被平均分成了9份，利用求正方体的体积公式我就求出了它有729个小正方体。

师：你可真了不起，通过细致的观察，利用以前学过的知识就得到了准确的答案。

师：现在我们把这个大的组合图形的表面涂漆，你知道什么是表面涂漆吗？

生：就是把这个大正方体的外面图上漆。

师：里面涂吗？

生：里面不涂。

师：请大家猜测一下，每个小正方体的涂漆会如何呢？

生：有三面涂漆、两面涂漆、一面涂漆还有没涂上漆的。

师：为什么还有没涂上漆的呢？

生：被包在里面的就涂不上。

师：还有其他情况吗？

生：没有。

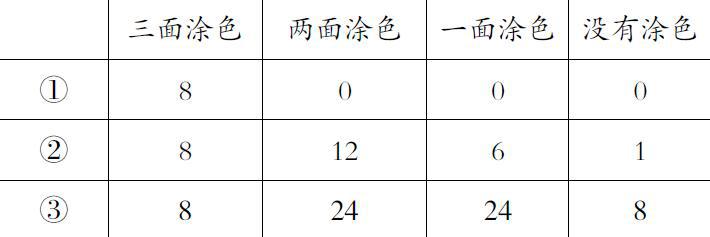
师：每一类小正方体分别有多少个呢？我们来分类填一填。（出示表格）如果请你来数一数，你有什么感觉？

生：太多了，数不过来啊！

师：看来这个图形太复杂了，数起来很麻烦，你有什么好办法解决这个问题吗？

生：我算一算。

师：你一定是有了什么方法，你是怎么得到这样的方法的呢？

生：我们化繁为简，可以研究比较简单的正方体，看看有什么规律，然后再解决这个问题。

师：下面，我们就来用这个办法尝试一下。

二、 合作探究，完成建模

（一） 尝试解决，发现规律

师：你认为什么样的图形比较简单，容易找到答案呢？

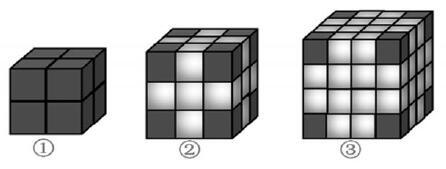
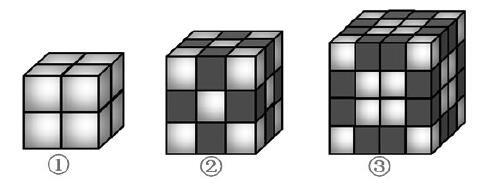
生：长宽高各有2个正方体，3个正方体，4个正方体的图形。

出示合作要求

两人一组合作研究。活动要求：

1.借助手中的魔方，数一数、算一算，把结果填在记录表中。

2.观察表中记录的数据，看看你发现了什么。

（生四人为一组合作研究。）

师：说说你的发现。

生：三面涂色的小正方体都位于大正方体的顶点的位置，都有8个。

生：三阶魔方中，两面涂色的是位于每条棱的中间，每条棱上有一个小正方体，12条棱就有12个小正方体。

师：你是怎么算出来的呢？

生：如果一条棱上有3个正方体，减去两边的正方体，就是1，再用1乘12得到12个小正方体。

师：那么四阶魔方呢？

生：一条棱上有4个正方体，减去两边的正方体，就是2，再用2乘12得到24个小正方体。

师：还有其他发现吗？

生：一面涂色的是每个面上除去外圈的小正方体。

师：你是怎么算出每个面上除去外圈的小正方体的个数呢？

生：以3阶魔方为例，一个面有9个小正方形，外圈有8个，9-8=1，面上就有1个。

师：这位同学是用一个面的总个数减去外圈的数量得到的数据。还有什么方法吗？

生：以3阶魔方为例，一个面横着看有3行小正方体，减去上下两行就是中间1行，就有1个小正方体一面涂色。

师：那么，你列的算式就是3-2=1，是吗？如果用这样的思路来解决4阶魔方可以吗？

生：不行，4-2=2，可是我们数出的是一个面有4个小正方体一面涂色啊！

生：以4阶魔方为例，一个面横着看有4行小正方体，减去上下两行就是中间2行，竖着看有4列小正方体，减去左右两列就是中间2列，2乘2就是4个小正方体一面涂色。

师：你真是一个善于观察、善于总结方法的学生，就一面涂色的情况谁还有自己的发现？

生：我发现一个面的正方形个数就可以用求面积的方法，长是2，宽是2，2乘2就得4了，再用4乘6个面就得到了24。

师：你把求平面图形面积的方法用在了求一面涂色的块数上，真有办法。

生：我还发现用小正方体的总数量减去前三项的数量就是中间没有涂色的数量。

师：你很善于思考，还有其他方法得到没有涂色的数量吗？

生：我发现4阶魔方的里面没有涂色的就是2阶魔方，3阶魔方的里面就是1个小正方体。

生：以3阶魔方为例，我发现如果用3减2就得到1了。

生：我认为这种方法不对，如果是4阶魔方也不能用4减2啊。

师：是啊，那么怎么来数、来算呢？

生：4阶魔方有4層小正方体，去掉上下2层就剩下中间2层了，前后数共4行去掉前后2行剩下中间2行，左右数共4列去掉左右2列剩下中间2列，所以是2乘2乘2得到的8个。

师：老师这里有个非常直观的课件，谁愿意像他描述的这样来操作一下？

（生一边操作一边讲解。）

师：看来这个中心部分的块数、我们可以借助求正方体的体积的方法得到。

师：大家看这两种算中间没有涂漆的小正方体的结果一样吗？

生：一样。

师：虽然我们看不到里面的中心部分，但是我们用这两种方法都可以解决这个问题，而且它们相互验证了结果的准确性。

（二） 应用规律，解决问题

师：大家有了这么多发现和方法，现在你们能解决稍微复杂的问题了吗？我们来试一试吧！以小组为单位算一算5×5×5、6×6×6的正方体，并继续完成表格。

汇报交流：

生：用n表示正方体的棱长（所含小正方体的块数），规律可以这样表示：三面涂色小正方体的块数=8（顶点的个数），两面涂色小正方体的块数=（n-2）×12，一面涂色小正方体的块数=（n-2）2×6，没有涂色小正方体的块数=（n-2）3。

师：你真善于总结，你在这几个公式中有什么发现吗？

生：我发现除了三面涂色是与8个顶点位置的正方体有关，其他的分别是（n-2）的一次方，（n-2）的二次方，（n-2）的三次方。

师：为什么有这样的规律呢？

生：因为求两面涂色的正方体在棱上，棱上中间有几个正方体再乘12条棱，一面涂色的正方体是在面上，要用中间长和宽相乘，而长和宽又相同，所以就是平方数乘6个面，最里面没有涂色的部分实际是个正方体，所以是立方数。

师：你善于观察和总结，把这几种涂色情况分析得真透徹。

师：现在我们再来解决课开始前的问题吧！

三、 结合实际，引发兴趣

师：在生活中，这种利用规律解决问题的情况还有很多，如金字塔图形的数量问题，正方体组成长方体涂漆问题，都可以利用我们今天学到化繁为简的方法来分析解决，还有把数学知识运用到其他领域的情况，如工程设计、美术装饰，希望同学们都能有善于发现善于总结的学习习惯，去解开更多的秘密。

反思：

“数学好玩”是我校正在探索实践的课程，它以数学学科为载体，广泛挖掘课内外学习资源，充分调动学生学习积极主动性，以培养学生数学核心素养为目标。在我执教的“探索图形”一课时，从设计到实施，也努力以此为依据。

首先，我设计了两次以小组为单位的交流实践活动，通过第一次观察、想象和推理数一数、算一算每种涂色情况，并尝试用列表的方法表示出来，逐步发现每种涂色情况的位置和规律。在此基础上，学生进行第二次活动，应用规律解决问题，在数学实践活动中学会合作、学会交流，享受成功的喜悦，体验数学学习的乐趣。

第二，我将数学思想融入到此次学习中，从数学问题的提出到引导学生利用化繁为简的数学思想解决问题，从数一数、算一算、填一填的学习活动到发现分类计数问题中的规律，从归纳、推理的研究交流到建立数形结合、完成建模的学习体验，一步一步引导学生把握问题共性的同时发展学生的空间观念及空间想象能力。

第三，在本节课中我力求深度挖掘教材，以小学阶段接触到的空间几何领域的点、线、面、体的知识体系串联本课学习内容，并与一次方、二次方、三次方的代数知识对接，让学生感受到数学学习的连贯性和递进性，体会数学领域的神奇以及学习数学的乐趣。

评析：

1.“数学好玩”让学生“玩”起来

“数学好玩”课程的显著特点之一就是让学生真正成为学习的主体，利用合作、交流以及探究等多种形式“玩”起来。本节课教师就舍得将课堂时间留给学生，第一次探究的时间为8分钟，第二次合作交流的时间为5分钟，在一节40分钟的课中，这13分钟的时间是不短的，同时课堂上采用小组活动和全员参与活动相结合的形式，让学生有了充分的活动时间和空间，提供了发现总结规律的机会，在活动中品尝到了成功的乐趣。

2.“数学好玩”体现核心素养

“数学好玩”这一课程以提升数学核心素养为中心，培养学生数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析的能力。本课教学中，教师就现有的教材进行了深入的钻研，带领学生感悟到化繁为简的数学思想，经历建立数学模型的过程，从分类计数、推理和数形结合体验中，丰富了思维活动经验，尤其是在课程接近尾声的时候，自然地揭示了三面涂色、两面涂色、一面涂色、没有涂色和点、线、面、体的关系，感知了从一维空间、二维空间到三维空间的数学模型建立体系。让学生经历将实际问题抽象成数学模型并运用的过程。

3.“数学好玩”从知识本位走向课程本位

“数学好玩”作为花园小学研发的一项课程，不是以知识为唯一或几乎以知识为唯一的教学目标，而是致力于凸显学生在课程学习中发生的变化，思维由浅入深逐步提升，学习兴趣逐渐浓厚，自信心显著提升，追求从知识本位走向课程本位。这节课中，教师关注的是如何让学生爱上数学，利用喜欢的魔方作为学具，拉近生活、游戏与学习的距离，畅谈“你的发现”培养学生习惯用数学的思维分析并解决问题，共同合作交流促进情感态度价值观的建立。

编辑/魏继军