基于Copula函数的设计暴雨雨型研究

叶姗姗， 叶兴成， 王以超， 朱程亮， 刘 俊

(1.河海大学 水文水资源学院， 江苏 南京 210098； 2.宿迁市水务局， 江苏 宿迁 223800)

1 研究背景

随着全球气候的不断变化，城市化建设进程加快和原有排水防涝系统设计标准偏低等因素，宿迁市常出现较严重的洪涝灾害，因此科学确定城市排涝设施的建设标准已成为解决城市暴雨内涝的重要任务之一。设计雨型是制定排水系统设计标准的重要依据和前提，能为城市排水系统的规划和管理、暴雨洪水分析和流域调洪计算提供科学依据[1]。国内的雨型研究开展较晚，以往常用同倍比和同频率雨型，后又引入Keifer和Chu雨型、Pilgrim & Cordery雨型、huff雨型和Yen & Chow雨型[2]，岑国平等[3]对此进行了大量的研究。国外的雨型设计除上述的方法外还有概率密度函数法、随机模型法和离散法等。随机模型法分为单站点模型(如Newman-scott模型和Bartlett-Lewis模型)、多站点模型(如马尔可夫链模型)和时空模型。离散法有级联过程法、混沌过程法和人工神经网络法等[4]。

近年来国内的雨型研究进展缓慢，还是以芝加哥雨型和PC雨型为研究重点，和国外的雨型研究成果相差甚远，进一步深入研究和推进设计雨型工作具有重大意义。因此本文以宿迁市1981-2016年36 a的实测逐时降雨资料为例，在原有设计雨型方法的基础上进行创新，应用同频率法SCS法、暴雨衰减指数法和PDF法来建立宿迁设计雨型，并用Copula函数的风险联合概率将其与同频率雨型进行对比，分析这3种方法应用于宿迁市设计暴雨雨型研究的合理性。

2 设计雨型的研究方法

宿迁地处亚热带和暖温带的过渡地区，主要受北方西风槽、冷涡和热带台风，及当地生成的江淮切变线和气旋等天气系统影响，暴雨主要发生在7-9月份，具有时长、量大、面广的特点，其中特大暴雨会对其城市防洪排涝系统带来巨大挑战。宿迁闸站位于宿迁中心城区边缘，离中心城区最近，是水文部门的国家基础站，其可靠性、一致性和代表性良好。

选取宿迁闸站观测数据，采用年最大值法选取1981-2016年的实测24 h降雨资料，运用下面的4种设计雨型方法推求宿迁市设计暴雨雨型。

2.1 同频率法雨型

同频率法即选取当地实测的典型暴雨，对其降雨过程进行同频率分时段缩放[5]。放大倍比系数公式：

(1)

式中：X设计为不同重现期的设计降雨量，mm；X典型为典型暴雨降雨量，mm。

宿迁市2010年9月7日遭遇特大暴雨，日雨量为历史第二位，达35年一遇，引起巨大的洪涝灾害。该次暴雨雨型为主副型，雨量集中，雨峰偏后，在水文气象特征上具有一定代表性，故选取该特大暴雨过程作为典型暴雨。

采用皮尔逊III型目估适线法[6]计算宿迁市各重现期各时段设计降雨量如表1。

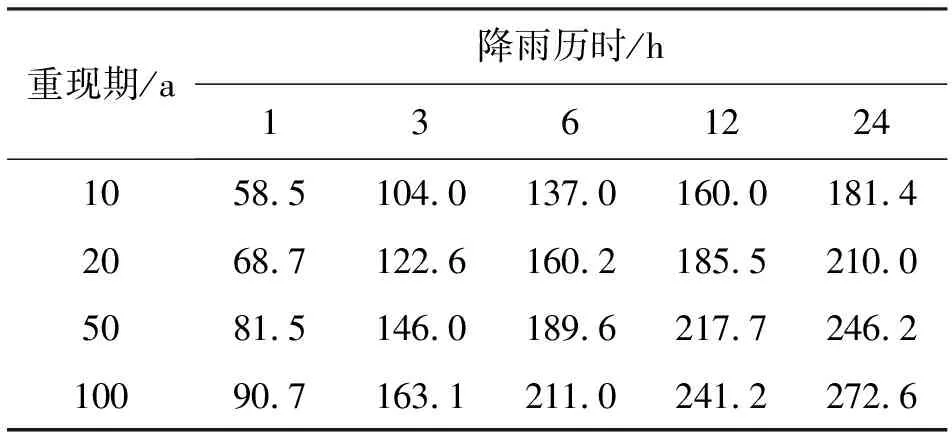
表1 不同重现期下各历时设计降雨量 mm

典型暴雨的最大1、3、6、12和24 h的时段降雨量分别为65.9、147.2、221.1、251.1和256.7 mm，根据公式(1)可计算出各重现期的各时段放大系数，通过缩放典型暴雨过程即得24 h的设计雨型如图1所示。

图1 宿迁市24 h设计雨型(同频率法)

2.2 SCS雨型

SCS雨型是由美国水土局于20世纪80年代建立的，具体分为4种类型。其中SCS-Ⅱ代表由夏季阵雨造成的降雨历时短但强度高的降雨地区，与宿迁市的降雨特征较相似[7]。SCS-Ⅱ雨型的各时段百分比累积数据见表2。

表2 SCS-Ⅱ雨型时程分布数据

由表2各时段累积比例计算降雨时程分配比例，根据宿迁市不同重现期的24h设计雨量可推求出其SCS-Ⅱ设计雨型如图2所示。

图2 宿迁市24 h设计雨型(SCS-Ⅱ法)

2.3 暴雨衰减指数法雨型

宿迁闸站有详细的1、3、6和24 h的降雨系列且属于中小流域，可引入暴雨衰减指数来推求设计雨型[8]。暴雨衰减指数越大表示降雨越集中。由小流域暴雨公式可知，第k时段暴雨量hk为：

(2)

式中：hk为汇流时间(t)内的暴雨量，mm；ik为汇流时间内的暴雨强度，mm/h；H24p为24 h的暴雨量，mm；Bk为暴雨分配系数；np为暴雨衰减系数。

当Bk=1时，反推算汇流时间区间为(t1，t2)的暴雨衰减系数为：

(3)

式中：t1，t2为汇流时间，h；ht1，ht2为对应汇流时间的设计降雨量，mm。

由表1宿迁市的设计雨量，根据式(3)可以计算其暴雨衰减指数如表3。

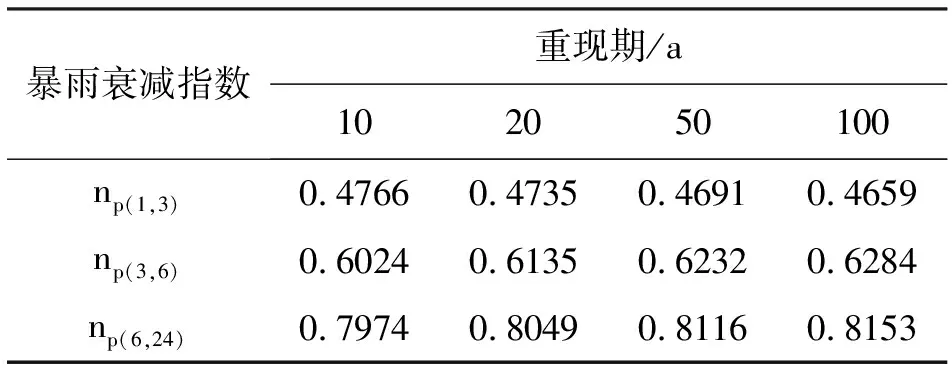
表3 不同时间区间的np值

已知np的前提下，各时段设计雨量可根据以下公式计算[9]：

(1)ti=1～3 h

Hi=H1·ti1-np(1,3)或

Hi=H3·(ti/3)1-np(1,3)

(4)

(2)ti=3～6 h

Hi=H3·(ti/3)1-np(3,6)或

Hi=H6·(ti/6)1-np(3,6)

(5)

(3)ti=6～24 h

Hi=H6·(ti/6)1-np(6,24)或

Hi=H24·(ti/24)1-np(6,24)

(6)

根据《浙江省可能最大暴雨图集》可知，将计算得出的各时段设计雨量的最大值放在峰值位置，次大降雨量放在最大值左边，其余时段雨量从大到小排序，奇数放在左边，偶数放在右边，当一边排满时其余的按从大到小全放到另一边。由宿迁市36 a的24 h的降雨过程计算得雨峰时刻平均值为第10 h，由此得到设计雨型如图3所示。

图3 宿迁市24 h设计雨型(暴雨衰减指数法)

2.4 PDF法雨型

2.4.1 PDF法雨型简介及参数推求 研究得知累积降雨曲线与累积分布函数(CDF)形状相似，而累积分布函数(CDF)的一次微分为概率密度函数(PDF)，因此可用PDF来设计雨型。而且国外已经初步研究了用PDF来构建雨型，结果发现Gumbel、Lognormal和Weibull等概率密度函数可很好的反映降雨过程特征，适用于推求设计雨型[4]。其具体型式如下：

(1)Gumbel分布

(7)

式中：α与β为参数。

(2)Lognormal分布

(8)

式中：η与σ为参数。

(3)Weibull分布

(9)

式中：γ与α为参数。

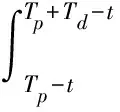
以Gumbel分布为例，公式如下：

Tp=α

(10)

(11)

(12)

参数α，β要同时满足上述的3个目标函数，显然这是一个多元非线性方程组的求解问题，不能直接解出数值，需利用最优化算法进行求解。因此本文采用绝对值求和法，将多目标函数问题转化成单目标函数最优化问题，只要求解出绝对值之和最小时的参数即可，参数结果应满足下式：

(13)

2.4.2 粒子群优化算法 PDF参数求解问题转化成了单目标函数minZ的最优化求解问题。粒子群算法(PSO)算法简单，求解速度快，适合求解实数问题，因此本文采用PSO对函数minZ进行最优化求解，解出Z最小时对应的参数结果。

粒子群优化算法采用速度-位置模型，每个粒子代表着参数解空间的一个，解的好坏程度由适应函数的结果来决定[10]。本文的粒子群算法的学习因子取c1=c2=2。为了使粒子不远离解空间，粒子移动速度应控制在[-vmax，vmax]，一般取vmax=k·vmax，本文取k=0.5。粒子在解空间不断更新迭代直到达到规定的迭代次数或达到规定的误差标准为止[11]。

应用matlab进行粒子群算法编程，以宿迁市2000年的数据为例，计算出Tp、Qp、Qd的输入值，分别用Gumbel、Lognormal和Weibull概率密度函数来拟合2000年实测降雨过程，求解minZ最小，由求解的参数得拟合图如图4所示。

采用粒子群最优化算法分别拟合出每年的Gumbel、Lognormal和Weibull的分布曲线。以宿迁市1981-2016的实测降雨数据为基础进行函数间的拟合优度检验，选择出与实测数据拟合最好的函数。本文拟合优度检验采用3种方法[12]：

(1)拟优平方和准则法

(14)

(2)拟优绝对值准则法

(15)

(3)概率点据相关系数检验法

(16)

式中：x(i)为函数拟合值；y(i)为实测样本值；xm为拟合值的均值；ym为样本值的均值。

由上述公式计算出1981-2016年优度检验均值，结果见表4。拟合优度检验中RMSE和MAE越小越优，PPCC越大越优。对于宿迁市实测数据来说，Gumbel分布是最优分布，可作为其设计雨型。

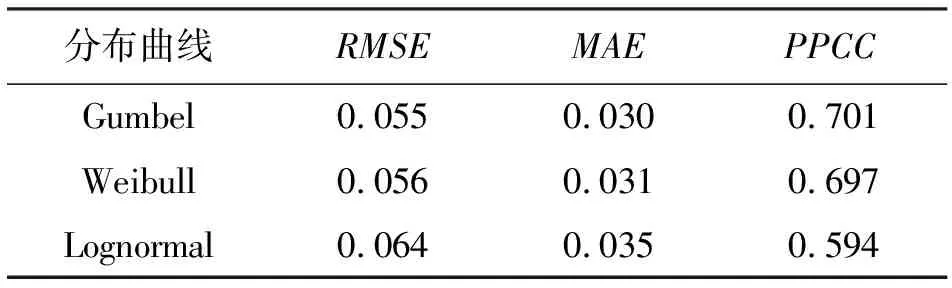
表4 拟合优度检验结果

2.4.3 PDF法设计雨型结果 选用Gumbel分布推求宿迁市设计雨型，由宿迁市36 a的24 h的降雨过程得雨峰时刻平均值为第10 h，即输入值Tp=10。由宿迁市不同重现期下24 h设计雨量和最大1 h设计雨量(如表2)得输入值Qp、Qd。运用粒子群算法计算Gumbel分布参数，得设计雨型如图5所示。

3 基于Copula函数设计雨型的比较分析

不同设计雨型的优劣没有固定的方法来判别，本文尝试利用Copula函数，从设计降雨总量分别与最大1h雨量、最大3h雨量、最大6h雨量间的风险联合分布概率入手，对上述4种雨型进行对比分析。

Copula函数是定义在[0，1]区间均匀分布的联合概率分布函数[13]。由宿迁市36 a实测数据得出变量间为正相关，故本文选取了Gumbel-Hougaard Copula函数来分析设计雨型。GH Copula函数的表达式为：

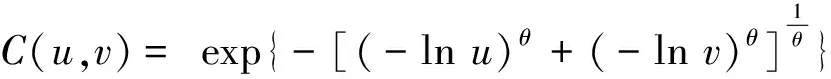
(17)

θ∈[1,∞]

式中：θ为参数。

采用皮尔逊III型来计算边缘分布函数，由矩法得出P-III参数值见表5，通过目估适线法可推求出不同降雨量对应的频率值(即u、v的值)。

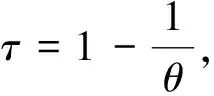
(18)

式中：(xi，yi)、(xj，yj)分别为两组独立同分布的观测数据；sign为符号函数。

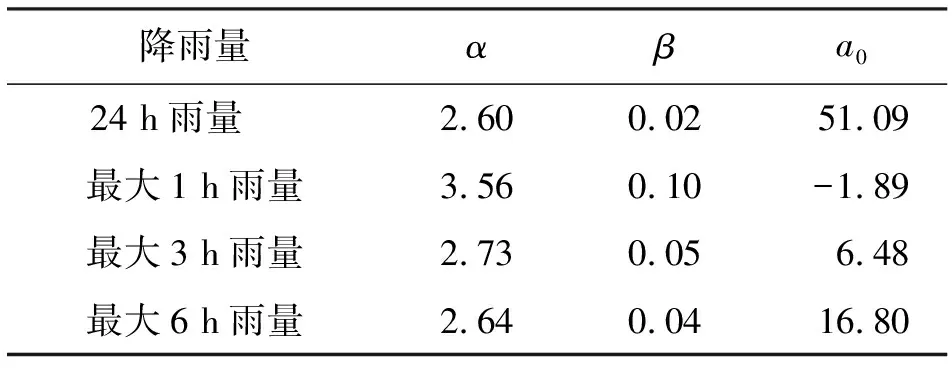
表5 P-III边缘分布函数的参数值

计算得24 h降雨量与最大1、3、6 h降雨量的Kendall秩相关系数τ分别为0.5016、0.5952和0.6302，则对应GH Copula的参数θ分别为2.01、2.47和2.7。

以24 h降雨量与最大1 h降雨量的Copula概率分布关系为例来详细介绍。采用Genest-Rivest法验证理论联合分布函数与经验联合分布函数的拟合程度，结果如图6所示。各点均匀的分布在45°线左右，则GH Copula具有良好的拟合度[15-16]。

本文定义风险率为满足24 h设计降雨量条件下，最大1h(或3、 6 h)降雨量超出对应设计时段降雨量发生的条件概率[5]，计算公式如下式：

(1)

式中：R为24 h设计降雨量，mm；Ri为最大1h(或3、 6 h)时段设计降雨量，mm；F(R)为设计降雨量r的分布函数；F(R，Ri)为(R，Ri)的联合分布函数。

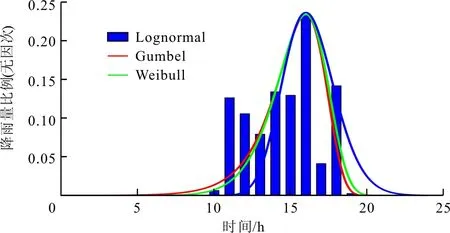
图4 2000年3个分布函数的拟合曲线图

根据GH Copula函数公式可计算出宿迁闸站24 h降雨量与最大1 h降雨量的不同组合下的联合分布概率F(R，Ri)，以此可计算出其风险联合分布概率[17]，结果如图7～8所示。

图5 宿迁市24 h设计雨型(PDF法雨型)

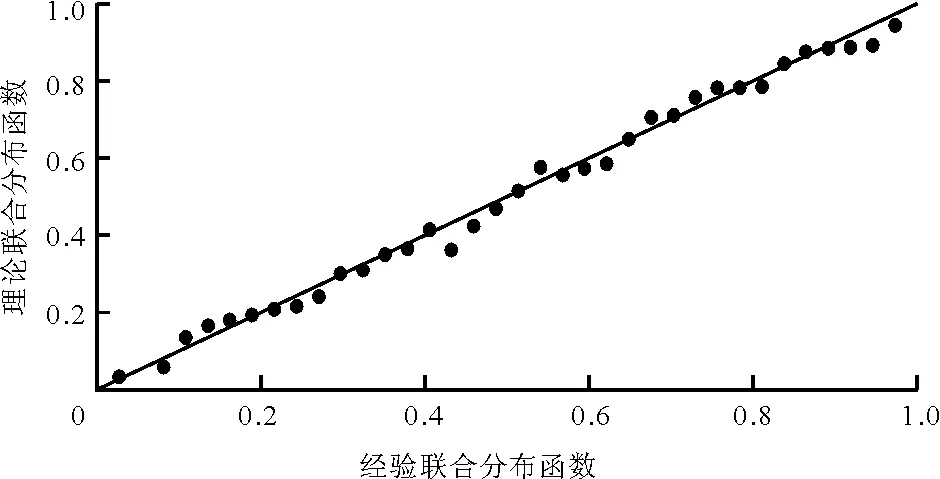
图6 经验联合分布函数与理论联合分布函数

图7 24 h降雨量与最大1h降雨量的联合频率分布图

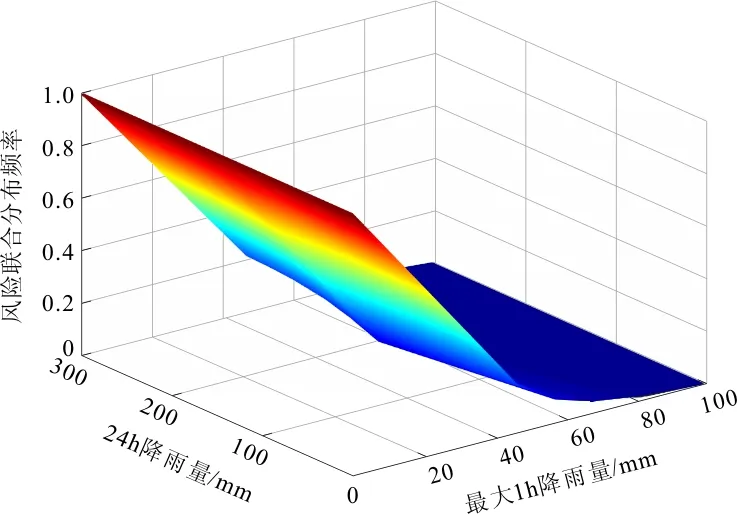
图8 24 h降雨量与最大1h降雨量的风险联合频率分布图

以宿迁市50年一遇的设计雨型为例，计算4种方法雨型的24h降雨量，最大1、3、6 h降雨量，见图7～8，各自的风险联合分布概率，结果见表6。在24 h设计雨量一定的条件下，时段最大降雨量越大，风险联合分布概率越小。

由表6可知：(1)同频率雨型和衰减指数法雨型都以P-III型曲线计算的设计降雨量为基础，风险联合分布概率相同，但同频率雨型雨峰偏后。(2)SCS雨型雨峰较大，24 h与最大1 h对应风险联合分布概率为0.0001(较小)，较安全；24 h与最大6 h的风险联合分布概率为0.010306，表明在最大6 h时段的降雨不太集中。(3)PDF法雨型雨峰与同频率雨型一样，但24 h和最大3、6 h的风险联合分布概率都为0.0000001(最小)，表明最大6 h和最大3 h的降雨较集中，设计雨型偏安全。

表6 50年一遇下4种雨型(风险)联合分布概率

4 结 论

(1)暴雨衰减指数法和同频率法原理相近，是以时段设计雨量为基础来设计雨型；SCS-Ⅱ法是将美国的设计结果运用于宿迁市来设计雨型；PDF法是利用概率密度函数来设计雨型。本文尝试运用该3种新方法推求宿迁市设计雨型，其雨型结果相对于同频率雨型来说整体雨量过程相似，雨量偏差不大，结果合理，因此该方法可为宿迁市雨型的确定提供参考，也能为国内设计雨型的研究发展提供新思路。

(2)从Copula函数中的联合分布概率的思路出发，重新定义风险率，选用GH Copula函数计算风险联合分布概率来进行4种雨型的对比，来分析设计雨型的优劣，Copula函数可以作为雨型对比分析的一种方法。