基于改进凸包算法的树冠轮廓点提取与体积计算

董亚涵，李永强，李鹏鹏，吕亚磊

(河南理工大学 测绘与国土信息工程学院，河南 焦作 454003)

树木作为城市景观中的组成部分，具有重要的生态和环境服务功能，树冠是树木进行光合作用的主要场所，对人类的生活具有重要意义[1,2]。作为树木变化最频繁的部分，树冠的体积是进行树木生长检测和生物量计算研究的重要测量因子，因此树冠体积的测量必须满足一定精度。对于树冠的信息采集，传统方法主要使用围尺、测高仪、测距仪、全站仪等测量仪器对树冠冠幅、树冠高进行测量，但由于传统方法采集的数据不完整，精度不高并不足以对其进行深入分析，而三维激光扫描仪可以高效率、高精度地获取树冠表面的三维点云数据[3-8]。

对于使用点云数据计算树冠体积，常规方法是从点云数据中提取树冠的冠幅、冠高等信息，再将树冠近似为规则几何体，按规则几何体的体积计算公式进行估算树冠体积。但由于树冠结构复杂且不对称，这种方法计算树冠体积易造成较大误差，并不符合精度要求。为此众多学者提出了改进方法，如熊妮娜等将树冠等间距分成多个部分，并将各个部分近似为规则台体，对台体进行体积计算并累加得到树冠体积[9]。韦雪花提出体元模拟法，将树冠点放入体元并设置体元边长阈值，通过计算有效体元数计算树冠体积，经实验证明，当选择的体元边长为1 cm 时，计算出的树冠体积最接近真值[10]，但未考虑到由于树冠遮挡而形成的伪空隙，使用体元模拟法计算的树冠体积往往偏小。樊仲谋利用树冠表面三角网配合立体格网计算树冠体积[11]。巩垠熙等人提出改进的Delaunay算法计算树冠体积[12]。徐伟恒等人通过将树冠等距分层并对每层树冠点云进行投影，再对投影后的点云使用Graham扫描线算法构建凸包多边形[13]，通过多边形构建台体从而得出树冠体积。树冠体积计算的最大问题在于如何精确提取出树冠边缘，并且除掉树冠边缘与树冠间的空隙，传统的凸包算法对提取树冠边缘的精度有限，并且是对分层后的树冠进行整体凸包构建，难以有效地将树冠边缘与树冠间空隙提取出来，本文提出一种改进的凸包算法—迭代渐进的凸包算法，使树冠的提取精度更接近与真实值。

1 迭代渐进的凸包算法

凸包(Convex Hull)作为计算机图形学中的重要概念，已被广泛应用于图像处理、设计自动化、模式识别和运筹学等领域之中。在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包，常用的凸包算法包括穷举法、分治法、JARVIS步进法、Graham扫描线算法、局部凸包算法等[14-19]。由于树冠边缘不规则且树冠内孔隙较多，传统凸包算法无法有效排除树冠空隙，为解决传统凸包算法在提取树冠轮廓点中的不足，本文对传统方法构建的树冠凸包进行了改进，发展了迭代渐进的凸包算法，算法描述如下：

1)将树冠点云自下而上等间距分层，并将每一层点云储存成一个独立单元，分层间距为0.2 m；

2)对分层后的点云进行z轴投影；

3)对每层点云使用传统凸包算法对其进行外层凸包构建，本文中选择的凸包算法为局部凸包算法；

4)设置边长阈值Llimit，对建立的凸包轮廓以每条大于边长阈值Llimit的边为直径作圆形区域，选取圆内的点为疑似边界点，寻找疑似边界点中与直径端点组成最大角的点作为新边界点，从而有效地收缩树冠边界，剔除边界空隙；

5)重复步骤4)进行各条边的运算，直至所有边长都小于边长阈值Llimit，或者以该边为直径的圆内没有点，停止迭代计算。

图1为迭代渐进的凸包算法运算过程，其中(b)为使用传统凸包算法建立的外包围轮廓，并以一条边为直径构建圆，(c)选取圆内黄色的点作为疑似边界点，(d)选择与直径两端点构成最大角的点作为新的边界点。根据三维激光扫描仪采集点云的间隔，本文设置边长阈值为0.1 m 。

2 树冠体积计算

树冠体积计算具体步骤如下：

1)对树冠点进行按高程分层，使用PCL点云库中的欧式聚类算法对分层树冠进行聚类；

2)使用迭代渐近的凸包算法对聚类后的树冠点提取外轮廓并连接选取的轮廓点构成不规则多边形；

3)使用格林公式对建立的多边形进行面积计算。

(1)

式中：S为切片面积，m为单片树冠凸包的总点数，xi为i点的x坐标，yi为i点的y坐标，xi+1为i+1点的x坐标，yi+1为i+1点的y坐标。若树冠分块，则S为各块树冠面积之和。

图2为单株树使用迭代渐进的凸包算法提取轮廓点并构建多边形的结果：(c)(d)(e)为使用迭代渐近的凸包算法对分层点云进行轮廓提取，并通过轮廓点构建不规则多边形。

4)将相邻的两切片构建为多边形不规则台体，通过台体计算式计算单块台体体积并累加，累加结果即为树冠体积。

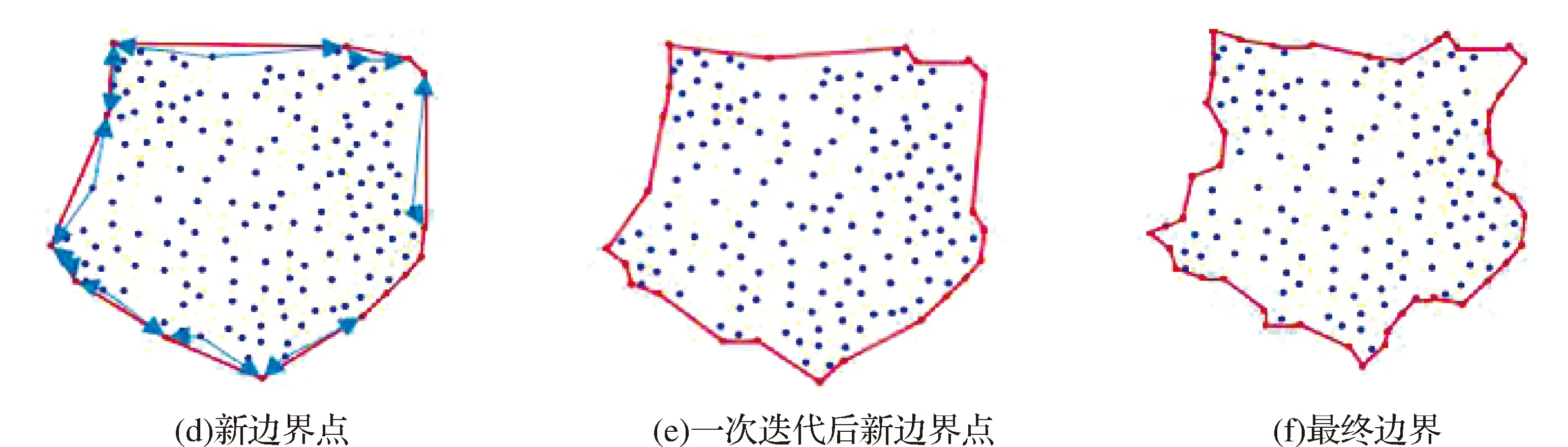
图1 迭代渐进的凸包算法

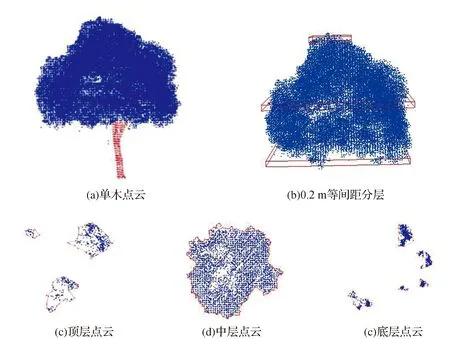
图2 树冠轮廓点提取并构建多边形

(2)

式中：V为树冠体积，n为切片层数，Si为第i层切片多边形面积，Si+1为第i+1层切片多边形面积，h为分层距离[3]。

3 试验分析

为检验上述算法计算出树冠体积的正确性，选取河南理工大学校园内行道树为实验数据，树木种类包括女贞树、柳树等，使用RIEGL VZ-1000型地面三维激光仪对测区树木进行点云数据采集，扫描方式为重复扫描，平均点云密度为3 cm。为获取完整的树种点云，对每一目标树种，均设立3个扫描站，三站位置尽量成120°，以确保树种点云的完整性。数据压缩，点云去噪以及配准拼接等工作均是在配套软件RiscanPro中完成。

从实验数据中选取出树冠形态具有代表性的25株树为样本，对样本进行树冠外轮廓提取与树冠体积计算，选择3种常用且具有代表性的计算树冠体积的方法：几何体模型法、体元模拟法、以及文献[13]中使用Graham扫描线法对树冠进行构建凸包并计算树冠体积的方法，与本文所述方法进行对比，由于树冠的真实体积无法获取，采用人工交互的方法，人为选取外轮廓点，并通过外轮廓点构建多边形以及进行树冠体积计算，将得到的树冠体积作为测量参照值，人工提取虽然并非绝对真值，但由于三维激光扫描仪数据获取精度高，点云密集，人工干预可信程度高，可以作为参考的基准。同时将三种提取树冠外轮廓点的方法置于同一视图中，结果如图3所示。使用迭代渐进的凸包算法自动构建的树冠轮廓与人工提取的树冠轮廓相似度较高。人工提取虽然能够更为精确的提取树冠轮廓，并有效忽略树冠离散点的影响，但人工提取工作量大，提取过程繁琐，工作效率低，不适用于城市中树木的批量处理。

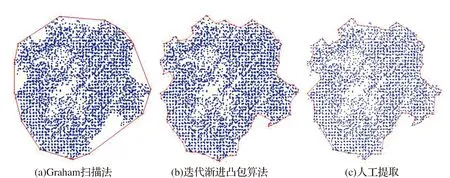
图3 3种树冠外轮廓提取方法对比

将5种方法计算出的树冠体积进行统计，结果如表1所示，其中C1为树冠冠幅，V1，V2为使用几何模型法，体元模拟法计算出的树冠体积，V3，V4为使用Graham扫描线法与迭代渐进的凸包算法构建树冠凸包后计算出的树冠体积，V5为人工交互方式计算出的树冠体积。

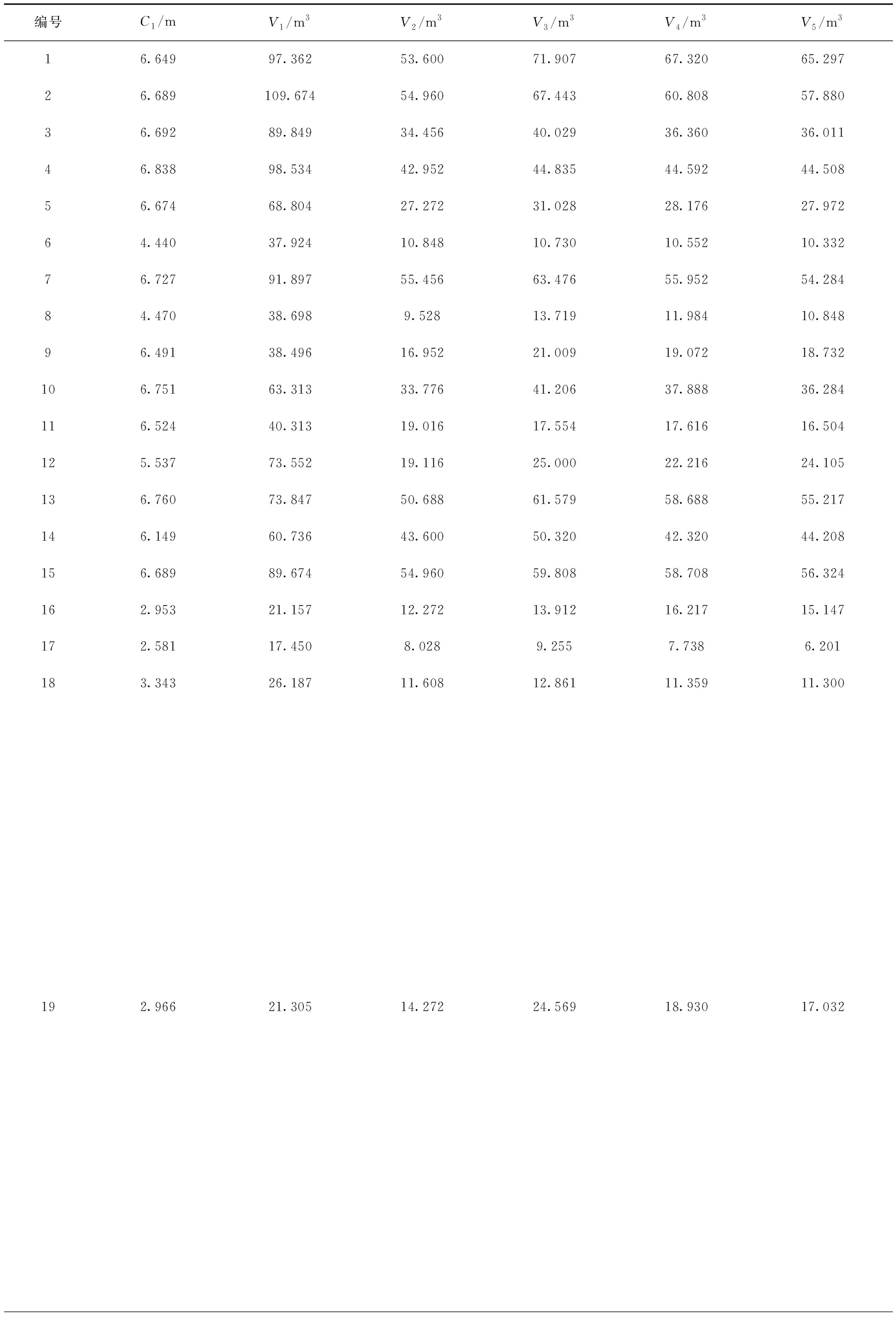
表1 树冠体积计算

续表1

对表1中树冠体积数据进行详细分析，将V5作为树冠的测量参照值，分别计算V5与V1-V4的均方根误差与相关性，结果如表2所示。V4(RMSE=2.342)与V5相关系数r=0.988，说明两组数据高度相关。

表2 V5与V1-V4均方根误差及相关系数对比

将V1～V5放置于同一折线图(图4)中，实验数据表明，除使用几何体模拟法V1(RMSE=47.563)计算结果明显偏大外，另外4种方法计算出的树冠体积相差较小，且V4(RMSE=2.342)结果基本位于V2(RMSE=5.046)，V3(RMSE=6.892)之间，使用几何体模拟法计算树冠体积的方法，只是将树冠模拟为规则几何体，而没有考虑树冠形态的复杂性与树冠空隙，因此计算结果偏大且具有较大误差，体元模拟法计算树冠体积V2，忽略树冠相互遮挡形成的伪空隙，在对树冠边缘格网进行处理后，导致体元模拟法计算出的树冠体积偏小，使用Graham扫描线法V3计算树冠体积，由于未能有效剔除树冠边缘与内部空隙，导致V3计算出的树冠体积偏大，使用迭代渐进的凸包算法有效地减小了树冠边缘与内部空隙对树冠体积的影响，因此V4更接近于树冠体积的真实值V5。

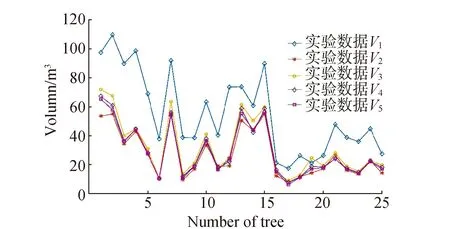
图4 5种树冠体积计算方法结果对比

4 结 论

三维激光扫描系统通过多个方向依次对目标树进行扫描，得到的树冠点云数据完整且最接近于树冠真实形态，通过对树冠进行0.2 m的等距分层并聚类，使用改进的凸包算法—迭代渐进的凸包算法对树冠进行外轮廓点的提取，将提取出的轮廓点构建为不规则多边形，使用格林公式计算每一层多边形面积，并结合台体计算公式最终得到树冠体积。

以25株形态、体积差别较大的树株作为实验对象，由于树冠体积真值无法获取，采用人工交互的方式，人为选取轮廓点，使用选取出的轮廓点计算树冠体积，并以此作为树冠参照对本文算法进行验证，同时将本文方法计算出的树冠体积与几何体模型法、体元模拟法、Graham扫描线法计算的树冠体积进行对比与分析，结果表明，使用迭代渐进的凸包算法计算出的树冠体积(VV4)与几何体模型法(V1)、体元模拟法(V2V)以及Graham扫描线法(VV3)计算出的树冠体积结果相比，与树冠体积参照值(V5)更为相近，相关性更高，并且V4绘制出的体积折线图基本位于V2和V3V之间，也从侧面说明本文所述方法所计算出的树冠体积更接近于树冠真实值。

使用传统测量方法获取树冠的精确信息非常困难，三维激光扫描系统提供了便捷、快速、准确获取树冠表面三维信息的方法，使用迭代渐进的凸包算法对树冠点云进行外轮廓提取，不仅能够对树冠体积进行精细的计算，也为树冠的信息提取与精细自动建模工作提供了基础。本文所述算法更为精确的提取出了树冠的外轮廓点，有效弥补了传统凸包算法应用在树冠外轮廓提取中的不足。

[1] 林树森. 城市增长与城市发展[J]. 城市规划，2011(11): 11-18.

[2] 林树森. 城市道路交通长期规划应突出人居环境理念[J]. 城市与区域规划研究，2015(3): 120-131.

[3] 李杨，李秀峰. 基于点云数据的树木骨架线提取研究[J]. 科技创新与生产力，2017(6)：53-55.

[4] 管西鹏. 树木三维点云数据分析与建模技术研究[D].长沙：中南林业科技大学,2015.

[5] 李宏星，欧阳玉华.基于三维激光扫描点云的树冠面积快速精准计算方法[J].绿色科技，2015(6):72-74.

[6] 梁子瑜.基于TLS点云数据的林分调查因子测定及收获估计[D].南京：南京林业大学，2015.

[7] 王祺，胡洪，吴艳兰，等. 基于点云数据的树冠体积自动求算方法[J]. 西北林学院学报,2017,32(2):242-246.

[8] 臧克. 基于Riegl三维激光扫描仪扫描数据的初步研究[J]. 首都师范大学学报(自然科学版)，2007，28(1)：77-82.

[9] 熊妮娜，王佳，罗旭，等. 一种基于三维激光扫描系统测量树冠体积方法的研究——以油松为例[J]. 北京林业大学学报，2007(增2)：61-65.

[10] 韦雪花，王永国，郑君，等. 基于三维激光扫描点云的树冠体积计算方法[J]. 农业机械学报，2013(7): 235-240.

[11] 樊仲谋，冯仲科，郑君，等. 基于立方体格网法的树冠体积计算与预估模型建立[J]. 农业机械学报，2015(3)：320-327.

[12] 巩垠熙，何诚，冯仲科，等. 基于改进Delaunay算法的树冠三维重构单木因子提取[J]. 农业机械学报，2013(2): 192-199.

[13] 徐伟恒，冯仲科，苏志芳，等. 一种基于三维激光点云数据的单木树冠投影面积和树冠体积自动提取算法[J]. 光谱学与光谱分析，2014(2): 465-471.

[14] 张飞，谢步瀛，闫星宇，等. 改进的三维点集凸包求取算法[J]. 计算机辅助工程，2009, 18(1): 78-82.

[15] 黄俊杰，罗周全，秦亚光，等. 复杂采空区三维散乱点建模技术研究及应用[J]. 东北大学学报(自然科学版)，2016，37(12)：1784-1788.

[16] 吴文周，李利番，王结臣. 平面点集凸包Graham算法的改进[J]. 测绘科学，2010(6): 123-125.

[17] 蒋联源. 凸壳算法及其应用研究[D]. 南京：广西师范大学，2007.

[18] 李必栋，闫浩文，王中辉，等. 坐标排序的离散点凸包生成算法[J].测绘科学，2017，42(2):14-17.

[19] 黄先锋，程晓光，张帆，等. 基于边长比约束的离散点准确边界追踪算法[J]. 武汉大学学报(信息科学版)，2009(6): 688-691.