基于高低帽变换的图像迭代分割方法

2018-07-21阳振宇潘建平

测绘工程 2018年8期

阳振宇,潘建平,陈梦

(1.重庆交通大学,重庆 400074;2.山东科技大学,山东青岛 266590)

图像分割是图像识别和分析的基础，是图像处理中的一项首先需要解决的问题，其目的是将图像中的目标区域突显出来，为后续的处理提供便利。阈值分割是一种基于强度的分割方法，它是根据像素分布(即直方图)来工作的，根据选取阈值的大小以及个数将图像分成两个或多个有意义的部分[1]，属于同一部分的像素被认为是同一个物体，其算法具有简洁迅速的特点，能满足系统快速响应的要求。

阈值分割的一个难点在于如何选取一个合适的阈值对图像进行分割，阈值的选取直接影响图像分割的效果[2]。经过国内外大量的研究，提出最大熵法、迭代法、大津法等不同阈值自动选取方法。这些方法中，迭代法是一种应用范围较广的方法，其核心思想是步步迭代逼近。王正[3]通过迭代阈值算法分割垩白大米，但由于垩白大米的垩白部分和正常部分图像区别度较大所以能取得较好的效果；张长胜[4]等人对otsu算法选取阈值的缺陷进行改进，将整体阈值再区分并结合离差平方和作为适应度函数选取最佳阈值来分割压力表盘图像，提高目标图像的阈值分割效果，但是压力表盘属于特殊目标，不能扩展应用到其他对象上；王富治[5]等人对传统典型的PCNN网络进行改进，去掉一些次要参数，突出灰度对分割的影响，根据灰度特性分两阶段迭代分割，错分概率大大减小，但是该方法仅限于实验阶段，无法针对某一实际问题进行应用；杨帆[6]等人在对印刷电路板图像的分割中采用改进的遗传算法来确定初始分割的最优化阈值，再将这个最优阈值应用到二维最大类间方差法快速迭代中来获得最优解，分割较为清晰，降低错分率，但是算法较为复杂，对于照片的采集过程的光线控制较为严格；陶士凤[7]等人通过将Canny算子与迭代法相结合最后通过小波融合来互补以上两种方法的不足，但同样该方法是以时间复杂度为代价，并不利于实时性的处理且对于工程应用来说还有一定距离；莫胜撼[8]等人在迭代法中通过每次迭代后，重新划分分割值的选择范围，并在该范围内进行搜索，迭代收敛速度更快，但是该算法以牺牲精度来换取速度。现有的这些算法中，绝大多数都是针对医学图像和工业图像进行操作，应用范围具有一定的局限性，还没有针对工程领域的一些有效算法，同时对于图像分割的精度和效率方面还有一定的提升空间。

针对上述问题并结合工程实际应用，本文提出一种基于高低帽变换的迭代分割算法，通过高低帽变换提升图像的动态灰度范围，降低工程实际中对于原始图像获取的苛刻条件，再通过迭代法分割出目标区域，在分割效率和精度上都能得到很好的保证。

1 数学形态学与高低帽变换

1.1 数学形态学

数学形态学是一种建立在微分几何、集合论和网格代数基础上的一门学科。其基本代数算子有4个：膨胀运算、腐蚀运算、开运算、闭运算，它们在二值图像和灰度图像中有着不同的特点。通过这些基本的运算，还可以推导组成各种不同用途的实用算法，用它们对图像进行分析处理，算法具有运算速度快、简洁、可并行处理等特点。数学形态学核心思想是利用一个“探针”即结构元素去探索图像信息，“探针”本身直接携带一些先验知识(形态、大小)，通过结构元素在图像中的不断移动来考察图像中各个部位之间的相互关系[9]。

现就形态学基本算子进行介绍，设f是输入图像，b是结构元素，Df和Db分别是f和b的定义域，则：

1) 膨胀运算：

(f⊕b)(s,t)=max{f(s-x,t-y)+

b(x,y)|(s-x),(t-y)∈Df;(x,y)∈Db}；

(1)

2) 腐蚀运算：

(fΘb)(s,t)=min{f(s+x,t+y)+

b(x,y)|(s+x),(t+y)∈Df;(x,y)∈Db}；

(2)

3) 开运算：

fob=(fΘb)⊕b；

(3)

4) 闭运算：

f·b=(f⊕b)Θb.

(4)

膨胀运算可以与目标区域接触的背景点合并到该目标区域中，使目标边界向外部扩张处理，通常用来填补目标区域的某些空洞以及消除包含在目标区域的细小噪声；腐蚀是一种消除边界点，使边界向内部收缩的过程，可以用来消除小且无意义的目标；开运算则用来消除细小物体，在纤细点处分离物体和平滑物体边界时又不明显改变其面积；闭运算用于填充物体内细小的空洞，连接相邻物体，在不明显改变物体面积的情况下平滑其边界[10]。

1.2 高低帽变换

高低帽变换是由上面几种算子组合而来，高帽(top-hat)变换是将原始图像与图像的开运算做差，因其结构元素形似一顶高帽而得名，低帽(bottom-hat)变换是图像的闭运算结果与原始图像做差而来，其定义如下：

1)高帽变换：

That(f)=f-fob；

(5)

2)低帽变换：

Bhat(f)=(f·b)-f.

(6)

高帽变换的一个重要用途是对不均匀光照的图像进行校正，而低帽变换正好相反。因此使用高低帽变换可以对图像进行增强，高帽变换具有高通滤波的一些性质，可以突出图像细节，而低帽变换具有低通滤波的特点，突出相连接目标间的界限，高低帽变换结合使用可以将图像的目标与背景得到拉伸，突出目标与细节信息。在原始图像上加上高帽变换的结果再减去低帽变换可以有效的提高图像对比度。

2 改进的迭代分割算法

在一幅图像中目标与背景之所以能够区分开是因为它们的灰度值不一样，目标物体的灰度值大于或小于周围背景的灰度值。当一幅图像质量较高，对比度较大时，目标与背景的差异在直方图上表现为两个峰值：一个是目标，一个是背景；然而当图像对比度较低且存在噪声干扰时，这种差异则无法在直方图上得到体现，但是在局部区域上目标与背景仍有差异。迭代法阈值分割对整幅图使用一个阈值，即对于一幅图采用一个背景亮度，不能正确处理局部区域的灰度差异导致误分割。

针对一般迭代法的不足之处，本文提出先对原始图像进行高低帽变换增强对比度[11]，拉伸图像的灰度动态范围同时锐化图像使图像清晰，然后再通过迭代找出阈值进行分割，针对一些较为复杂的图像可再次采用低帽变换凸显目标区域，最后通过二值图像连通域标记，按面积擦除噪声完成分割。

2.1 结构元素的选取

在形态学运算中结构元素的选取非常重要，其尺寸和形状直接影响到处理结果，构造不同的结构元素可以得到不同的效果，完成不同的图像分析。结构元素的选取应根据处理目的以及原始图像进行，一般来说其几何形状应该比原始图像简单，并且存在边界。结构元素的选取非常灵活，常用的形状包括圆形、正方形、菱形、十字形、六边形、直线形等，甚至可以是根据需要设置的任意形状，如果结构元素各向同性，可以得到与方向无关的运算结果。由于菱形结构元素具有高度的对称性，因此本文选择菱形结构元素。确定结构元素的形状后，其尺寸就至关重要。小尺度的结构元素对于噪声抵抗能力弱，但是可以较好的保留边缘细节信息；大尺度的结构元素抗噪能力突出，但是对于边缘有一定的模糊，综合取舍，本文选择15像素×15像素的大小。

2.2 算法及实验步骤

1) 结构元素采取上文所述的15像素×15像素的菱形结构元素；

2) 用数学形态学高低帽变换提升图像灰度范围，凸显目标区域，即：

f1=f+That(f)-Bhat(f).

(7)

3) 将处理后的图像进行灰度化操作，求出图像的最大灰度值和最小灰度值分别记为zmax，zmin，令初始阈值

T0=(zmax+zmin)/2.

(8)

4) 根据初始阈值分割结果，分别求出新图像的背景和目标的灰度平均值，记为zo,zB，求出新阈值

T=(zo+zB)/2.

(9)

5) 若两个平均灰度值zo,zB的变化小于给定阈值，则停止迭代，否则返回(4)；

6) 将分割的图像进行连通域标记，按面积擦除噪声，在本工程实际中对噪声估计通过反复的实验确定，本文阈值选为25和95。

3 实验结果及分析

本文所采用的图像均来自某一桥梁自动化检测所采集的数据，原始数据如图1所示。由于受到周围环境的影响和设备的限制采集到的图像上还是存在较多干扰。为验证算法的有效性，现针对桥梁主要承载结构桥面以及桥梁拉索进行分析，这几幅图像具有典型的桥梁结构图像的复杂特性，背景不均一，存在噪声污染，信息量分散，目标区域不规则，而且还存在光照不均的现象。采用常规的分割方法难以得到满意的检测结果。本实验在MATLAB2014a平台上进行操作。

图2(a)是一幅桥面的裂缝图像，图像包含大量的裂缝信息，而且还存在一些不规则的细小空洞凹陷，现使用迭代法对其进行阈值分割，结果如图2(b)所示。绝大部分的裂缝被分割出来，但是针对图像中1，2号区域中所包含的细小空洞在分割图上并不能得到很好的体现，完全被淹没在“雪花”状噪声中；同时对于3号区域中的细小裂缝，由于噪声的干扰，识别也是相当困难，分割精度极低，完全达不到后续处理的要求。

导致这种结果的原因在于原图像的背景亮度不均一，对比度不大，不能使用一个阈值来划分整幅图。如果能提高图像的对比度，使图像背景均匀，那么分割正确率会大大提升。要想使图像变得均匀，可以通过高低帽变换来实现。

同样针对图1(a)的原始图像，首先分别对原始图像进行高帽变换和低帽变换，然后将高帽变换的结果减去低帽变换的结果后叠加到原始图像上，这样可以提高图像的对比度，达到图像增强的目的，结果如图3(b)所示。增强后的图像仍然是彩色图像，因此需要将图像进行灰度化处理；灰度化后为了进一步提高图像的对比度，采用二次低帽变换来处理，突显出细节，便于分割，如图3(c)所示，最后采用迭代法分割即可。在这个过程中，虽然图像细节被一次次放大，对比度得到加强，但是不可避免的造成一些噪声的加强，鉴于此，通过对二值图像进行区域标记对连通域进行面积计算，去除小于阈值面积的连通域，即进行面积剔除，去除明显干扰，然后进行形态学处理连接破碎裂缝，从实验中可以看出处理效果良好，针对1、2号细小空洞区域，对于噪声进行极大抑制，空洞信息得到凸显，能较好的还原桥面真实情况；同时对于3号区域中细小的裂缝通过对噪声的滤除也能得到很好的保留，对于原图像中裂缝的走向都能较好的提取到，可以看出本文算法的抗噪声能力较强，分割精度得到显著提高。仿真效果如图3(d)所示。

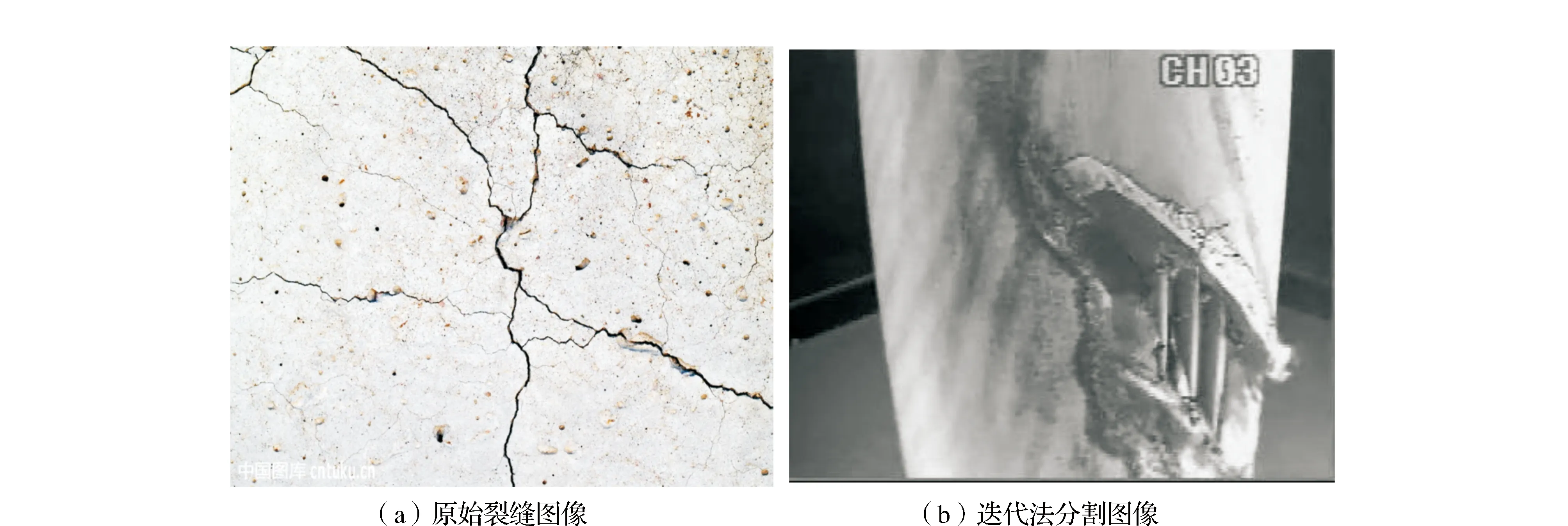
图1 原始数据图

图2 桥面裂缝分割图

图3 桥面裂缝本文算法分割图

对于以上背景不均一的小目标区域，经过本文改进的算法分割能得到较好的效果，如果目标区域物体较大，同样可采用上述思路分割。如图4所示，图4(a)为采集的某一桥梁拉索缺陷图片，中间区域是明显的破损区域，需要提取出来做进一步的分析。直接用迭代分割得到的图像如图4(b)所示，对于缺陷区域有明显的误分割，图4(a)中1号区域在原图中可以明显看出是拉索磨损疲劳后褶皱引起的颜色变化，并不是破损病害，但是却被误分；同样3号区域也只不过是拉索本身的纹理而已，也被分割进了目标区域；在真正破损的2号区域中，目标区域被笼统的分割在一起，细节信息丢失严重，目标边缘更是无法分辨，增加缺陷区域的外延，对于后续判断造成极大的干扰；同时对于4号区域明显不属于拉索主体结构，但是也被分割成拉索的一部分，这是绝不允许的。

通过本文改进的迭代分割算法进行处理后，如图4(c)所示，可以看出破损区域基本被完整保留下来。对于1号区域拉索颜色的变化能够正确识别，不存在误分；同时针对2号区域的关键破损位置，对内部较小较为离散的目标都能得到分割，细节信息保持得很完整，最关键的是对于整个破损区域的边缘都得到较好的保存，正确标识目标区域的轮廓；3号区域的纹理也能正确区分开，并没有纳入目标区域；同时对于4号区域明显的非拉索结构也没有并入拉索主体中；总体来说分割出的目标更接近于实际，且不存在过度分割的现象，背景与目标得到有效的区分，能较好的分割出目标。

同时对比处理这些图像所获得的最佳阈值和时间复杂度，如表1所示，可以看出，本文所提出的算法在时间复杂度上有些许提升，但是对于分割的阈值是较为精确的，在效率和精度上能达到很好的统一，在实际工程中也能满足系统快速响应的需求。表2给出对于改进算法的客观评价结果。其中峰值信噪比是一种对于图像质量最为普遍和使用最广的客观量测法，其值越大代表失真越少；模糊系数则可以用来评价一幅图像信息量的大小，其值越大表明图像越模糊，分割效果越差，本文改进后的算法能较好地提高图像的质量，保留图像的原始信息。