角接触球轴承非线性动态特性分析
2018-07-21姚建涛于清焕孙晓宇李双凤王振
姚建涛,于清焕,孙晓宇,李双凤,王振
(1.燕山大学 河北省并联机器人与机电系统实验室,河北 秦皇岛 066004;2.东北大学 机械可靠性与动力学研究中心,沈阳 110819;3.瓦房店轴承集团 精密转盘轴承有限责任公司,辽宁 大连 116300)
空间轴承作为航天机构中旋转关节的最基本组成部分,合适的预紧力可以提高支承刚度和旋转精度[1]。预紧力较小时,系统工作精度无法保证,在高速或重载下轴承易出现振动现象;预紧力较大时,摩擦力矩变大,易出现卡滞现象,摩擦热导致轴承温度升高,降低使用寿命。在航天机构及精密机械中,轴承安装时预紧力必须合适,且需精确确定[2]。
输出轴系作为航天机构的重要组成部分,轴系中轴承安装配合过盈量和预紧力的选择成为研究的重点和亟须解决的问题。文献[3]在考虑轴系材料属性、轴承排列方式和预紧方式的基础上,利用材料热变形和位移变形协调关系,建立轴承径向游隙与预紧力随交变温度变化的数学模型。文献[4]提出一种涉及轴承游隙与柔性特征影响的多体系统建模方法,采用力约束替代运动约束,构建多体系统环境下的轴承精细化模型。文献[5]提出材料热特性轴承预紧力自动调节方法,该方法是根据温度变化时金属材料受热伸长的特性,通过分析机床主轴转速上升时摩擦功率损耗产生的热量,建立主轴温度场模型。文献[6]用计算机辅助设计软件绘制出轴承安全区域图,并绘制出径向游隙与轴向位移之间的变化关系图,确定出相对位置,求出轴系的各待定参数,完成轴系分析与设计。文献[7]基于Hertz接触理论和接触变形协调关系,分析了径向游隙、表面粗糙度、载荷和球数对轴承非线性动力学性能的影响。
上述研究主要集中在安装配合过盈量对轴承动力学性能和稳定性影响2个方面,关于预紧力对轴承的非线性动态特性的影响的研究较少。根据集中质量法,建立考虑球数、轴向预紧量和动载荷的角接触球轴承力学模型,推导出轴承非线性动力学微分方程组,并对方程组进行坐标变换,然后进行量纲一化处理,利用数值分析软件求解非线性微分方程组得到轴承的相图和Poincane图,并分析轴向预紧量、接触角对轴承非线性动态特性的影响。
1 建立动力学模型
轴承安装配合示意图如图1所示,由2套角接触球轴承背对背安装,轴承中间安装有隔套,由锁紧螺母实现轴承轴向定位预紧。轴承运行过程中主要承受轴向和径向载荷,外圈固定,内圈旋转,建立单套轴承非线性动力学模型如图2所示。Oxy为绝对坐标系,x,y方向分别为轴承内圈平移方向;Ojxjyj为相对坐标系,xj,yj方向分别为球平移方向(j代表第j个球);φj为第j个球中心与坐标原点O的连线与x轴的夹角。
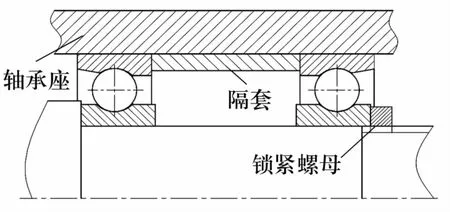
图1 安装配合示意图Fig.1 Diagram of installation and match

图2 动力学模型图Fig.2 Diagram of dynamic model
由图2中各零件之间的相对位置关系可知,轴向预紧量δz与接触点变形δ之间的关系为

轴旋转时,第j个球与内圈在接触点处的相对位移为

式中:ω为球公转速度;t为时间;Z为球数;α为接触角。
第j个球与外圈在接触点处的相对位移为
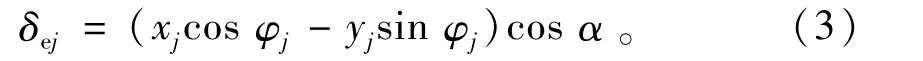
由球与内、外圈之间的相对位移关系,并根据牛顿第二定律,建立轴承系统的非线性动力学微分方程组为


2 参数影响分析
2.1 轴承参数
所分析轴承基本参数见表1,轴承转速为1.1 rad/s,径向无载荷,轴向载荷根据预紧量确定,采用MATLAB中ode45命令对(7)式进行求解。
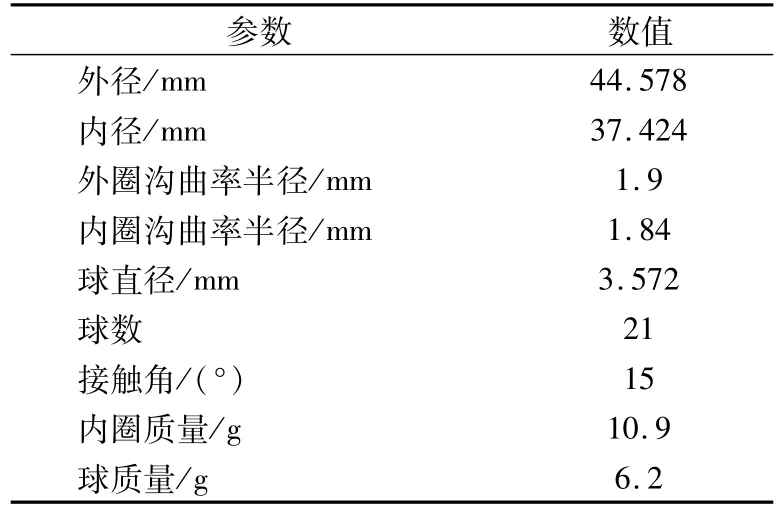
表1 结构参数Tab.1 Structural Parameters
2.2 轴向预紧量影响分析
轴向预紧量δz=0.4μm时,轴承相图如图3a所示,Poincane图如图3b所示。图中,dμ1n为量纲一的速度,μ1n为量纲一的位移。轴承相图轨迹混乱、无序,且是不随时间呈周期性变化的封闭曲线,Poincane图中包含较多无规律离散点,散乱分布且不重复,轴承处于典型的混沌运动状态。

图3 δz=0.4μm时轴承振动特性Fig.3 Vibration characteristics of bearing when δz=0.4μm
轴向预紧量δz=1.9μm时,轴承相图如图4a所示,Poincane图如图4b所示,相图轨迹为不规则形状封闭曲线,Poincane映射图为一条闭轨迹环,表明轴承处于典型准周期运动状态。轴向预紧量δz=4.4,7.2,16.0,24.0μm时,轴承相图、Poincane图分别如图5—图8所示。相图为一条封闭曲线,周期轨迹在穿越Poincane截面时为有限个不动点,表明轴承处于周期运动状态。轴向预紧量变化时,μ1n始终大于0,表明球与内圈接触,不存在碰撞的情况。
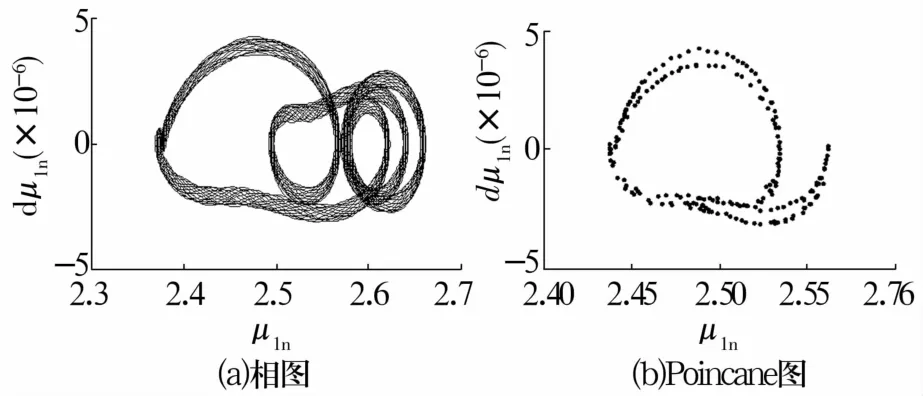
图4 δz=1.9μm时轴承振动特性Fig.4 Vibration characteristics of bearing when δz=1.9μm
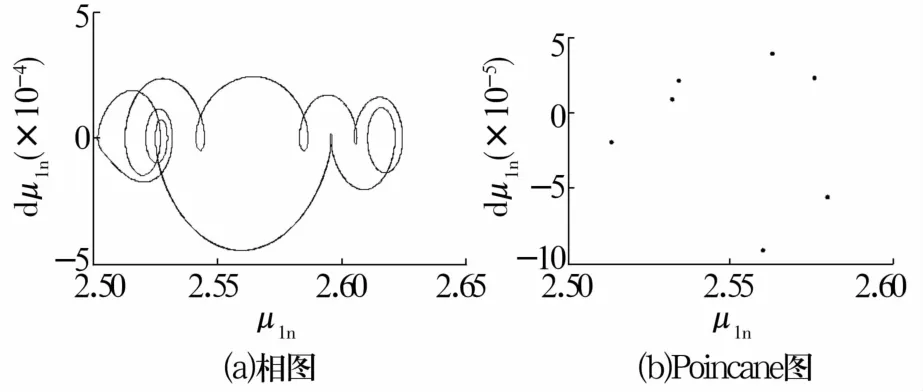
图5 δz=4.4μm时轴承振动特性Fig.5 Vibration characteristics of bearing when δz=4.4μm
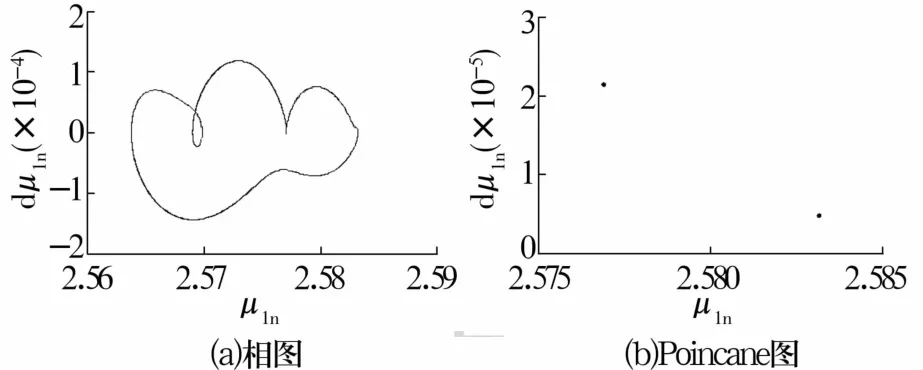
图7 δz=16.0μm时轴承振动特性Fig.7 Vibration characteristics of bearing when δz=16.0μm
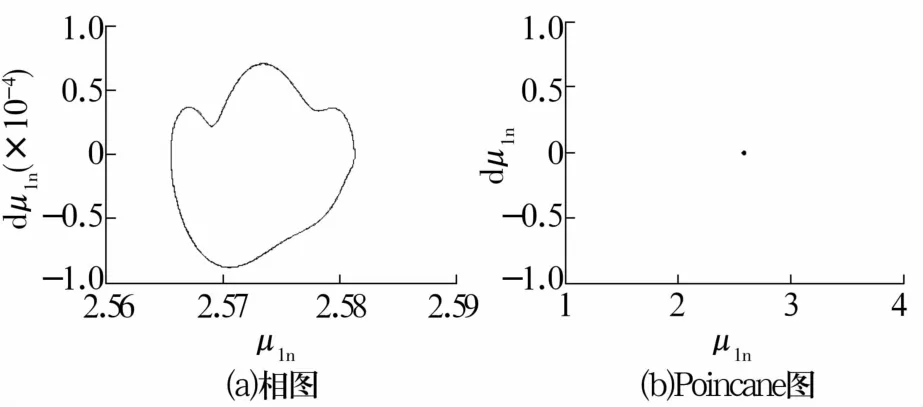
图8 δz=24.0μm时轴承振动特性Fig.8 Vibration characteristics of bearing when δz=24.0μm
轴向预紧量逐渐减小时,轴承由稳定的单周期运动状态经倍周期分叉进入多周期运动状态,然后进入准周期运动状态,最后进入混沌运动状态。轴向预紧量较小时,球与内圈窜动量大,会使轴承处于不稳定状态。因此,增加轴向预紧力能增加轴承的运动稳定性。但过大的轴向预紧力会降低轴承的传动效率,增加轴承的磨损,应在满足轴承运动稳定性的条件下,选择较小的轴向预紧力。
2.3 接触角影响分析
δz=15.0μm时,改变接触角α,得到处于不同运动状态的轴承相图和Poincane图。接触角α分别为 15°,20°,25°时,得到相图 Poincane图分别如图9—图11所示。相图均为一条封闭曲线,周期轨迹在穿越Poincane截面时为有限个不动点,表明轴承处于周期运动状态。接触角增加时,球与内圈接触,无碰撞发生。接触角α=30°时,轴承振动特性如图12所示,相轨迹为不规则形状封闭曲线,Poincane映射图呈现一定的规律,表明轴承处于典型准周期运动状态。接触角α=35°时,由轴承振动特性图(图13)可知,轴承处于典型混沌运动状态。
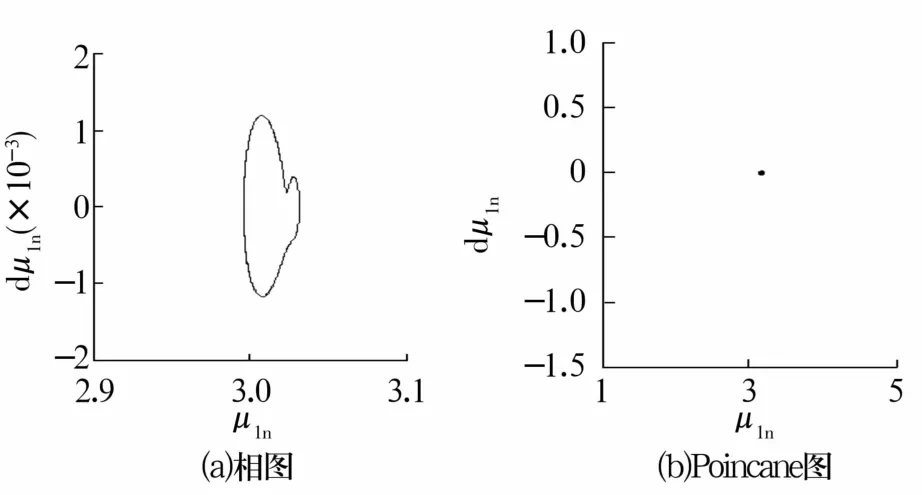
图9 α=15°时轴承振动特性Fig.9 Vibration characteristics of bearing when α=15°
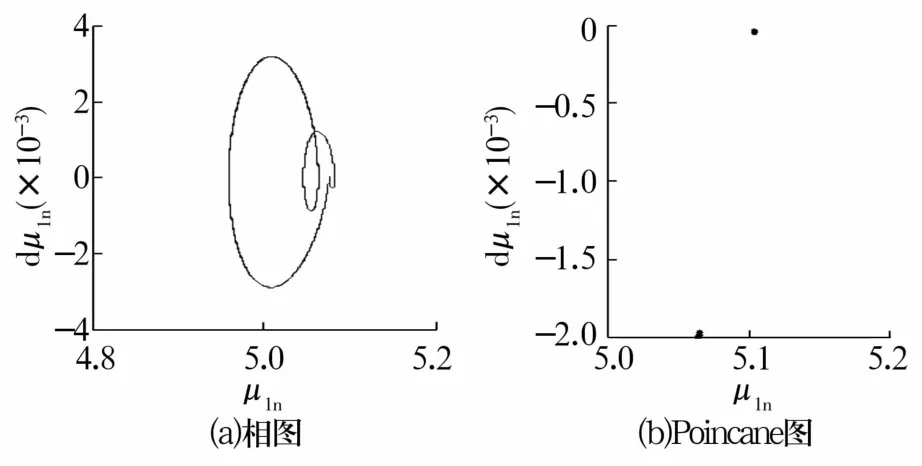
图10 α=20°时轴承振动特性Fig.10 Vibration characteristics of bearing when α=20°

图11 α=25°时轴承振动特性Fig.11 Vibration characteristics of bearing when α=25°

图12 α=30°时轴承振动特性Fig.12 Vibration characteristics of bearing when α=30°
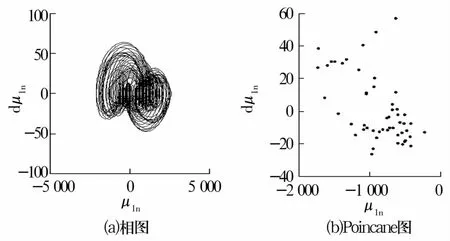
图13 α=35°时轴承振动特性Fig.13 Vibration characteristics of bearing when α=35°
接触角增加时,轴承由稳定的单周期运动状态经倍周期分叉进入多周期运动状态,然后经过Naimark-sacker分叉,经过不稳定吸引子最终进入混沌运动状态。接触角较大时,球与轴承内圈发生相互碰撞,轴承处于不稳定状态。较大的接触角会降低轴承径向承载能力,并影响轴承的传动平稳性,故应选择较小的接触角。
3 结论
根据角接触球轴承动力学模型,建立轴承的非线性动力学微分方程组,并对其非线性动力学特性进行分析,得到如下结论:
1)增加轴向预紧量,能够减小轴承的振动响应幅值,提高轴承的运动稳定性。随轴向预紧量减小,轴承响应幅值逐渐变大,并由单周期运动经倍周期分叉进入多周期运动,然后经准周期运动进入混沌运动。在满足轴承运动稳定性的条件下,为保证轴承的使用寿命和轴承的传递效率,应选择较小的轴向预紧力。
2)增加接触角,轴承的振动响应幅值增加,轴承的运动稳定性降低。随接触角增加,轴承响应幅值逐渐变大,并由单周期运动经倍周期分叉进入多周期运动,然后经过不稳定吸引子最终进入混沌运动状态。为保证轴承的传动平稳性,应选择较小接触角。
