韦达定理的风采

（云南省玉溪市教育科研究所 云南玉溪 653100）

中学学习的韦达定理，在今后的数学学习中一直都起着很重要的作用，它在中学阶段的学习和考题中都是重点内容，因此，对此定理要给以重视，要学好用好。下面看看韦达定理与其它知识的合作风采。

一、韦达定理与中点坐标公式联袂合作

（Ⅰ）证明：抛物线C在N处的切线与AB平行；

（Ⅱ）是否存在实数k使若存在，求k的值;若不存在，请说明理由。

[解析]（Ⅰ）设A（x1，2x12），B（x2，2x22），

[评析]在解题过程中，若涉及到直线与圆锥曲线，线段的中点时，一般就用韦达定理和线段的中点坐标公式来求解。

[评析] 一般地，解含常数的一元二次方程时，常设出方程的两根，通过整体代换得到需要的答案，而其两根不需要求出，即设而不求。

二、韦达定理与弦长公式亲密联合

（Ⅰ）证明抛物线C在N处的切线与AB平行；

[解析]（Ⅱ）设A（x1，2x12），B（x2，2x22），由（Ⅰ）得，

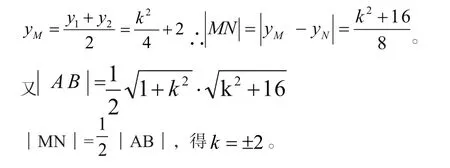
[评析]在与圆锥曲线题目里，遇到线段时，常用韦达定理和弦长公式联合解决问题。

三、韦达定理与垂直向量的交汇

例4.（2008·辽宁卷）在平面直角坐标系xoy中，点P到两点的距离之和等于4，设点P的轨迹为C，直线与C交于A、B两点。

（Ⅰ）求C的方程；

[解析]（Ⅰ）设P（x，y），A（x1，y1），B（x2，y2），

四、韦达定理与数列的协调对接

例5.（2008·全国I卷）双曲线的中心为原点O，焦点在x轴上，两条渐近线分别是，经过右焦点F垂直于的直线分别交于A、B点。已知成等差数列，且与同向。

（Ⅰ）求双曲线的离心率；

（Ⅱ）设AB被双曲线截得的线段长为4，求双曲线的方程。

[评析]该题目里给出了直线与圆锥曲线相交所成线段的等量关系，需按题意列出等式，代入韦达定理对应的代数式，解出参数的值，则可得到题目所要的答案。

韦达定理在解析几何的解题中应用比较广泛，其算理简单，算法单一，只需在化简计算时仔细认真点，则可轻松拿到解析几何的高分。