核心素养视角下空间观念的培养策略

曾华静

[摘要]“核心素养”是近年来教育界的热门话题之一。高中数学率先提出六大核心素养：数学抽象、直观想象、逻辑推理、数学运算、数学建模、数据分析。小学阶段并没有对数学核心素养有一个明确的界定，但是许多小学教师对照高中数学的核心素养，找到与之相对应的核心词，如数感、符号意识与高中数学抽象相对应；空间观念、几何直观与高中数学直观想象相对应；推理能力与高中数学逻辑推理相对应；运算能力与高中数学运算相对应等。本文着重探讨了小学生空间观念的培养问题，以此深化小学生核心素养的培养。

[关键词]核心素养；空间观念；知识建构；数学思维

空间观念的培养是数学核心素养的重要内容之一。什么是空间观念？2011版课标明确指出：空间观念主要指根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体；想象出物体的方位和相互之间的位置关系；描述图形的运动和变化；依据语言的描述画出图形等。在培养空间观念的教学中，教师可以尝试从图形的认识、度量、变换和位置关系中，通过一系列的直观手段和空间想象，让学生看得见、悟得来。

一、在观察中形成知觉，再现几何图形

观察是有目的、有计划、比较持久的知觉，它是学生认识几何图形，获取图形特征的重要途径。小学数学课堂教学活动过程中的观察，可以把几何图形的个别属性联系起来，使学生在大脑中产生对图形的整体感知，对几何图形形成更鲜明、更生动、更具体的感性知觉，达到初步认识几何图形的教学目的。

例1：二年级《角的认识》

出示：钟表、剪刀、红领巾图

引导学生观察实物图，先在图上找到角，然后摒弃实物的物理属性，依托实物构建角的样子，初步感知角不仅仅有一个点，还有两条直直的线。

例2：二年级《认识长方形》

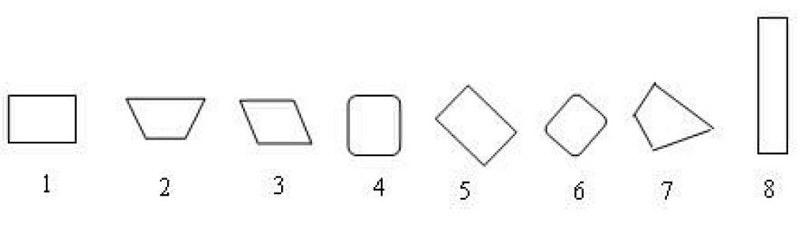
小学数学教材中，图形与几何知识的学习是螺旋上升的，基于二年级的学生已有一定的活动经验及思维经验，因此，〈认识长方形》教学可出示一些四边形：

观察并分类，在观察的基础上追问学生：1号、5号、8号这三个图形有的瘦，有的胖，有的斜，可你们都认为它们是长方形，这是为什么？立足于观察，引发学生初步感知长方形的模样，抛出问题，顺势而导，为后续从边和角两个元素研究长方形的特征作铺垫。这是学生初步感知几何图形的开始，对发展学生的形象思维，建立学生的空间观念很有帮助。

二、在操作中建立表象，抽象图形特征

操作是学生学习图形与几何的重要手段，通过操作能让学生亲身经历、体验图形知识的建构过程，建立图形的表象，在学生的认知里突显几何图形的大体轮廓和主要特征。因此，应让学生多动手操作，多方感官參与活动过程，抽象出图形的特征，借以发展空间观念，培养核心素养。

例1：五年级《长方体的认识》

小学生一年级就已经初步认识长方体，教师根据学生已有的认知经验，为学生提供搭建长方体的联结点和数目众多的小棒，让学生在小组合作中自行选择合适的小棒，动手搭一搭。

在展示交流搭好的长方体时，从点、线、面三个维度整体认识长方体的特征：①长方体共有6个面，相对的两个面完全相等。②两个面相交的那条线段叫做棱，有3组棱，其中水平方向上的棱分别叫做长方体的长和宽，竖直方向上的棱叫做长方体的高，长、宽、高分别有4条，共12条棱。③三条棱相交的点叫长方体的顶点，长方体共有8个顶点。通过动手搭一搭，在搭的过程中建立长方体的表象，掌握长方体的特征，发展学生动手操作能力，培养学生的空间观念。

例2：二年级《图形的运动——感知轴对称现象》

让学生“三剪”识对称。操作活动一：自由剪。让学生在自由状态下剪出一个爱心。学生动手剪的真实情况是：随手剪出的不对称的爱心和对折剪出的爱心，强调：先对折，再剪，左右两边才会一样。操作活动二：对折剪。出示衣服图，对折后再剪，呈现分成两半的衣服和一件完整的衣服。强调：在对折线上画一个记号，并在记号的对边画出衣服一半的轮廓，沿着轮廓剪。操作活动三：创造剪。教师给出对称图形，让学生找出图形的共同特征，感知轴对称现象。通过学生三次动手剪的操作活动，积累了认识轴对称现象的活动经验，为学生空间观念的发展做基础性积淀。

拉弗德认为：思维不是某些仅仅发生在大脑中的东西，它是由物质和想象的成分构成。课堂中教师总会担心一些静静坐在教室里的学生有没有在思考，这时不妨创设一系列活动，让学生动手操作，通过显性的“做”来体现学生隐性的“想”。

三、在想象中转换，沟通各方联系

空间想象是指对客观事物的空间形式进行观察、分析、抽象思维和创新的能力。在想象中自然转换，既可以沟通形与物之间的联系，也可以沟通形与形之间的联系，它对于提高学生的空间观念，培养数学核心素养意义重大。

1.想象可以是形与物之间的可逆性转换

如看到红领巾、三角尺会想到三角形，看到黑板、数学书会想到长方形；看到正方体会想到魔方、骰子，看到圆柱会想到水杯、茶叶罐……形与物的转换在我们的身边悄悄的进行着，只是我们从不曾用数学的眼光、数学的思维、数学的语言去留心它。

2.想象可以是形与形之间的可逆性转换

如认识了锐角三角形、直角三角形、钝角三角形后，出示点子图（如下图），想象：从图中选择三个点做顶点，用三条线段围成的三角形会是哪一类三角形？在这个想象的过程中，学生通过个性化的思考自我选择，再次在大脑中勾勒三类三角形，加深对三角形特征的认识，沟通三类三角形之间的联系与区别（至少有两个锐角，突出的一个角是直角那就是直角三角形，如果另一个角是钝角，那就是钝角三角形）。

爱因斯坦认为：想象力比知识更重要。通过想象可以毫不刻意地完成形与物之间、形与形之间的自然转换，丰富和发展学生的空间想象能力，培养学生推理能力和辩证思维，既发展了空间观念，又落实了数学核心素养。

四、在描述中厘清，表达图形的运动

语言是思维的外壳。语言描述可以是文字语言，也可以用符号语言，或者是二者的结合。描述能使学生对于图形的认知由感性的、直观的层面向理性的、抽象的层面提升。数学活动很多时候并不仅仅依靠直观的去感知，尤其是对于高年级的学生来说，更多的学习要把语言描述与表象形成紧密相联，进而转化成抽象的数学评议和简缩精炼的数学思维。

如学习图形的旋转时，先利用钟面，明确旋转的三要素之方向和角度，再出示点子图，提出问题：把线段AB按顺时针的方向旋转90度后画在方格图上。

1.汇报交流时，首先呈现三种方法，引发学生质疑：为什么同样是顺时针旋转90度，得到的图形会不一样？你看得懂吗？

2.让学生用数学的语言描述线段旋转的过程：方法一：线段AB绕A点顺时针旋转90度。方法二：线段AB绕B点顺时针旋转90度。方法三：线段AB绕中心点顺时针旋转90度。

3.引导学生整体体会旋转的含义，掌握旋转的三要素“中心、方向、角度”。在观察、比较的过程中，明确旋转后图形的形状、大小、旋转中心位置不变等特征。在用数学的语言（旋转三要素）正确表述图形旋转的过程中，既可以“你说要求我来画”，也可以“我画出旋转图形你来描述”，这两种逆向的问题方式，培养了学生的语言表达能力，发展了学生的空间想象能力，深化了学生的空间观念。

在核心素养背景下，教师要切实组织好课堂教学活动，为学生留足探索的时间与空间。这样的数学教学活动才能很好地提高学生的空间想象能力，发展空间观念，数学核心素养才能真正扎根于数学课堂。

[本文系福建省教育科学“十三五”规划课题《核心素养背景下数学思维养成的教学研究》（立项批准号FJJKXB17-309）的阶段性研究成果]

参考文献：

[1]中华人民共和国教育部 .义务教育数学新课程标准（ 2011年版） [M].北京：北京师范大学出版社 ，2012.

[2]马春霞.小学生数学空间观念的培养[J].新课程，2013，（06）.

[3]田凤娟.浅谈小学数学空间与图形教学[J].成才之路，2008，（17）.