基于ANSYS Workbench的水电站坝后浅埋管响应曲面优化分析
2018-07-20赵廷红马鹏强徐娜娜
赵廷红,马鹏强,徐娜娜
(兰州理工大学能源与动力工程学院,甘肃兰州730050)
近年来,随着水电站整体规模的日益增大,其引水建筑物压力管道的结构尺寸也变得越来越大。压力管道的具体尺寸通常在简化与假定的基础上采用经验公式、类比设计的方法确定,而且利用此类方法进行详细且较为精准地强度分析比较困难,故实际工程中有可能出现压力管道强度盈余过大,从而造成工程材料的浪费或者压力管道强度不足[1- 3]。压力管道的有限元优化设计在力学模型的建立上非常近似,在数学解法上完全严格,这样会大大提高结构的设计质量,且能在保证压力管道强度足够的前提下有效地降低压力管道的工程造价,具有显著的经济效益及社会效益。
本文以弹性力学、有限元基本原理、结构优化基本原理为理论基础,采用ANSYS Workbench大型有限元仿真软件进行结构应力分析与优化设计,对李家峡水电站坝后浅埋管结构[4- 5]分别进行了参数化三维实体建模、单元网格划分、结构应力与应变分析、状态变量与目标函数的设置以及优化参数的计算与评估,最终得到结构优化结果。
1 工程概况
李家峡水电站位于青海省尖扎县和化隆县交界处,地处黄河干流李家峡河谷中段,上距黄河源1 796 km,下距黄河入海口3 669 km,是黄河上游水电站梯级开发中的第3级大型水电站。坝型为混凝土重力坝,坝高165 m。电站安装5台混流式水轮发电机组(一期4台,二期1台),单机容量40万kW,总装机200万kW,平均年发电量59亿kW·h。压力管道采用“一机一管”的布设方式,由上平段、斜坡段、下弯段、下平段组成。钢管直径8.0 m,钢衬厚18~40 mm,外包混凝土厚1.5~2.0 m。钢管承受最大内水压力为1.520 MPa。
2 参数化三维建模
浅埋管直管段内径D=8.0 m,外包钢筋混凝土厚2.0 m,混凝土配置4圈钢筋(里圈、外圈各2层),间距20 cm。图1为管道在三维实体单元模型基础上利用多区域有限元网格划分法,将模型转化成的三维有限元单元模型,总共包含29 977个节点,12 784个单元。
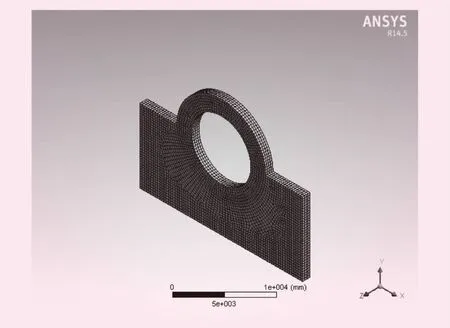
图1 管道三维有限元单元模型
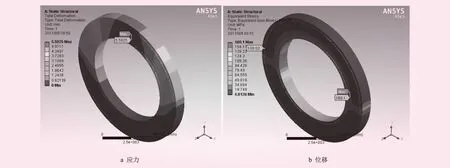
图2 管道有限元结构分析结果
3 有限元结构分析
在浅埋管下半圆外壁面处施加固定约束,在浅埋管管壁内施加大小为1.520 MPa、方向为垂直管壁向外的均布荷载,利用ANSYS Workbench中的DS模块对浅埋管进行有限元结构分析[7- 8],结果如图2所示。由图2可知,浅埋管最大位移出现在管道顶部,最大位移为5.592 5 mm;钢衬最大应力位于管道半腰处,为169.1 MPa,钢筋最大应力为109.02 MPa,而所选材料的屈服强度为320 MPa,均远大于结构的最大应力值。故为避免浅埋管强度、刚度盈余过大而造成材料浪费,需对其进行优化设计。
4 结构优化设计与分析
坝后浅埋管优化设计的目的是最大化地发挥钢材作用以达到节省钢材用量[9]。结构优化的主要内容为确定外包混凝土的最佳厚度、管道的最佳经济直径、钢衬的最佳厚度及环筋的最佳配筋率。按照目前的施工规范,外包混凝土厚度大概为管道直径的15%~30%,故只对管道直径、钢衬厚度及环筋折算厚度进行优化[10- 12]。
4.1 确定管道的最佳经济直径
为了输送满足水电站规定发电量所需的压力管道流量,需要确定相应的压力管道直径。当压力管道直径较小时,管内流速随之变大,相应的水头损失也变大,电能损失也随之增大;反之,当压力管道直径较大时,管道造价也随之增高,但损耗的电能却减少。因此确定合理的管道经济直径是很有必要的[13]。本文使用锅炉公式来确定管道经济直径D,即
D=2φ×(1-0.15)[σ] ×t/γH
(1)
式中,φ为焊缝系数,取φ=0.95;σ为钢管管壁钢材屈服应力;[σ]为钢材的容许屈服应力,[σ]=0.55σ;t为钢管管壁最大厚度;γ为水的重度,γ=9.8×103N/m3;H为管道最大内水压力,其中考虑钢材的容许应力降低15%。
本文算例李家峡水电站的H=152.0 m钢管管壁钢材屈服点,σ=330.00 N/mm2,t=40 mm。由式(1)可得,D=7.97 m。为保证一定的工程安全系数,拟定该工程的管道内径为D=8.0 m。
4.2 结构优化数学模型的建立
结构优化数学模型的建立包括设计变量、状态变量、目标函数的构建[14- 15]。
4.2.1 设计变量
结构优化设计中,设计变量为待确定的一些参数,这些参数反映了结构的形状大小、性能优劣等。在ANSYS Workbench结构优化设计中所设定的设计变量不能多于60个,各变量之间可以用数学表达式进行表示,简称参数耦合。设计变量通常用x1,…,xn表示,并构成一个向量[16],即
X=[x1,x2,…,xn]T
(2)
本文的设计变量为钢管厚度t和环筋折算厚度d,即X=[t,d]T,其中
d=(A×N)/l
(3)
式中,A为环筋折算面积,m2;N为直管段环筋数目;l为直管段环筋长度,m。
4.2.2 状态变量
状态变量是在结构优化设计用来限制结构状态的变量[17]。状态变量反映了结构关于设计规范、施工构造、工作强度等各方面的要求,使结构能够正常且有效地工作[14]。
本文的状态变量为:①每一层钢筋的环向应力σθ不得大于其容许应力[σθ];②压力管道钢衬厚度必须能保持外压稳定,即设计外压值P应小于临界外压值Pcr(d);③考虑制造技术、搬运过程、现场安装等外界因素,要求钢衬厚度t应大于钢衬的最小厚度δmin。
4.2.3 目标函数
目标函数是结构优化设计的最终目标,必须是设计变量的函数,代表结构设计的某个最重要的特征或指标[18- 19]。一般把目标函数表示为V。目标函数的类型有很多,通常有3种,分别为结构质量(质量最轻)、结构体积(体积最小)、结构造价(造价最低)。
本文的目标函数要求钢材总耗量最小,即钢材总体积V最小。取单位长度的压力管道进行分析,故只要求t和d最小,则目标函数表达式为
V=(t+d)×1,V→min
(4)
4.3 ANSYS Workbench优化计算
应用Workbench Design Exploration优化模块对结构进行优化分析,得到压力管道在最大内水压强1.520 MPa情况下所对应的优化成果,分别见图3~5。其中,图3为ANSYS Workbench给出的三种优化候选点,依据实际情况可以选取其中一种作为最终优化设计点;图4为响应曲面分析结果,图5为灵敏度分析结果,两者可以综合反映出设计变量里的哪个变量对优化结果的影响最大,因此可用于最终优化设计点的挑选。
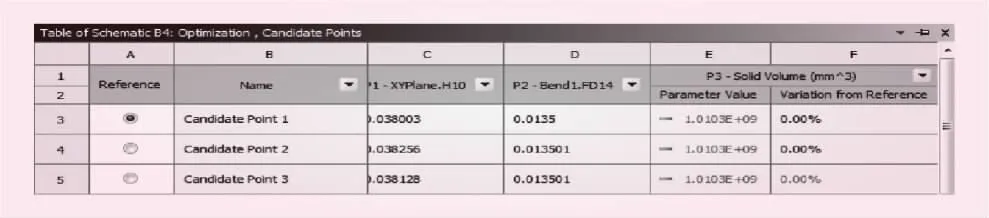
图3 参数优化候选点
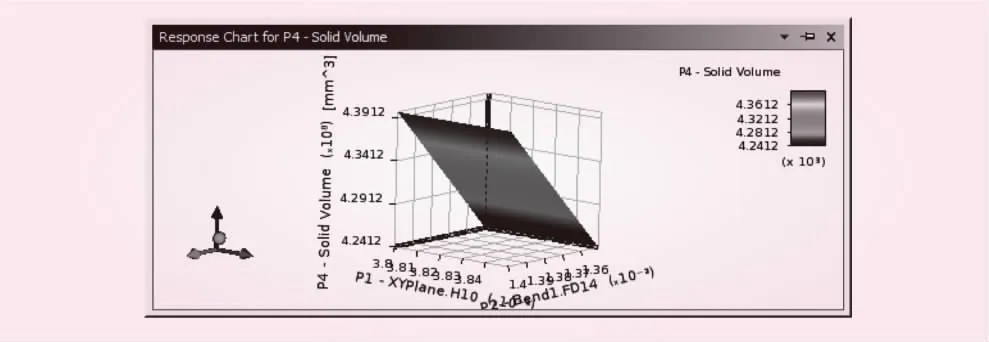
图4 响应曲面分析
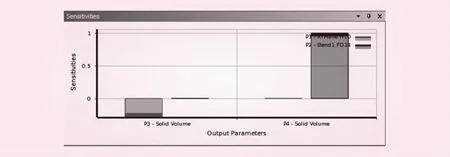
图5 灵敏度分析
最优设计序列选择3种优化方案里钢衬厚度较小的一种,即方案1,见表1。

表1 最优设计序列
4.4 管道优化前后对比
对优化后的管道施加与原模型相等的荷载再次进行结构分析,结果如图6所示,得到了最大应变值和最大应力值,与其原方案进行对比,结果见表2。优化后的管道与原来的相比较,最大变形量减少了0.28 mm,最大应力减少了7.69 MPa,单位长度的管道钢衬和钢筋总体积减少了0.062 m3,由此可知,优化后管道的耗钢量得到了一定的减少,且其结构性能也得到了一定程度的改善。
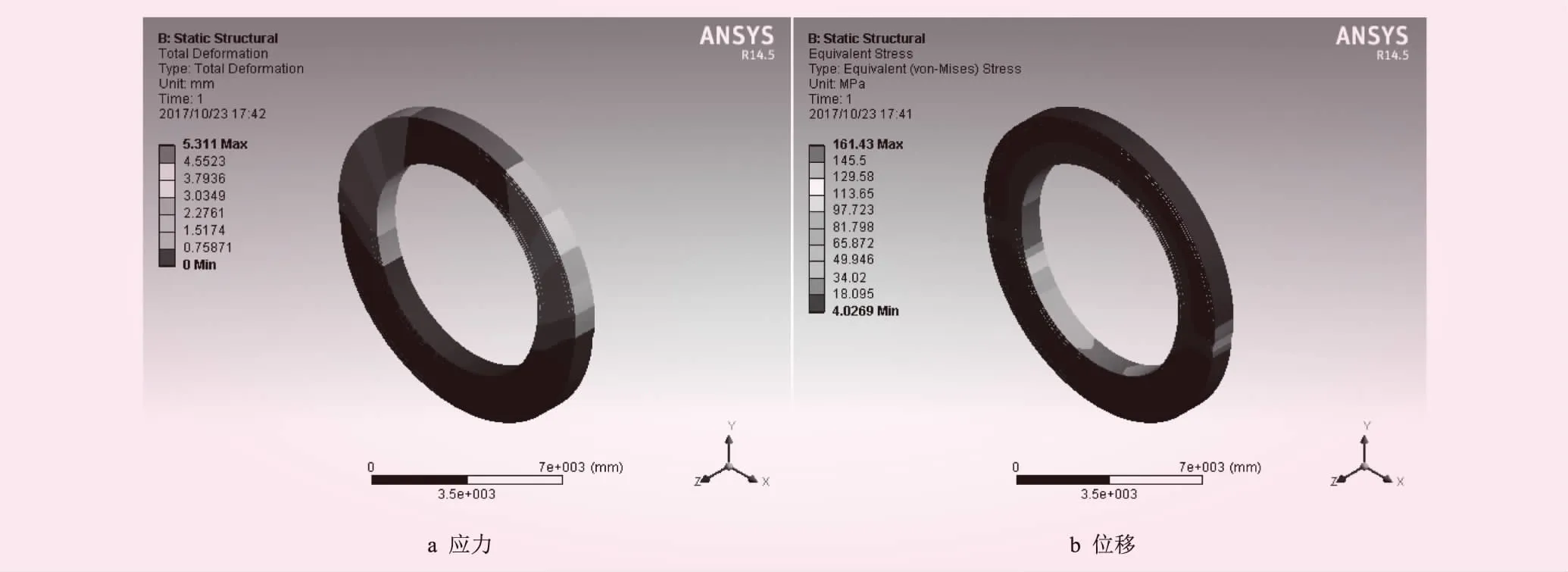
图6 优化后管道有限元结构分析结果

表2 优化方案与原方案特性比较
5 讨 论
将设计内水压强分为5个级别,分别为0.3、0.6、0.9、1.2、1.5 MPa,逐级施压,分别进行如上的优化计算,得到了在不同内水压下的最优钢衬厚度和最优钢筋折算厚度[20],变化规律见图7。
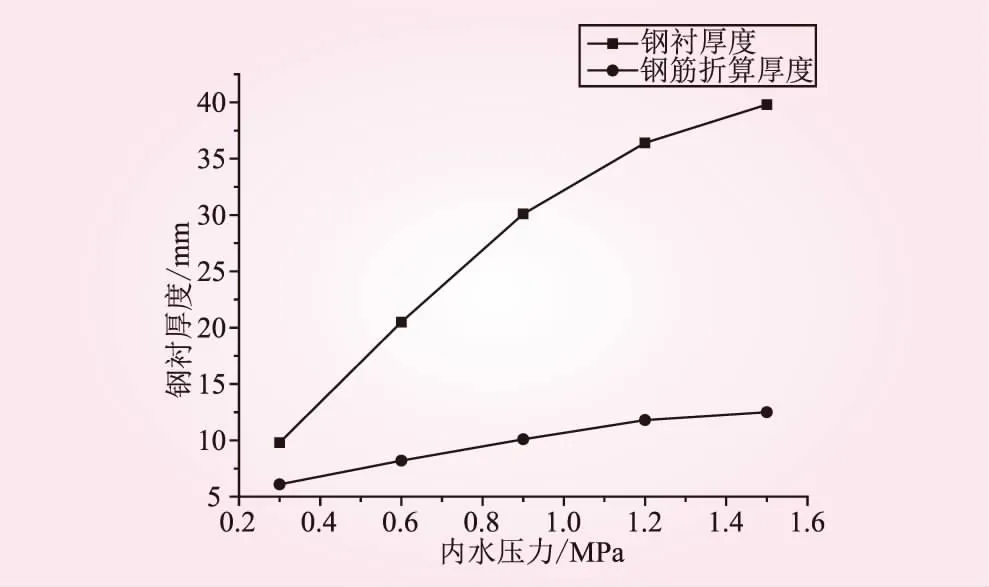
图7 不同内水压强下的钢衬厚度和钢筋折算厚度的变化规律
由图7可知,在满足状态变量的前提下,内水压力对钢衬厚度的影响比其对钢筋折算厚度的影响大,因此应给予钢衬强度、刚度以及稳定性足够多的重视。
6 结 论
根据给定的条件,利用ANSYS Workbench有限元优化设计对钢衬钢筋混凝土压力管道进行了结构优化,对比该工程的实际情况,得出如下结论:
(1)对压力管道用ANSYS Workbench进行优化分析,其优化结果能够正确反应具体工程的实际情况,确保压力管道的安全,使用响应曲面优化方法,可以使该工程在保证压力管道强度足够的情况下,节省钢材6.14%,可为同类压力管道的设计提供借鉴。
(2)在满足状态变量的前提下,内水压力对钢衬厚度的影响比其对钢筋折算厚度的影响大,应该对加强钢衬自身强度、刚度以及稳定性给予更多的重视。
(3)对于坝面浅埋管这种结构,由于其腰部会产生应力集中而导致其腰部应力急剧增大,应及时给予相关措施消除这种危害。
