不同改进的ARIMA模型在水文时间序列预测中的应用

杜 懿，麻荣永

(1.广西大学土木建筑工程学院，广西南宁530004;2.广西大学工程防灾与结构安全教育部重点实验室，广西南宁530004;3.广西大学广西防灾减灾与工程安全重点实验室，广西南宁530004)

0 引 言

ARIMA模型全称为自回归差分滑动平均模型(Autoregressive Integrated Moving Average Model)，是由Box和Jenkins于20世纪70年代初提出的一种时间序列预测方法[1- 2]。该模型具有较强的物理基础，由于结构简单、理论完备，在时间序列的预测中得到广泛应用。

近年来，随着全球气候变暖以及区域下垫面的剧烈变化，相当一部分水文时间序列表现出了高度的非线性特点。然而，传统ARIMA模型结构单一，不具备自适应学习能力，也难以挖掘出序列的原始信息，在应用中精度逐渐无法满足要求。对此，相关学者也进行了大量改进研究，但研究的重点往往集中在如何与其他预测模型(如灰色理论、神经网络、支持向量机等)进行加权组合，并通过优化算法(如遗传算法、粒子群算法、蚁群算法等)来确定最佳分配权重，进而提高模型预测精度；但并未涉及模型本身。基于此，笔者在具有高效线性预测能力的传统ARIMA模型基础上，结合新兴的非线性预测方法，对模型本身进行改进，以期获得更高精度。

1 模型介绍

1.1 ARIMA模型

模型的建模原理文献[3- 4]已有详细介绍，在此不再赘述。该模型具有3个参数，分别是自回归阶数(p)、差分次数(d)以及滑动平均阶数(q)，通常记作ARIMA(p，d，q)，表达式为

Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+
εt-(θ1εt-1+θ2εt-2+…+θqεt-q)

(1)

式中，Xt为研究的时间序列数据；φ1，φ2，…，φp为自回归系数；p为自回归阶数；θ1，θ2，…，θq为滑动平均系数；q为滑动平均阶数；εt为白噪声序列。

建模步骤主要包括数据预处理、模式识别、参数识别和模型检验四个部分，具体操作参见文献[5- 6]。

1.2 EMD-ARIMA模型

经验模态分解(Empirical Mode Decomposition)方法是由Huang等[7]人于1998年提出的一种信号分析方法。该法是对一个复杂的序列进行平稳化处理，将一系列具有不同层次的波动从原始序列中提取出来，得到若干个具有不同尺度的IMF分量[8- 9]。

对时间序列进行EMD分解，将所得的各项分别建立最合适的ARIMA(p，d，q)模型，再将各项的模拟结果进行累加求得最终的预测值。

1.3 WA-ARIMA模型

小波分析在时域和频域上同时具有良好的局部化特征，在处理非平稳时间序列中体现出很大的优越性[10]。小波分解时采用的小波种类很重要，目前常用的有Haar正交小波、Daubechies正交小波、样条小波、双正交小波等。本文选用db4小波，分解水平取4。

对时间序列进行小波分解，将所得的各项分别建立最合适的ARIMA(p，d，q)模型，再将各项的模拟结果进行累加求得最终的预测值。

1.4 BP-ANN-ARIMA模型

该模型是利用ARIMA模型来描述原始时间序列的线性关系，而用神经网络来拟合时间序列的非线性规律[11]。具体建模思路如下：

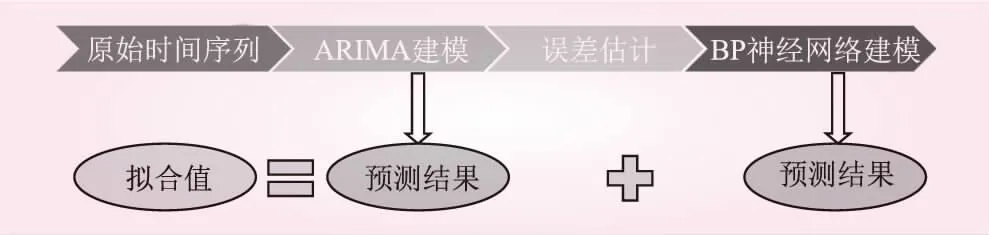
图1 BP-ANN-ARIMA模型建模过程

2 实例应用

本文选用南宁市1961年～2015共55年降水量资料进行预测研究，所用数据均来源自于广西壮族自治区统计局提供的《广西统计年鉴》及《广西水资源公报》。

2.1 ARIMA建模

借助SPSS 20.0统计分析软件对南宁市年降水量序列建立ARIMA(p，d，q)模型。先对整体序列进行自相关检验(见图2)。显然，原始序列即为平稳序列，无需进行差分处理，故差分次数d=0。为确定最佳自回归阶数p和滑动平均阶数q，分别初定不同取值进行比较，最终确定选用精度最高的ARIMA(1，0，1)模型。

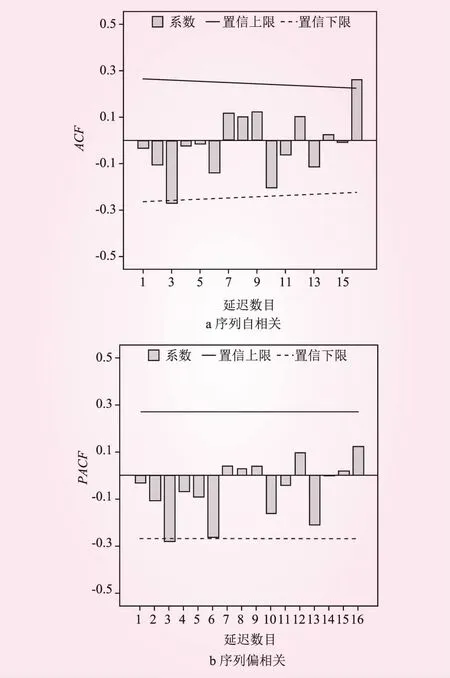
图2 南宁市年降水量序列的平稳性检验

2.2 EMD-ARIMA和WA-ARIMA建模

利用MATLAB 7.0编程软件对南宁市年降水量序列分别进行经验模态分解和db4小波分解，结果见图3、图4。

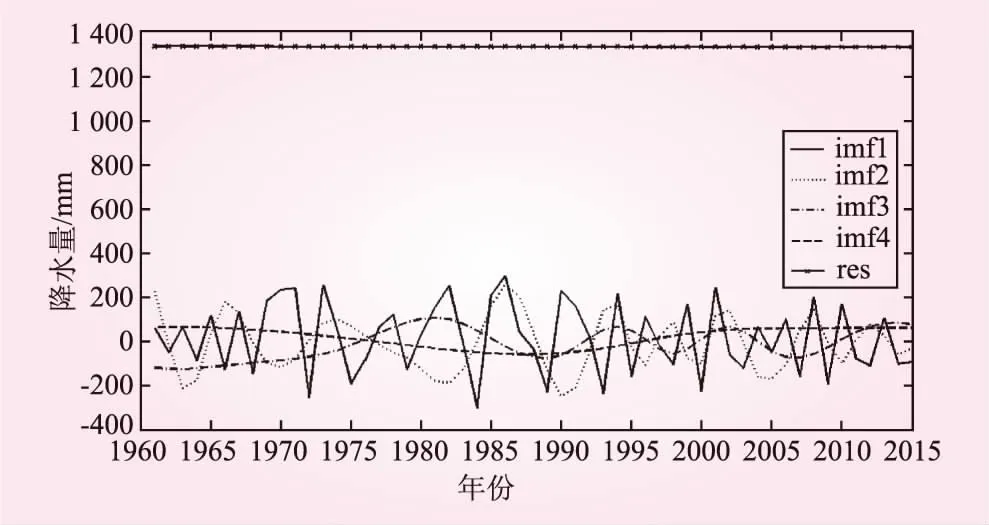
图3 南宁市年降水量的EMD分解结果

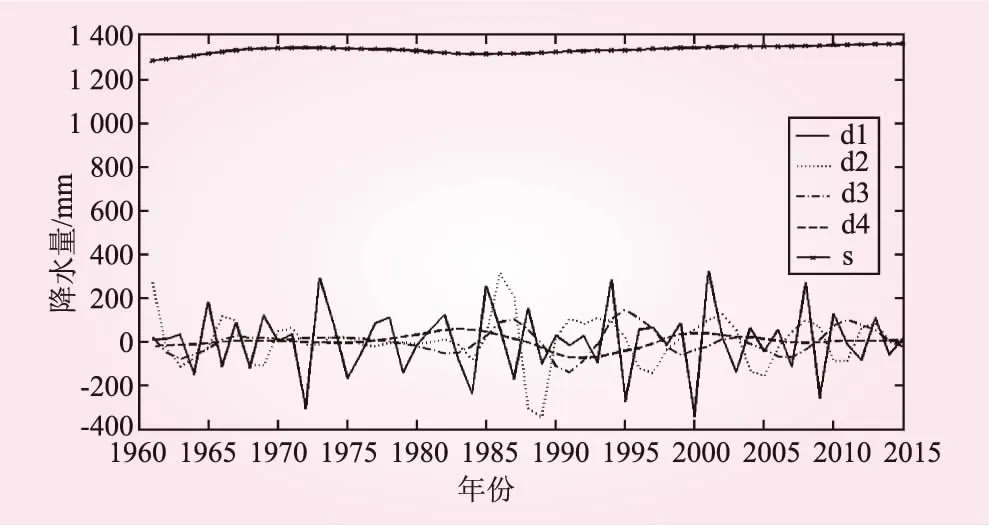
图4 南宁市年降水量的db3小波分解结果

由图3、4可以看出，两种分解方法结果类似，均存在1个低频成分(res项、s项)和4个高频成分(imf项、d项)，其中低频成分显示了时间序列的整体变化趋势。观察图3和图4，res项基本为一水平直线，而s项呈现出微弱的波动上升趋势，相比更能反映实际情况。

将两种分解模式下的各子项分别进行ARIMA建模，再将各子项的预测结果进行累加，得到最终的拟合值。在本例中由于s项、d4项、imf4项及res项为非平稳序列(经自相关、偏相关检验)，需要进行差分处理。分析得出，s项最适应ARIMA(1，2，1)模型，d4项、imf4项及res项适合ARIMA(1，1，1)模型，其余各项适应于ARIMA(1，0，1)模型。

2.3 BP-ANN-ARIMA建模

在BP-ANN-ARIMA模型的建模过程中，先利用ARIMA(1，0，1)模型对原始降水序列进行预测，经与实际值比较得到拟合残差。再以拟合残差为基础，建立经L-M算法优化的BP神经网络预测模型，模型设置2个历史节点，学习率取用0.075。最后将神经网络的预测结果与ARIMA(1，0，1)模型的预测结果叠加得出最终的拟合值(见图5)。

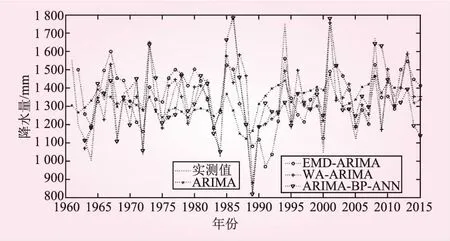
图5 各模型拟合过程比较

计算得，4种拟合模型的平均相对误差分别为11.2%、10.1%、6.8%、5.1%。其中BP-ANN-ARIMA模型表现最佳，拟合误差最小，说明了BP神经网络具有强大的非线性映射能力，十分适用于非平稳时间序列的预测。小波分解较经验模态分解效果要好，WA-ARIMA模型的拟合误差小于EMD-ARIMA模型，造成差别的原因在于对趋势项的提取，db4小波分解出的趋势项为波动缓幅上升趋势，更符合实际情况，而EMD分解没有体现出来。

3 结 论

以上模型在本次预测研究中均有较好表现，都达到了《水文情报预报规范》的规定。由于ARIMA是一种严格的线性预测方法，而绝大多数水文序列属于线性与非线性的综合，因而应用起来往往精度不高。为克服这一缺点，必须将其与非线性预测方法结合，这样既保留了模型本身的线性预测能力又弥补了其在非线性预测方面的不足。

本文将ARIMA模型分别与db4小波、EMD方法以及BP神经网络相结合，建立了3种不同的改进模型。实例表明，3种模型的预测精度均有不同程度的提高，尤其是结合了BP神经网络的ARIMA模型，平均相对误差仅为5.1%，这是基于神经网络强大的容错性与自适应性。