胶层热传递对挠性摆式微加速度计温度滞环的影响*

李 凯,罗 怡,2*,王晓东,2,孙屹博(.大连理工大学辽宁省微纳米技术及系统工程重点实验室,辽宁 大连 6024;2.大连理工大学精密与特种加工教育部重点实验室,辽宁 大连 6024)

20世纪40年代,德国研制了世界第1只摆式陀螺加速度计[1],应用于军用火箭V-2上,极大地提高了火箭的命中率。随着导航精度的不断提高,对加速度计的精度和稳定性的要求也不断提高。其中挠性微加速度计作为一种典型的光机电产品,近年来广泛应用于航天航空航海的惯性导航领域,针对其性能的提升,刘小院等针对挠性梁装配误差进行了研究[2]。严斌、刘云峰等研究谐振式加速度计非线性振动优化时发现谐振梁振动引起的非线性效应明显影响了系统的工作性能[3]。张宇飞、屈建龙等对石英挠性加速度计进行了温度补偿建模分析,结果表明补偿后的加速度计测量稳定性精度可提高5.55倍[4]。张习文研究了由摆片变形引起的零偏的温度稳定性,针对摆组件的胶粘接工艺提出了改进方法[5]。李玺,范锦彪,王燕等提出了微小型Hopkinson杆的动态校准系统,采用微小尺寸精密校准杆,并对传感器安装结构进行了改进,使得高安装谐振频率的高g值压阻加速度计进行动态校准得到的幅频特性曲线较为理想[6]。王猛,肖鹏,徐林鹏等针对硅微加速度计中微小差分电容检测提出了一种基于调制解调方法的闭环检测电路,并结合硅微加速度计的参数和电路设计参数,对加速度计系统进行仿真,仿真结果显示系统稳定,刻度系数为0.9 V/gn左右,带宽700 Hz左右[7]。Levy等人针对梁振动加速度计在温度变化环境下的补偿进行了研究[8]。Alauev等人基于补偿电路提出了高精度的温度补偿算法,可以用来改进加速度计的标度因素的稳定性[9]。Barulina等人建立了加速度计的综合模型,该模型包括热传导模型,动态漂移模型和微机械挠性梁模型等,获得了热应力和漂移等的定性和定量的参数[10]。

综上所述,国内外研究人员对加速度计性能稳定性提高做出了很多研究工作,但是对温度传递的研究较少。由于加速度计的工作环境温度在-45 ℃～80 ℃之间,而且零件之间连接方式多为胶粘接,因此当环境温度发生改变时,热量会通过壳体及空气传递到加速度计内部,使得加速度计内部空气场温度发生改变,进而影响加速度计各零件变形,胶的导热系数较于其他材料至少相差2个数量级,且胶层材料为环氧树脂,具有蠕变效应[11]。因此加速度计在环境温度发生改变时,挡光板位置会出现偏移,在升温过程和降温过程同一温度处偏值不等,出现温度滞环现象,影响加速度计性能稳定性。

挠性微加速度计存在装配零件多,零件加工精度和装配精度对加速度计性能耦合影响复杂的问题,通过实验的方法难以厘清不同零件间的胶层和胶层误差对加速度计性能的影响规律。因此本文通过数值仿真的方法对加速度计热传递及胶的蠕变效应共同作用对温度滞环的影响开展研究。

1 研究方法

1.1 加速度计三维模型特点

挠性微加速度计由底座、陶瓷块、挠性梁、三角架、挡光板等零件组成,其位置分布如图1所示。下壳体与陶瓷块1、陶瓷块1与挠性梁、挠性梁与陶瓷块2以及陶瓷块2与三角架等之间连接均为胶粘接,因此有4层胶,对称分布,即有8块胶。

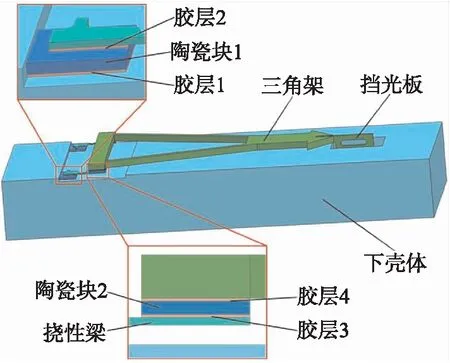
图1 加速度计胶层位置示意图

1.2 加速度计仿真模型建立

1.2.1 加速度计二维网格绘制

由图1可知,微加速度计具有零件多、胶层分布广泛、局部尺寸小等特点,因此在考虑空气作为热量传导介质的前提下,绘制其二维网格图作为研究模型,如图2所示。利用ICEM CFD绘制加速度计二维结构化网格图,将4层胶从下至上、从左至右分别命名为胶层1、胶层2、胶层3以及胶层4。

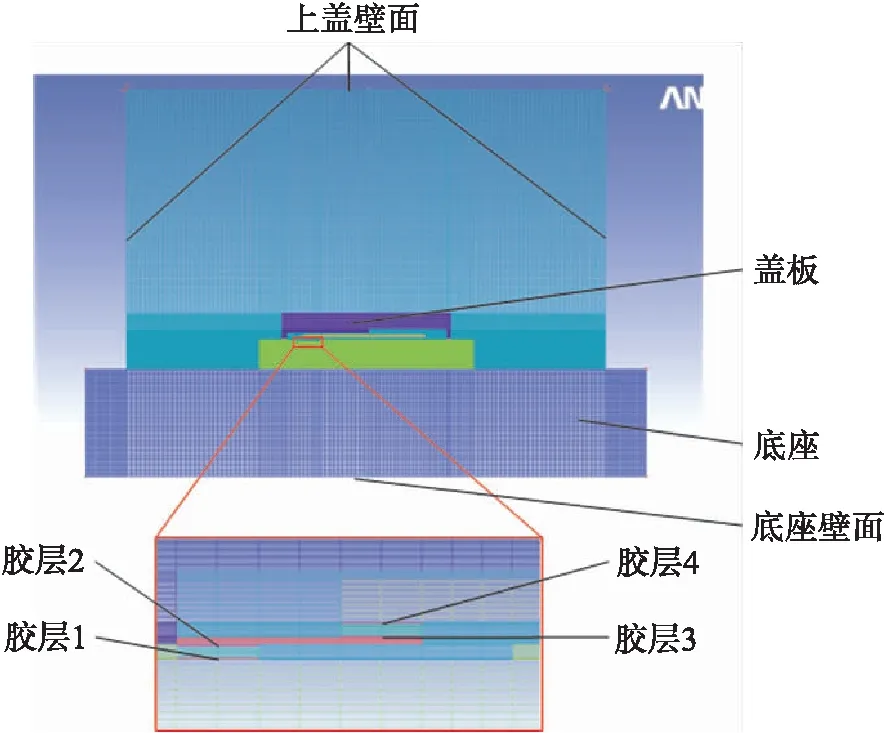
图2 加速度计二维网格图

1.2.2 热传递仿真模型及粘弹性仿真模型

将ICEM CFD绘制所得的加速度计二维网格图导入至Fluent中进行热传递仿真计算。各元件相应材料参数如表1所示。忽略热量由温箱壁面传递至底座及上盖这一过程,在仿真模型中将上盖壁面及底座壁面视作温箱壁面,在壁面处设置温度变化参数。又因为加速度计处于密闭环境中,其内部空气不与外界空气流通,仅与上盖及底座进行热量传递,因此在Fluent中打开能量方程,将空气视作传导热量的介质,仅做无规则对流。

在ABAQUS中建立加速度计粘弹性仿真模型如图3所示,网格绘制均采用六面体网格,其工作原理为粘弹性模型同时包含弹性(储存模量)和粘性(损耗模量),其静态表现为蠕变和应力松弛,动态表现为响应滞后[12]。ABAQUS则采用了更为复杂的粘弹性模型,通过试验曲线转化为Prony级数拟合粘弹性曲线[13],对于蠕变数据采用Burger模型:

(1)

对于松弛数据采用广义Maxwell模型[14]:

σ(t)=ε0E0+ε0∑Eie-t/τi

(2)

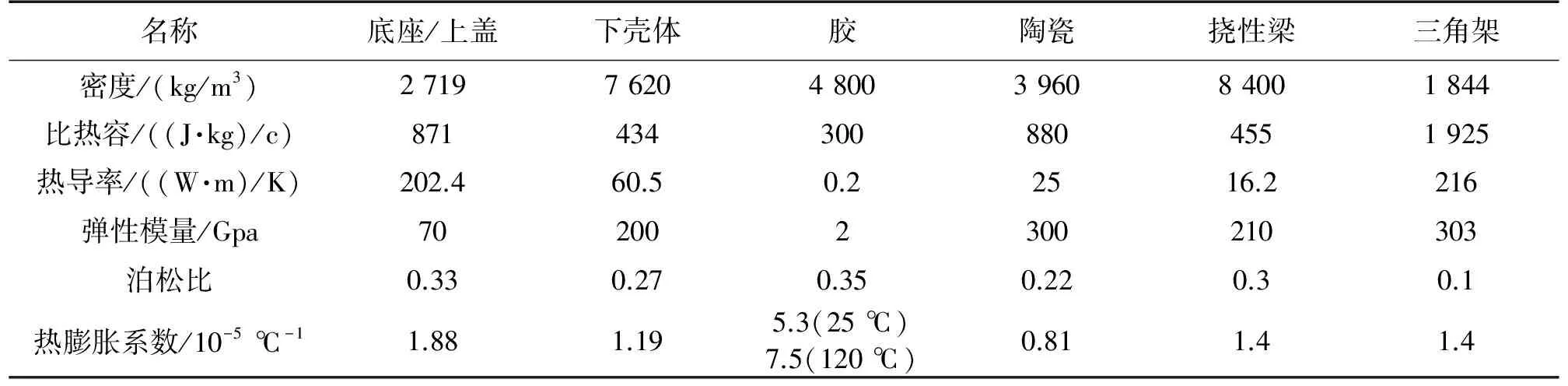
表1 各零部件材料参数

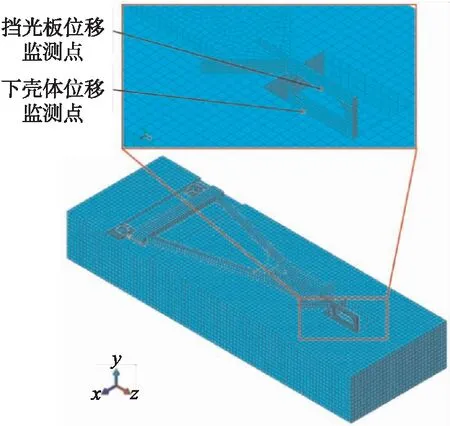
图3 加速度计粘弹性仿真模型网格图

由于加速度计所受温度循环载荷周期很长,属于准静态载荷,应属于静态粘弹性范畴,因此应用ABAQUS中的时域粘弹性模型进行仿真分析。实验测得胶层材料的蠕变柔量曲线,并输入至ABAQUS中,进行材料评估即可得到拟合的蠕变曲线。考虑热传递影响因素,将热传递仿真计算所得胶层处温度变化曲线加载至ABAQUS温度场中,由此建立加速度计的粘弹性仿真模型。

2 仿真结果与分析

2.1 Fluent热传递仿真分析

根据试验数据设置壁面温度变化参数为-45 ℃缓速升至80 ℃,升温速率0.6 ℃/min。在各胶层中心处设置温度监测点,用于提取胶层温度随时间变化曲线。设置400 min仿真计算,得出结果如图4所示。

由图4可看出胶层1和胶层2中心点处温度变化曲线变化规律基本一致,胶层3和胶层4中心点温度变化曲线规律基本一致,且均滞后于温箱壁面温度变化曲线,另外在升降温初始阶段和稳定阶段,胶层处温度变化速率明显缓慢。由于胶层面积很小,因此提取胶层中心点处温度变化曲线可视作胶层所处温度场温度变化曲线。将热传递仿真分析所得的胶层3中心点处升降温历程结果合并,设置两个温度循环历程应用于ABAQUS热应力仿真模型温度场作为温度载荷,如图5所示。

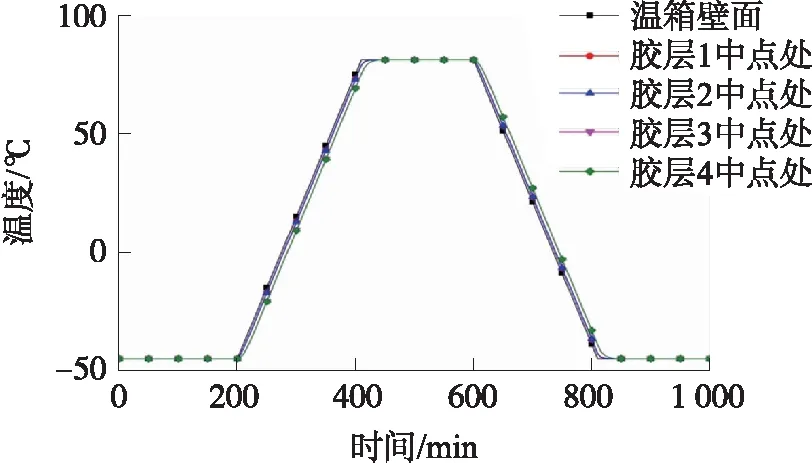
图4 -45 ℃～80 ℃升降温过程仿真结果

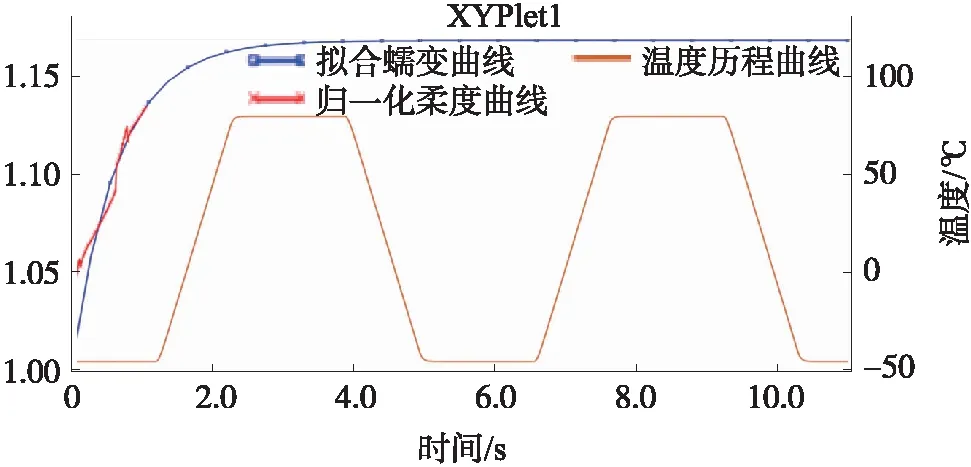
图5 温度循环历程对应胶层材料的拟合蠕变曲线

2.2 ABAQUS热应力仿真分析

2.2.1 无胶层误差理想模型仿真结果

微加速度计设计的理想胶层厚度均为10 μm,没有厚度、倾斜、溢出等误差。计算此状态的温度滞环值作为有误差因素影响的温度滞环值的参照,此状态下的仿真模型命名为“Ideal-model”。在粘弹性模型中进行热力学仿真分析,如图5所示,拟合后的蠕变曲线与温度载荷时间对应关系,在分析步中设置两次温度循环,第1周期温度循环处于蠕变初始阶段,第2周期处于蠕变稳定阶段,第3周期及以后周期滞环值与第2周期几乎一致,本文不作考虑。

从仿真结果中提取挡光板上侧中点和下壳体Y方向对应点在温度历程中的位移,如图6所示,带点实线为挡光板监测点位移曲线,实线为温度循环历程曲线,带点虚线为下壳体监测点位移曲线。由于下壳体材料为金属,因此对于温度的变化反应较快,因此下壳体监测点位移曲线变化规律与温度循环历程曲线基本一致,而挡光板监测点与下壳体之间有四层胶层,因此其监测点位移变化曲线受到胶层蠕变效应的影响变化规律与温度循环历程曲线相似度较低,图中有一个突变点,这是因为蠕变突变引起的。

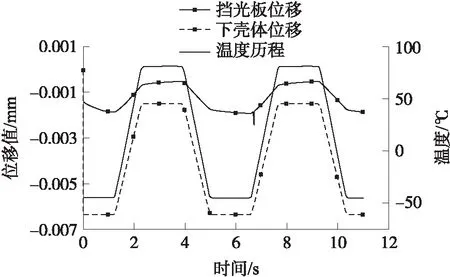
图6 加速度计节点位移及温度曲线图

提取以上二检测点位移及对应温度,定义同一温度点处升温过程挡光板和下壳体之间的位移差值与降温过程二者位移差值之差的绝对值为滞环最大值,简称滞环值,如表2所示,根据结果可见第1周期滞环值明显大于第2周期,此二者将作为以下胶层有误差模型的参照。

表2 无误差模型两个周期下的滞环值

2.2.2 胶层厚度对滞环值的影响

在胶的涂覆过程中,由于其粘度影响,通常胶的厚度都小于10 μm。因此针对加速度计的胶层,厚度分别为9 μm,8 μm,7 μm以及6 μm进行仿真,与标准状态下的10 μm的结果进行对比,如图7所示,得出温度第1周期滞环值如图7(a)所示,温度第2周期滞环值如图7(b)所示。

由图7可知,胶层2厚度为6 μm时对加速度计滞环值影响很大,第2周期滞环值可达64.4 μg,第1周期滞环值可达125.4 μg;胶层1、3、4厚度误差对加速度计滞环值影响不大,第1周期滞环值在96 μg～106.4 μg之间,第2周期滞环值在50.6 μg～55.2 μg之间;任何一层胶层有厚度误差,第2周期滞环值必然增大。这是由于胶层自身粘弹性能抵消一部分因温度变化产生的蠕变应变,当胶层厚度低于一定值蠕变应变就会凸显。而不同胶层所处位置不同,胶层厚度误差对滞环值的影响差异明显。

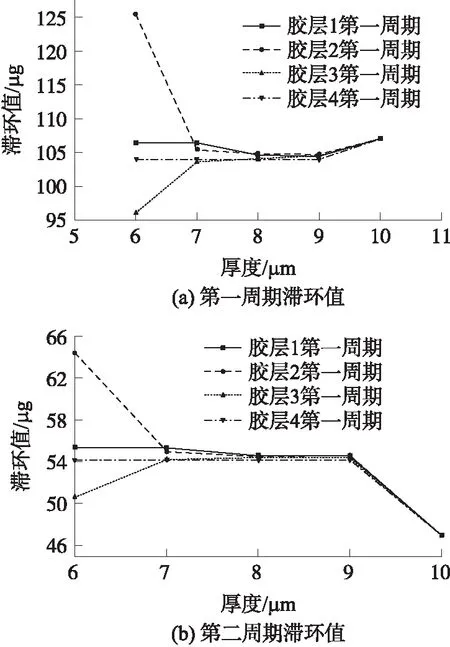
图7 胶层厚度误差模型滞环值曲线图

2.2.3 胶层溢出对滞环值的影响

针对加速度计四层胶层,分别设置4组胶层溢出误差,胶层溢出部分设置为等腰三角形,如图8所示,将其边长作为溢出误差量度。

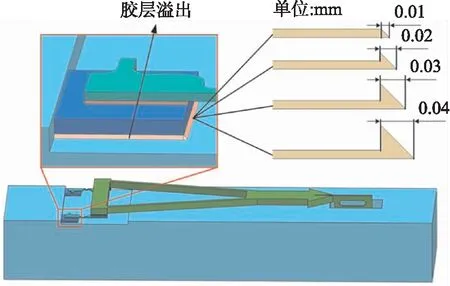
图8 胶层溢出误差示意图

4组溢出量分别为10 μm、20 μm、30 μm以及40 μm。具有胶层溢出误差的这16组模型前处理均与无胶层误差理想模型一致,对这16组有胶层溢出误差模型进行仿真计算,处理仿真结果与无胶层误差模型一致,得出温度第1周期滞环值如图9(a)所示,温度第2周期滞环值如图9(b)所示。

由图9可知,胶层3溢出量增加时,第1周期及第2周期滞环值均显著增大,最大可达260 μg和128.8 μg;胶层1、2、4溢出误差对加速度计滞环值影响较小,第1周期滞环值在97.6 μg～111.8 μg,第2周期滞环值在51.6 μg～58.2 μg;任意一层胶层有溢出误差,必然引起加速度计第2周期滞环值增大。

图9 胶层溢出误差模型滞环值曲线图

胶层溢出部分产生的蠕变应变会通过挠性梁、三角架等被放大,胶层3处于挠性梁后半部分,其溢出部分产生的蠕变应变较其他胶层放大较为明显。而溢出越大,在后续装配过程剥离的可能性越大,且有可能产生胶层缺陷,对加速度计整体性能和安全性产生不良影响,因此在胶层涂覆过程应严格控制胶层溢出量。

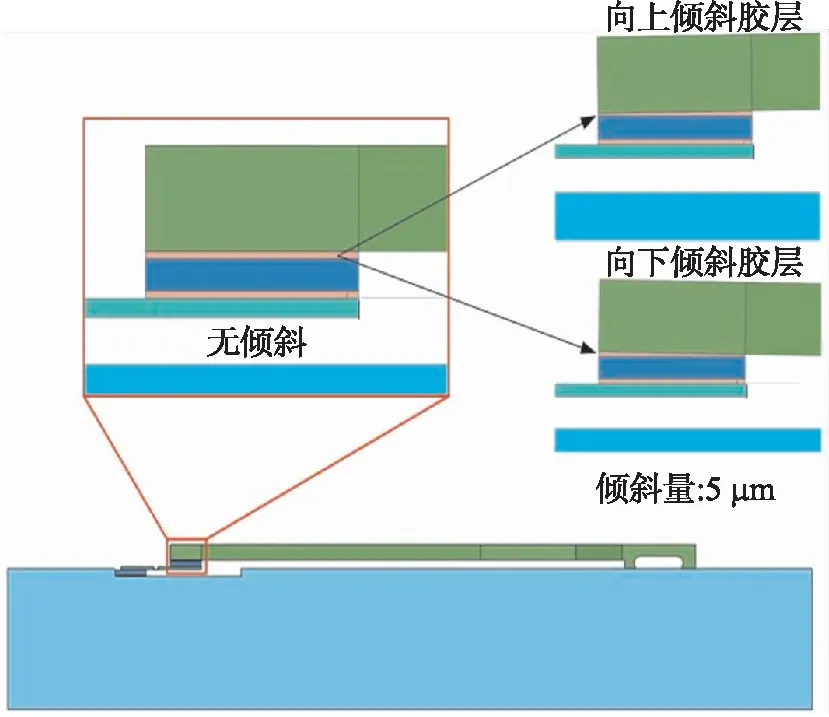
图10 胶层倾斜误差示意图

2.2.4 胶层倾斜对滞环值的影响

分别设置2组胶层倾斜误差,一组使得挡光板向下倾斜,一组使得挡光板向上倾斜。胶层的倾斜量均为5 μm,如图10所示,得出温度第1周期滞环值如图11(a)所示,温度第2周期滞环值如图11(b)所示。

由图11可知,若胶层倾斜误差导致挡光板向下,加速度计第1周期滞环值小于标准状态;若胶层倾斜误差导致挡光板向上,加速度计第1周期滞环值大于标准状态,最大可达120 μg;胶层倾斜误差均会引起第2周期滞环值变大,最大可达62.6 μg。胶层倾斜使得挠性梁和三角架水平方向倾斜,各胶层产生的蠕变应变得到进一步放大,使得滞环值变化明显。

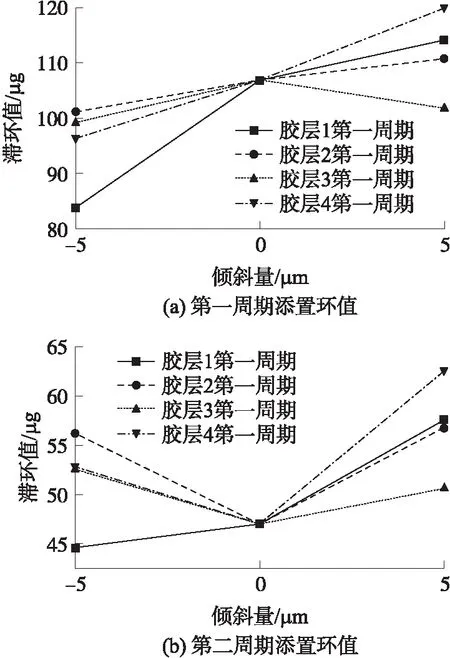
图11 胶层倾斜误差模型滞环值曲线图

3 结论

本文针对挠性微加速度计装配中的胶层,研究热传递和蠕变效应的共同作用对加速度计温度滞环的影响,着重考虑手工涂胶导致的胶层厚度、溢出和倾斜等误差因素。

仿真结果表明,胶层的第1周期滞环值和第2周期滞环值表现不同,明显高于第2周期,第2周期后就趋于一致,第1周期滞环值处于初始蠕变过程,呈现加速度计初期或久置后刚使用时的性能,第2周期滞环值处于稳态蠕变过程,呈现加速度计稳定运行时的性能。因此对于加速度计的精确滞环补偿可分步进行。

仿真结果显示,胶层2厚度为6 μm时,第2周期滞环值可达64.4 μg,第1周期滞环值可达125.4 μg;任意一层胶层的厚度误差均会引起第2周期滞环值变大;胶层的溢出误差对加速度计滞环值影响很大,胶层3的第1周期滞环值最大可达260 μg,第2周期最大可达128.8 μg;倾斜误差也会导致滞环值变化,其中胶层4的影响最大,向上倾斜误差使第1周期滞环值达120 μg,第2周期滞环值达62.6 μg。

本文通过对挠性微加速度计的胶层进行粘弹性仿真分析,得到以下对胶层涂覆工艺的建议:在装配过程中严格控制胶层2的涂覆厚度,避免低于6 μm;胶层3的涂覆应严格控制溢出量;胶层4的涂覆过程应严格控制其倾斜误差。