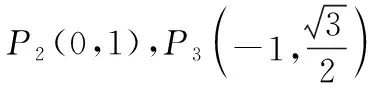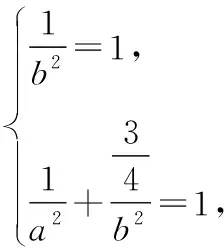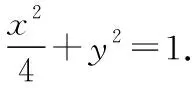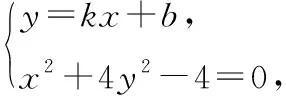从两道高考真题看“数学核心素养”的体现
2018-07-20湖南罗礼明
湖南 罗礼明
高中数学新课程标准修订版提出了数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等六大数学核心素养.数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的关键能力与思维品质,也是确保课程改革整体推进的核心.数学教学中,数学核心素养的落实的迫切性日趋引起重视,作为“指挥棒”的高考试题如何落实核心素养的考查?教育部教育考试院2017全国卷试题评价中总结到:“2017年高考数学试题以立德树人、服务高校人才选拔、导向中学教学为命题出发点,加强对理性思维的考查,渗透数学文化,突出创新应用能力与数学核心素养的考查,体现了数学的科学价值和理性价值,有利于高校选拔优秀人才,有利于引导中学数学教学,特别在数学课程和教学改革中提升学生的核心素养有积极的导向作用.”本文以2017全国卷Ⅰ数学理科两道试题为例摭谈其“数学核心素养”的体现.
案例1
一、题目再现
(2017·全国卷Ⅰ理·19)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:

9.9510.129.969.9610.019.929.9810.0410.269.9110.1310.029.2210.0410.059.95

附:若随机变量Z服从正态分布N(μ,σ2),
则P(μ-3σ 解析:(1)抽取的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.997 4,从而零件尺寸在(μ-3σ,μ+3σ)之外的概率为1-0.997 4=0.002 6,所以X~B(16,0.002 6),故P(X≥1)=1-P(X=0)=1-0.997 416≈0.040 8.X的数学期望E(X)=16×0.002 6=0.041 6. (2)(ⅰ)如果一天生产状态正常,一个零件尺寸在(μ-3σ,μ+3σ)之外的概率只有0.002 6,一天内抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有 0.040 8,发生的概率很小,因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的. 本题是概率统计的实际应用,数学味道正,生活气息浓,将知识、能力、思想、方法融为一体,解题关键在于读懂题意,联想所学知识,合理选择运算策略.本题主要考查了统计与概率中的两个重要的概率分布模型:二项分布和正态分布.综合考查数学抽象、逻辑推理、数学运算、数据处理、数学建模等数学核心素养的应用,要求对基本模型、基本原理和基本思想有深刻的理解. 1.会用数学的眼光观察现实世界,即接收外界输入的信息,并对信息进行数学抽象与直观想象.将现实生产中的产品抽样检测问题用合理的数学原理进行解释;“这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2)”用数学的知识来直观理解就是“正常状态下生产的零件的尺寸99.74%合格”,即正常状态下生产不合格零件是小概率事件,且X~B(16,0.002 6). 案例2 (1)求C的方程; (2)设直线l不经过P2点且与C相交于A,B两点,若直线P2A与直线P2B的斜率的和为-1,证明:l过定点. 解析:(1)根据椭圆对称性,必过P3,P4, (直观想象) 又P4横坐标为1,椭圆必不过P1,所以椭圆过P2,P3,P4三点. (逻辑推理) (数学抽象) (数学运算) (2)①当l的斜率不存在时,设l:x=m, 由题设知,m≠0,且|m|<2,A(m,yA),B(m,-yA), 解得m=2,此时l过椭圆右顶点,不存在两个交点,不满足题意. (数学抽象) ②当l的斜率存在时,设l∶y=kx+b(b≠1), A(x1,y1),B(x2,y2), (直观想象) 整理得(1+4k2)x2+8kbx+4b2-4=0, (数学运算) 又kP1A+kP1B=-1,所以b=-2k-1, 此时Δ=-64k,存在k使得Δ>0成立. (逻辑推理) 所以直线l的方程为y=kx-2k-1,过定点(2,-1). (数学抽象) 本题主要考查椭圆的标准方程,直线与圆锥曲线的位置关系及数学运算、逻辑推理与数学抽象等核心素养,主要表现为考查运算的合理、敏捷性,将运算技能与思维能力有机结合,重点考查算法与算理.椭圆的对称性是椭圆的一个重要性质,判断点是否在椭圆上,可以通过这一方法进行判断;证明直线过定点的关键是设出直线方程,通过一定关系转化,找出两个参数之间的关系式,从而可以判断过定点情况.另外,在设直线方程之前,若题设中未告知,则一定要讨论直线斜率不存在和存在情况,接着通法联立方程组,求判别式、韦达定理,根据题设关系进行化简. 启示 在解答数学问题时,将新问题转化为旧问题、未知问题转化为已知问题、复杂问题转化为简单问题的过程中用到的基础知识、基本技能和基本思想只有在具体求解时才能发挥作用,经历解答的过程才能积累基本活动经验,而在问题解决中起决定性作用的却是六大核心素养.核心素养的三个方面,六个关键词既独立,又相互交融,形成一个有机整体.我们在日常教学中落实新理念,以核心素养为指向,帮助学生把一个个具体知识理解到位并能用于解决问题.二、规范解答
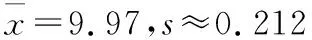
三、核心素养的分析与提炼
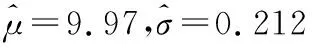
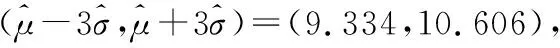
一、题目再现
二、规范解答与核心素养体现