一二三四五 天体搞清楚
2018-07-20湖北荣万军
湖北 荣万军 向 锋 郭 爱
随着中国航天事业的蓬勃发展,高考也更加偏向于以最新的航天科技成果为背景进行命题,突显课程性质和学科精神,响应国家提出的培养核心素养号召。万有引力定律与航天是高考的超级热点,几乎算得上是必考点。从考纲要求来看,万有引力定律及其应用和环绕速度属于Ⅱ级要求,归类为重点知识,而第二宇宙速度、第三宇宙速度及经典时空观、相对论时空观属于Ⅰ级要求,仅作了解。另外万有引力定律涉及概念和模型较多,公式繁多且灵活多变,学生易错易混,是高中物理的一个关卡。本文试图通过一句话“一二三四五,天体搞清楚”来介绍重难点,供师生参考。
一、理解一条定律
万有引力定律主要考查其公式的适用条件和灵活运用。
1.公式的适用条件
【例1】一个质量均匀分布的球体,半径为2r,在其内部挖去一个半径为r的球形空穴,其表面与球面相切,如图1所示。已知挖去小球的质量为m,在球心和空穴中心连线上,距球心d=6r处有一个质量为m2的质点,则剩余部分对m2的万有引力为 。

图1
【点评】此题是万有引力定律的经典题目,涉及定律本身、合力和分力、球形体积公式等知识。


【感悟】公式的适用条件是求解质点之间或者等效成质点的匀质球间的引力;引力半径6r和5r的使用最易出错。
【变式训练】某地区的地下发现天然气资源,如图2所示,在水平地面P点的正下方有一球形空腔区域内储藏有天然气。假设该地区岩石均匀分布且密度为ρ,天然气的密度远小于ρ,可忽略不计。如果没有该空腔,地球表面正常的重力加速度大小为g;由于空腔的存在,现测得P点处的重力加速度大小为kg(k<1)。已知引力常量为G,球形空腔的球心深度为d,则此球形空腔的体积是
( )
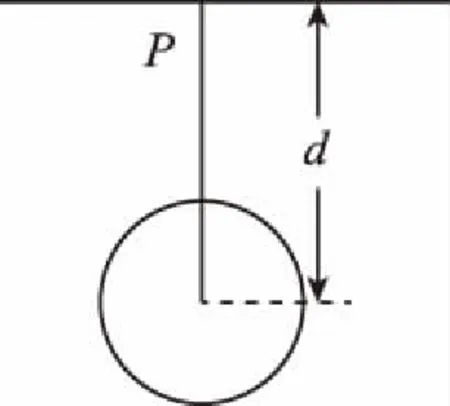
图2


【点评】此题考查的是万有引力定律的应用。

【答案】D
【感悟】忽略自转时重力等于万有引力(g值的应用),体会割补法的应用。
2.公式的灵活运用
【例2】理论上已经证明:质量分布均匀的球壳对壳内物体的万有引力为零。假设地球是一半径为R、质量分布均匀的实心球体,O为球心,以O为原点建立坐标轴Ox,如图3所示。一个质量一定的小物体(假设它能够在地球内部移动)在x轴上各位置受到的引力大小用F表示,则下图所示的四个F随x的变化关系图正确的是
( )

图4

图3
【点评】此题是由2012年的全国卷改编的一道信息题,考查万有引力定律公式的灵活运用。
【答案】A
【感悟】抓住信息:质量分布均匀的球壳对壳内物体的万有引力为零,将球体分成两部分(球体与球壳),类似例1和变式训练。
二、掌握两种模型
两种模型是绕地模型和随地模型。绕地模型就是卫星绕地球做匀速圆周运动。随地模型就是地表物体随地球自转,通常考查两种情况:忽略自转(简单)和考虑自转(较难)。
【例3】如图5所示,地球赤道上的山丘e,近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动。设e、p、q的圆周运动速率分别为v1、v2、v3,向心加速度分别为a1、a2、a3,则正确的是
( )

图5
【点评】此题考查两种模型的区别与联系。

【答案】D
【感悟】地表物体要通过同步卫星才可与其他卫星进行参量的比较。
三、学会三种方法
天体运动问题计算量大,要适当掌握估算的技巧,而公式繁多则要善用比例法,对于空间位置要会找几何关系。
1.估算法
【例4】“嫦娥一号”是我国首次发射的探月卫星,它在距月球表面高度为200 km的圆形轨道上运行,运行周期为127 min。已知引力常量G=6.67×10-11N·m2/kg2,月球的半径为1.74×103km,利用以上数据估算月球的质量约为
( )
A.8.1×1010kg B.7.4×1013kg
C.5.4×1019kg D.7.4×1022kg
【点评】天体运动经常考查学生的估算能力。

【答案】D

2.比例法

( )


【点评】比例法在天体运动的计算中运用频率较高。




【答案】B
3.几何法
【例6】宇宙飞船以周期T绕地球做圆周运动时,由于地球遮挡阳光,会经历“日全食”过程,如图6所示。已知地球的半径为R,地球质量为M,引力常量为G,地球自转周期为T0。太阳光可看作平行光,宇航员在A点测出地球的张角为α,则下面正确的是
( )

图6
【点评】由几何关系寻找物理量间的关系是高考考查学生运用数学方法解决物理问题的常见方式。
【答案】D

图7
四、熟悉四个重点
1.计算天体质量及密度
【例7】如图8所示,“天宫二号”在距离地面393 km的近圆轨道运行。已知万有引力常量G=6.67×10-11N·m2/kg2,地球质量M=6.0×1024kg,地球半径R=6.4×103km。由以上数据可估算
( )

图8
A.“天宫二号”质量
B.“天宫二号”运行速度
C.“天宫二号”受到的向心力
D. 地球对“天宫二号”的引力
【点评】此题容易产生思维定式且易将中心天体和环绕天体的质量弄混淆。

【答案】B
【感悟】“引进外资”法(即绕地模型)只能求中心天体的质量,无法求出环绕天体的质量。
2.人造卫星和宇宙速度
【例8】我国自主研制的“嫦娥三号”,携带“玉兔”月球车已于2013年12月2日1时30分在西昌卫星发射中心发射升空,落月点有一个富有诗意的名字——“广寒宫”。若已知月球质量为m月,半径为R,引力常量为G,以下说法正确的是
( )




【点评】考查第一宇宙速度和重力加速度的求解方法。

【答案】C
【感悟】月球上的第一宇宙速度和加速度可以类比地球上的方法求解,实现方法的迁移,而弄清参量变化是关键。
3.多星问题
【例9】太空中存在一些离其他恒星很远的、由三颗星体组成的三星系统,可忽略其他星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统——三颗星体始终在一条直线上;另一种是三角形三星系统——三颗星体位于等边三角形的三个顶点上。已知某直线三星系统A的每颗星体的质量均为m,相邻两颗星中心间的距离都为R;某三角形三星系统B的每颗星体的质量恰好也均为m,且三星系统A外侧的两颗星体做匀速圆周运动的周期和三星系统B每颗星体做匀速圆周运动的周期相等。引力常量为G,则正确的是
( )




【点评】本题考查三星系统的两种形式。
【解析】在第一种形式下如图9所示 :三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行。

图9

【答案】BCD
【感悟】轨道半径和引力半径是易错点,向心力和几何关系是难点。
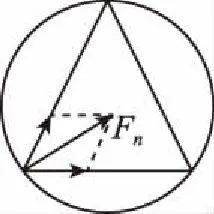
图10
4.变轨问题
【例10】2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图11所示,关于航天飞机的运动,下列正确的是
( )
A.在轨道Ⅱ上经过A的速度小于经过B的速度
B.在轨道Ⅱ上经过A的动能小于在轨道Ⅰ上经过A的动能
C.在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期
D.在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度

图11
【点评】本题是典型的卫星变轨问题,综合考查了圆周运动的动力学问题和开普勒第二、三定律。

【答案】ABC
【感悟】进高轨要加速,掉低轨要减速;转移轨道是椭圆,要用开普勒三定律;有时还要辅助一个圆轨道进行比较。
【变式训练】如图12为“嫦娥三号”登月轨迹示意图。图中M点为环地球运动的近地点,N为环月球运动的近月点。a为环月运行的圆轨道,b为环月球运动的椭圆轨道,下列说法中正确的是
( )

图12
A.“嫦娥三号”在环地球轨道上的运行速度大于 11.2 km/s
B.“嫦娥三号”在M点进入地月转移轨道时应点火加速
C.设“嫦娥三号”在圆轨道a上经过N点时的加速度为a1,在椭圆轨道b上经过N点时的加速度为a2,则a1=a2
D.“嫦娥三号”在圆轨道a上的机械能小于在椭圆轨道b上的机械能
【点评】本题以“嫦娥三号”登月为背景,对比考查卫星的发射和回收。
【解析】11.2 km/s为第二宇宙速度,“嫦娥三号”在环地球轨道上的运行速度小于11.2 km/s,故A错误;从低轨道进入高轨道需点火加速,故B正确;“嫦娥三号”在a、b两轨道上N点,受月球引力相同,根据牛顿第二定律可知,加速度也相同,即a1=a2,故C错误;从轨道a进入轨道b需在N点加速,所以机械能增大,即轨道b上机械能大于轨道a上的机械能,故D正确。
【答案】BD
【感悟】三个宇宙速度的实质都是对圆周运动动力学的考查;机械能可以通过变轨时的加、减速进行比较,只受万有引力时机械能守恒。
五、化解五大难点
1.自转难点
【例11】设地球自转周期为T,质量为M,引力常量为G。假设地球可视为质量均匀分布的球体,半径为R。同一物体在南极和赤道水平面上静止时所受到的支持力之比为
( )

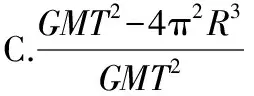
【点评】此题考查自转中的受力问题。

【答案】A
【感悟】地表物体随地球自转绕地轴做匀速圆周运动的特点:与地球自转具有相同的周期;支持力与重力等大反向;万有引力和支持力的合力提供物体做匀速圆周运动的向心力。另外谨防任何情况下万有引力都等于重力的定式思维。
2.重力加速度
【例12】物体在地球表面重16 N,地面上重力加速度为10 m/s2。它在以5 m/s2的加速度加速上升的火箭中的视重为9 N,则此火箭离地球表面的距离为地球半径的
( )
A.2倍 B.3倍
C.4倍 D.一半
【点评】此题考查牛顿运动定律和万有引力定律的应用。

【答案】B
【感悟】视重就是物体受到的支持力或者拉力,可以不等于重力;火箭加速上升时,重力变化是难点,而将视重当作重力是易错点。
3.追及相遇
【例13】某行星和地球绕太阳公转的轨道均可视为圆。每过N年,该行星会运行到日地连线的延长线上,如图13所示该行星与地球的公转半径比为
( )

图13


【点评】本题是典型的天体追及问题,综合考查了圆周运动和开普勒第三定律。

【答案】B
【感悟】追及问题必须找出各相关物理量间的关系,通常利用圆周运动“(角)位移关系”列方程,或者能直接将(角)位移关系转化成转动圈数关系,运算过程更简洁。相距“最近”或“最远”是突破口,相遇次数和绕行方向可造成多解。
4.信息题型
【例14】2011年 8月,“嫦娥二号”成功进入了绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家,如图14所示,该拉格朗日点位于太阳与地球连线的延长线上,一飞行器位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的
( )
A.线速度大于地球的线速度
B.向心加速度大于地球的向心加速度
C.向心力仅由太阳的引力提供
D.向心力仅由地球的引力提供

图14
【点评】飞行器与地球同步绕太阳做圆周运动是题干中的关键信息。
【解析】飞行器与地球同步绕太阳运动,角速度相等,根据v=ωr,知飞行器的线速度大于地球的线速度,故A正确;由a=ω2r知,飞行器的向心加速度大于地球的向心加速度,故B正确;飞行器的向心力由太阳和地球引力的合力提供,故CD错误。
【答案】AB
【感悟】新信息类题目需要对所给信息反复阅读,直到明白若飞行器只受地球引力或者只受太阳引力都不能与地球同步绕太阳做圆周运动,其向心力必须由太阳和地球引力的合力提供。
5.天体的能量变化

( )

图15


【点评】题目中给出了引力势能的表达式,考查天体的能量变化。
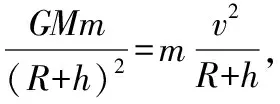
【答案】D

