速度关联类问题求解策略

山东 张启光 李瑞芳

运动物体间速度关联问题是有些高考命题的切入点，寻找速度关联关系是考生普遍感觉的难点。关联意味着双方服从某种共同条件的制约，即等量关系，而寻找等量关系应当从两个研究对象的共同之处着眼，这是解题关键。本文从同体关联和异体关联两大类进行该问题的分析。

一、同体关联

所谓“同体关联”问题，是指同一根绳(或杆)的两端连着两个物体，其速度各不相同，常常是已知一个物体的速度和有关角度，求另一个物体的速度。要顺利解决这类题型，需要搞清两个问题：

(1)分解谁的问题：哪个运动是合运动就分解哪个运动，物体实际经历的运动就是合运动。切记，可以分解的一定是实际速度，即实际速度是合速度。

(2)如何分解的问题：由于绳(或杆)不能伸缩，所以沿同一绳(或杆)上的速度分量大小相等，将合速度分解成一个沿绳(或杆)方向的速度和一个垂直于绳(或杆)方向的速度，即将合速度向沿绳方向作“投影”，根据两个端点的速度沿着绳(或杆)方向的分速度大小相等列式求解。

1．绳端关联

【例1】一辆车通过一根跨过定滑轮的绳PQ提升井中质量为m的物体，如图1所示，绳的P端拴在车后的挂钩上，Q端拴在物体上，设绳的总长不变，绳子质量、定滑轮的质量和尺寸、滑轮上的摩擦都忽略不计，开始时，车在A点，左右两侧绳都已绷紧并且是竖直的，左侧绳长为H，提升时，车加速向左运动，沿水平方向从A驶向B，设A到B的距离也为H，车过B点时的速度为vB，求在车由A移到B的过程中，绳Q端的拉力对物体做的功。

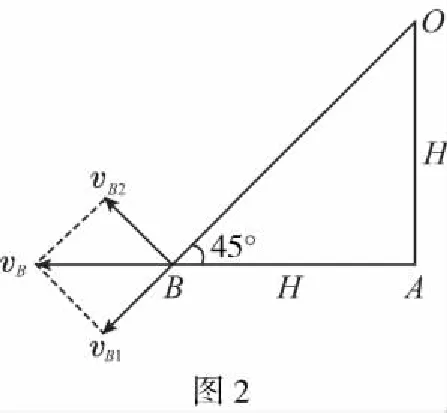
【点评】通过定滑轮的绳两端连接两个物体时，两端物体在沿绳方向上的分速度大小相等。

【例2】如图3所示，物体A置于水平面上，A前固定一滑轮B，高台上有一定滑轮D，一根轻绳一端固定在C点，再绕过B、D。BC段水平，当以速度v0拉绳子自由端时，A沿水平面前进，求：当跨过B的两段绳子夹角为α时A的运动速度v。

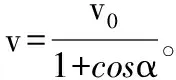
【点评】一个物体与几条绳相关联时，每条绳独立研究，物体的实际速度在每条绳上的分速度等于该方向收绳的速度；绳一端固定，另一端通过动滑轮拉物体时，另一端拉绳的速度是动滑轮两侧收绳速度之和。

2．杆端关联

【例3】如图4所示，均匀直杆上连着两个小球A、B，不计一切摩擦。当杆滑到如图位置时，B球水平速度为vB，杆与竖直方向夹角为α，求此时A球速度。

【解析】A球速度向下，B球速度向右，由于杆不能伸缩，所以两球沿杆方向的分速度相等，分别对小球A和B的速度沿着杆方向和垂直于杆方向进行分解有：vAcosα=vBsinα，解得vA=vBtanα。

【答案】vBtanα

【点评】通过杆两端连接两个物体时，把物体的实际速度沿杆和垂直杆方向进行分解，两端物体在沿杆方向上的分速度大小相等；另外有固定转动轴的杆端关联是有共同的角速度。

二、异体关联

所谓“异体关联”问题，是指两个物体没有连接在一起，仅通过接触等方式联系在一起，要顺利解决这类运动物体间的速度关联题型，关键是选取合适的连结点，即与两物体相联系的分运动，依据平行四边形定则分解速度，寻找速度关系列式求解。

1．异体接触带动关联

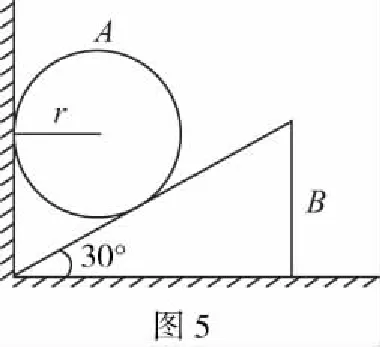
【例4】如图5所示，斜劈B的倾角为30°，劈尖顶着竖直墙壁静止于水平地面上，现将一个质量与斜劈质量相同、半径为r的球A放在墙面与斜劈之间，并从图示位置由静止释放，不计一切摩擦，求此后运动中斜劈的最大速度。

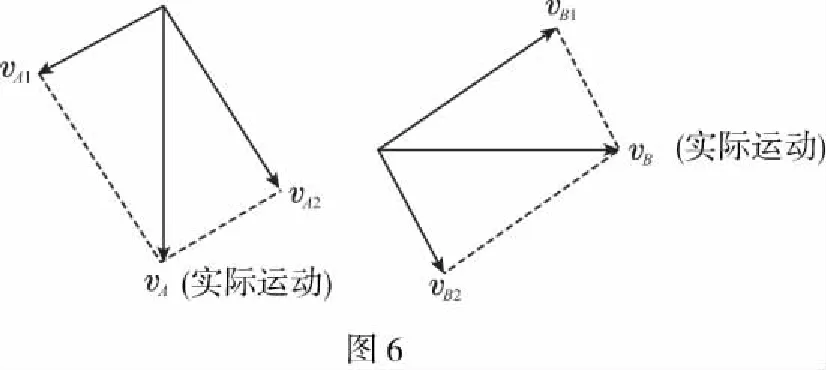
【点评】两个相互接触的物体，一个物体运动导致另一物体运动的这类速度关联问题，因为垂直接触面方向两物体相对静止，所以两物体实际速度在垂直接触面的方向上的分速度相等。

2．相对运动的线状物体交点速度

【例5】 如图7所示，A、B为半径相同的两个半圆环，以大小相同、方向相反的速度运动，A环向右，B环向左，则从两半圆环开始相交到最后分离的过程中，两环交点P的速度方向和大小变化为 ( )

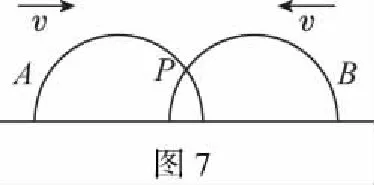
A．向上变小

B．向下变大

C．先向上再向下，先变小再变大

D．先向下再向上，先变大再变小

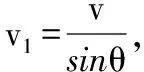
【答案】C

【点评】相对运动的线状物体交点是两者相对运动引起，所有交点的速度是两者分别运动引起交点移动速度的合速度，先分别假设相对运动的两个物体中的一个静止，求出另一物体运动时交点的速度，再把求得的这两个速度求矢量和就是交点的实际速度。

3．照射关联

【例6】如图9所示，S为一点光源，M为一平面镜，光屏与平面镜平行放置，SO是垂直照射在M上的光线，已知SO=L，若M以角速度ω绕O点逆时针匀速转动，则转过30°角时，光点S′在屏上移动的瞬时速度v为多大？

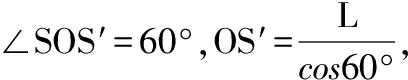
【答案】v=8ωL