三相四线电能表失压退补电量的误差研究

邢晓敏，孙 成，陈劲游，商国敬，朱敏珊

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.中山供电局，广东 中山 528400；3.大唐东北电力试验研究所有限公司，吉林 长春 130000)

随着电网规模的不断扩大，电能表数量不断增加，每年因电能表失压故障需要追补电量的问题日益突出.众所周知，电能表是发电厂上网电量、电网损耗和供给用户电量的计量设备，其准确可靠性与电力交易双方的合法利益密切相关[1～2].目前电能表失压退补电量所采用的方法主要有“更正系数法[2～3]”、“电量平衡法[4～5]”、“相邻表计电量法[6～8]”等等.这些方法都存在各自问题，而且主要依靠人工计算，误差大、费工费时.为此，本文采用一种新的计算方法——电压替代法，可以实时计算三相电能表失压退补电量.该方法不仅克服了传统方法需要假定三相负荷电流平衡的缺点，实现了失压退补电量的直接抄读，而且根据其样机在校表台上设置三相平衡电压的情况下，模拟三相电流各种不平衡状态进行了更正电量误差测试，且测试结果误差小于0.5%[9]，但实际的电网三相电压不一定是理想的平衡状态.根据“电压替代法”原理，电网三相电压不平衡必然会产生计算误差.为此，还需要从理论上定量分析在实际电网三相电压不平衡范围内，该方法的计算误差，确保电压替代法退补电量的精确度远优于传统人工计算退补电量的方法.

1 误差研究的理论依据

电能表失压时所计电量是电能表故障时实际计量的电量，也称故障电量.失压故障时故障电量大多数情况是比实际用电量(也称为正确电量)少，特殊情况也有可能会多，总之不能正确计量实际用电量，需要退补比实际用电量少计或多计的部分.失压时不能直接得知实际用电量，只能用其它的办法得到接近正确电量的更正电量.更正电量减故障电量，为正值，表示电能表少计了电量，用户应补交电量；为负值，表示电能表多计了电量，应退还用户的电量，统称为退补电量[10].各量之间的关系为：退补电量=更正电量-故障电量.其中，电能表失压时实际电量，即故障电量是已知量，要想退补电量准确，只需更正电量准确.所以，根据电量与功率之间的关系，可以进一步转化为求更正功率的误差.可表示为

(1)

式中：γ为更正功率误差；P为正确功率；P″为更正功率；ΔP为更正功率与正确功率差.

2 “电压替代法”计算更正功率误差

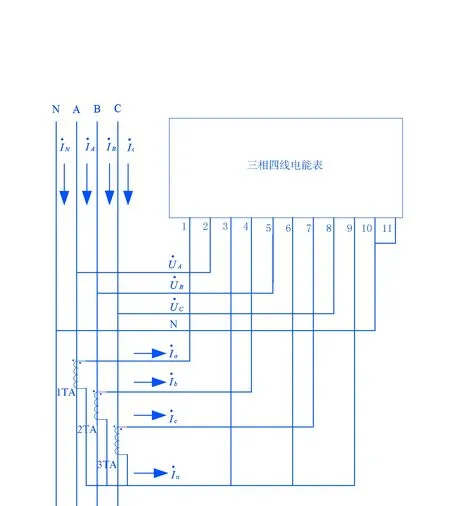
图1 三相四线电能计量装置接线图

图2 三相四线A相失压时电压电流矢量图

“电压替代法”是用非失压相电压幅值替代失压相电压幅值，用正常相电压与相应的电流的相位差计算出失压相的更正电压电流相位差，以此相位差代替失压相电压电流相位差，从而计算出更正功率.由于该方法不需假设三相负荷平衡，也不用考虑故障相二次侧残压的问题，而且电网的三相电压不对称度的变化范围远小于用电负荷变化范围、三相电流不对称度变化范围以及失压相残压的变化范围，所以电压替代法是目前误差小、投资少(只需在现有多功能表、负荷管理终端增加退补电量的计算模块)、可直抄读退补电量、运维管理简单的具有很好推广应用前景的新方法.

现以三相四线计量A相失压[5～7]为例分析其更正电量误差.三相四线计量原理接线图，如图1所示.

利用各相电压、电流表示的正确有功功率为

P=UAIacosφA+UBIbcosφB+UCIccosφC

，

(2)

其复数功率为

(3)

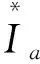
P″=UBIacos(120°-ψaB)+UBIbcosφB+UCIccosφC

，

(4)

当三相电压不对称时UA≠UB，φA≠120°-ψaB，则P″≠P，即更正功率不等于正确功率.为便于用对称分量法求取其差值，根据式(4)写出P″的复数功率为

(5)

更正功率的复数功率与正确功率的复数功率差为

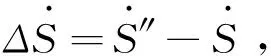
代入式(3)和式(5)得：

(6)

以A相作为基准相，利用“对称分量法[11～12]将式(6)等效变换为

(7)

式中：U1、U2、U0、I1、I2、I0分别为A相电压、电流的正序、负序和零序分量；下标1表示正序，下标2表示负序，下标0表示零序.

将式(7)展开并取其实部可得更正有功功率与正确有功功率差：

(8)

式中：φ21、φ01、φ22、φ02、φ20、φ00分别是各相序电压与电流的相位差，下标第1个数字代表电压的相序，下标第2个数字代表电流相序.

电力系统电压、电流不平衡是指三相电压、电流在幅值上不同或相位差不是120°，或兼而有之.不平衡的程度是用电压、电流负序基波分量或零序基波分量与正序基波分量的方均根值表示，称为电压、电流的负序不平衡度和零序不平衡度[13-17].将式(8)代入式(1)，分子、分母同除以U1I1得：

(9)

式中：εV2、εV0、εI2、εI0分别为电压负序不平衡度、电压零序不平衡度、电流负序不平衡度、电流零序不平衡度.

在实际电网中，εV2εI2和εV0εI0的积远小于1.按《电能质量 三相电压不平衡》规定，电网正常运行时负序电压不平衡度不超过2%.对零序电压不平衡度该标准虽没有做出具体规定，但规定电压必须满足《电能质量供电电压偏差》的要求，有关规程还规定，配电变压器零序电流不得超过低压绕组额定电流的25%，这时电压零序不平衡度约为5%[18].可见有：εV2为2%、εV0为5%、εI2为25%、εI0为25%，可得：

εV2εI2=0.02×0.25=0.005<<1 ，

εV0εI0=0.05×0.25=0.012 5<<1 .

由于式(9)中cosφ2和cosφ0同时为1或-1时对分母影响最大，如果同时为1，分母中与εV2εI2和εV0εI0积有关的二项和为0.0175，而实际电网正序功率因数cosφ1一般在0.8以上，上述二项和对分母的影响不超过0.02，所以分母中与εV2εI2和εV0εI0积有关的二项可忽略不计，又由于式中相位差太多，使得误差计算复杂，即分子中各正弦函数值可从-1到1之间变化，故按误差最大的原则，同时取值为1或-1，则式(8)可以简化为

(10)

可见式(10)无需知道各相序相位差，只需增加负序电压、零序电压、负序电流、零序电流或者是不平衡度的监测功能，正常时为监测电能质量(电压不平衡度)，故障时根据故障前监测数据计算退补电量误差范围.但是，式(10)分母cosφ1是正序功率因数，而通常可以得到的是三相功率因数，故需进一步分析讨论.

由于实际电网三相不平衡度有限，且实际电网的负序功率、零序功率之和远远小于正序功率，所以可以视cosφ≈cosφ1，将其代入式(10)得：

(11)

同理可以计算B相、C相单相失压或二相失压更正功率误差.由式(11)可知，电压负序、零序不平衡度对误差影响大，而且电流的负序、零序不平衡度对误差也有影响.当三相电压对称，即三相电压负序不平衡度和零序不平衡度都为0时，更正功率误差为0.由于更正电量等于更正功率乘以时间，则更正电量的误差也为0.这与定性分析一致.

3 误差变化曲线分析

下面分析实际运行的功率因数及三相电压、电流不平衡度在一定范围变化时更正电量误差变化情况.

由式(11)可知，功率因数越低误差越大.功率因数过低将增加电网损耗，对不同类型用户有0.9、0.85、0.80考核标准，低于考核标准的将加收电费.实际电网大多数情况功率因数大于0.85，现取功率因数最低考核标准cosφ=0.8，设A相和B相电流为I，C相电流为KII，KI是C相电流相对于其它项电流的变化系数，各相电流相位差为120°，A相电压为ΔU+U，B相和C相电压为U，各相电压相位差为120°，电能表A相失压，计算“电压替代法”更正功率误差变化情况.

根据上述条件利用“对称分量法”等效可得到电流负序、零序不平衡度为

(12)

式中：I1、I2、I0分别为正序电流、负序电流和零序电流.

电压负序、零序不平衡度为

φ≈φ1=30°

，

(13)

式中：U1、U2、U0分别为计算正序电压、负序电压和零序电压.

将式(12)、(13)代入式(11)得：

(14)

当三相最大相与其它二相电压差△U从-6 V到6 V，C相电流系数KI取不同值时，按式(14)计算的误差变化线图，如图3所示.由图3可知误差变化范围，电压差△U绝对值越大，误差越大，当KI为0时，即C相电流为0时，误差最大.KI从0.0、0.5、1.0、2.0到5.0时误差变化线斜率减小、也就说明误差越小，图中误差变化线用由深变浅表示.

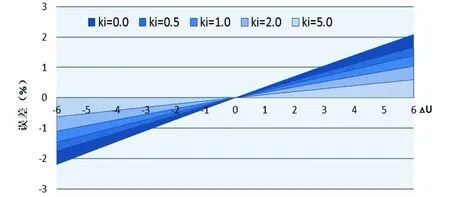
图3 误差变化线图

为更加严谨，排除不平衡度过大的特殊情况，本文采用正常时监测的正、负、零序电压、电流，并根据研制的样机电能表和负控等有计量功能的终端实现了该监测功能.不仅正常时能为监测电能质量(电压不平衡度)、降损节能、淘汰落后高能耗变压器、平衡三相用电负荷提供监测数据，而且故障时还可根据故障前电网三相电压、电流不平衡范围，利用误差计算公式(14)很容易计算退补电量误差范围.只要根据误差范围，就可以判断“电压替代法”是否适用.

4 按约束条件分析计算误差

通过上述分析，得出了“电压替代法”在三相电压、电流负序、零序不衡条件下更正电量误差公式(11).为了说明“电压替代法”在实际电网大多数情况下的误差，现选取三种不平衡条件计算A相失压更正电量的误差值.

相关标准或规程规定的最大不平衡约束条件为εV2≤2%、εV0≤5%、εI2≤25%、εI0≤25%并取cosφ=0.866，代入公式(11)得A相失压更正电量的误差值为7%，该误差是在相关标准或规程规定的约束条件同时最大时的误差，因而误差较大.由于电网规模的扩大，节能意识提高，特别是变压器制造水平的提升，电网电压不平衡度水平有了很大提高，同时出现上述极限平衡情况较少，此处只是说明不平衡条件较大时误差范围.笔者设计的样机在现场安装时配电变压器低压侧负序电压未超过1 V、零序电压未超过2 V.按此条件分别计算出电压负序不平衡度为0.455%、零序电压不平衡度为0.91%，如其他条件不变，代入公式(11)得A相失压更正电量的误差值为1.36%，可见安装到现场的样机其更正电量的计算误差较小.

上述两种情况都是比较特殊时的约束条件，很难代表大多数情况.为此，本文对某实际电网13 479台配电变压器日负荷率最大时三相电压数据进行了统计计算，结果有95%的变压器各相电压最大差值不大于6 V.为便于计算，设A相电压比其它二相大6 V，即226 V，B相和C相电压为220 V，各相电压相位差为120°，电能表A相失压，A相和B相电流为I，功率因数为cosφ=0.866，即φ=30°，C相电流为0，分别计算“电压替代法”更正功率误差和传统“更正系数法”计算更正功率误差[7].将计算结果进行比较.

(1)将上述条件代入公式(11)得A相失压更正电量的误差值为

(2)利用传统“更正系数法[1-4]计算更正功与实际用电功率的误差为

表1 两种方法误差计算结果

这是取C相电流为0电流不平衡度较大的情况.如果取C相电流分别取0.4I、0.727I，I为A、B相电流，可计算其电流负序和零序不平衡度0.4I时为25%，0.727I时为10%，εV2=εV0=0.9%，两种方法的误差计算结果，如表1所示.

由表1可知，在三相电压、电流不对称时“电压替代法”计算的退补电量误差远小于“更正系数法”的误差.按简化公式(14)计算误差也不超过2.4%，如按公式(9)计算，由于各相序相差不同，不能同时为1或-1，有时还能正负相抵，误差更小.同时，也可以看出随着C相电流KI的增大，A相失压更正电量的误差值越来越小，这与图3误差变化曲线分析所得出的结论相一致.

5 现场应用效果对比

基于本文所提方法，以上述某实际电网#1计量点为例，在现场对三相四线电能表样机模拟A相失压故障，原电能表正常运行.在2015年8月3日零点至8月13日10点期间，样机和原电能表的电量、电流、电压、功率等数据均正常监测.

表2 某实际电网#1变误差计算

从表2的误差数据可见，该段期间样表的故障计算表码为22.11 kWh，退补计算表码为18.94 kWh，合计共41.05 kWh，与原计费电表的计算表码40.96 kWh相比，相对误差为0.22%.样机现场应用效果明显接近于未发生故障时的电能表的计算表码，得到的结果也充分的验证了电压替代法退补电量的精确度远优于传统人工计算退补电量的方法.

6 结术语

本文采用“对称分量法”对“电压替代法”退补电量的更正功率误差进行了分析计算，导出三相四线电能表失压退补电量的更正功率在电网三相电压、电流不平衡状态下的误差表达式.利用误差表达式计算了三种不平衡条件下的误差值，并通过实例比较了C相电流取不同电流时，“电压替代法”和“更正系数法”的更正功率计算误差，结果表明在三相不平衡负荷下“电压替代法”计算的退补电量误差远小于“更正系数法”的误差.建议正常时监测记录电网电压、电流的不平衡范围，失压时根据公式(14)计算的更正功率误差范围，使该方法进一步严谨完善.