内齿盘-齿块锁止机构运动干涉及修形的研究
2018-07-19鄂瑞迪赵自强李党生王文中
鄂瑞迪,赵自强,李党生,王文中
(1.北京理工大学 机械与车辆学院,北京 100081;2.浙江龙生汽车部件股份有限公司,浙江 杭州 311500)
1 引言
汽车座椅调角器是座椅靠背和底座之间的主要承力部件,人体作用在靠背的力完全由调角器的锁止机构承担。为保证乘员的安全,尤其是在汽车碰撞时座椅不至于拉脱,调角器需要保证一定的锁止可靠性[1-2]。而调角器是汽车座椅的关键性部件,核心技术一直被发达国家垄断[3]。调角器的核心技术在于齿形的参数设计与制造,在齿形设计方面没有任何可直接效仿的程式。
汽车座椅调角器核心件锁止机构通常采用齿块-内齿盘结构,如图1所示。其工作原理为:齿块只能进行径向运动,内齿盘只能进行周向转动;在非锁止状态下内齿盘与齿块脱离啮合状态,内齿盘可自由转动实现座椅靠背角度调节运动;在锁止状态下,齿块径向锁入内齿盘中,内齿盘和齿块相互啮合,内齿盘不能自由转动,座椅处于锁止状态。

图1 汽车座椅调角器核心件的位置Fig.1 The Position of Automobile Seat Recliner
在齿块径向锁入的过程中,如图2所示。1号齿和2号齿可以正确的锁入到内齿盘的1号齿槽和2号齿槽中,而3号齿和4号齿则会被内齿盘对应啮合齿的顶部阻挡,导致齿块无法沿径向锁入到正确的啮合位置,产生所谓的径向锁入干涉现象[4]。当汽车座椅调角器核心件在实际使用过程中出现这种运动干涉现象时,齿块和内齿盘就不能完全啮合。由于齿块和内齿盘处于半啮合状态,有效承载部分明显减少,汽车座椅靠背极易出现锁止失效的情况,使得汽车在发生碰撞时座椅约束不足对乘客造成伤害。为了避免运动干涉,在分析齿块沿径向啮入过程中的几何干涉条件的基础上,提出了一种啮合齿修形的方法。由于调节角度的过程中,内齿盘做圆周运动并必须能够在任意角度锁止,内齿盘的各个齿形需要保持一致。因此,修形主要是针对齿块各齿进行[5]。
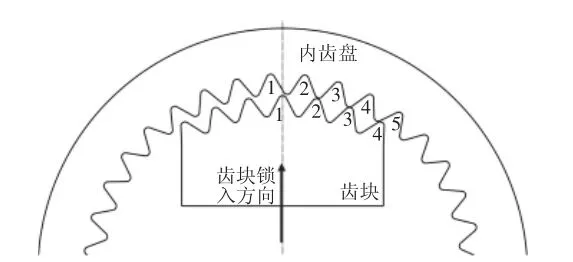
图2 径向锁入干涉现象Fig.2 The Phenomenon of Radial Locking
2 干涉分析和避免运动干涉的条件
在调角器实际锁入过程中,与内齿盘同时接触的齿有时不止一个,如图3所示(图中用半径为r的圆代表齿块的齿顶)。齿块沿径向与齿盘进入啮合的过程中,其相对位置可能出现以下三种情况:(1)齿块所有与内齿盘接触的齿均在与之接触的齿的同侧,如图3(a)所示。可正常锁入完成啮合;(2)除了处于同侧的齿,如图3(b)所示。齿块中存在齿与内齿盘的齿顶圆相切,即,两齿的接触压力方向与内齿盘的运动方向垂直[6],但是由于齿盘可以转动,因此也可正常锁止;(3)齿块中存在任意两个齿分别位于内齿盘两个齿的不同侧,如图3(c)所示。导致齿块对齿盘产生了方向相反的转动力矩,齿块运动受到干涉,造成不能锁止到位。

图3 齿块多个齿与内齿盘接触位置Fig.3 The Contact Position Between the Teeth of Gear Blocks and the Inner Gear Disc
因此,如图4所示,为避免齿块径向锁入时发生干涉,对于任意的α∈[0,2π/z),齿块上所有齿顶的倒角中心应位于齿盘中心与齿盘齿倒角中心连线的同一侧,即图4中虚线的同一侧。虚线O0Oout-i的方程为:

为避免齿块沿径向与齿盘啮合过程中发生干涉,由几何关系可知,齿块上所有齿顶的倒角圆心坐标应满足以下条件:

式中:z—内齿盘齿数,i=1,2,3,…,j=1,2,3,…;O0—内齿盘几何中心;Oout-i—内齿盘上第i个齿的齿顶倒角圆心;Oin-i—与内齿盘第i个齿接触的齿块齿的齿顶倒角圆心,当判别式(2)取等号时对应图3(b)的临界状态。

图4 齿块齿与齿盘齿相对位置关系Fig.4 The Position of Gear Blocks’Teeth and Inner Gear Disc’s Teeth
3 避免运动干涉的齿廓修形量的计算
由以上分析可知,齿块沿径向与齿盘进入啮合的过程中可能会产生干涉,导致产生不能锁止的情况,因此需要对齿块进行修形以避免运动干涉,且修形后应保证齿块上的齿仍具有足够的强度,为此应尽量保证齿块内侧齿廓与内齿盘齿槽为面接触以增加承载面积,齿块外侧齿廓与内齿盘齿槽线接触,此处定义靠近齿块中心的齿侧为内侧齿廓,远离齿块中心的齿侧为外侧齿廓。齿块与内齿盘完全啮合时齿块啮合齿倒角圆心沿着内齿盘齿面平移di,如图5所示。di即为每个齿的修形量(图5中为齿2的修形量d2)。

图5 齿廓修形量Fig.5 The Modification Value of the Teeth Profile
首先,齿块、内齿盘啮合机构是对称机构,因此,修形量计算只需考虑齿块的右半部,左半部可以根据对称面进行镜像获得。设计时,齿块从最中间的齿开始逐个修形,每完成一个齿的修形,添加下一个齿的齿廓。定义齿块正中间的齿为第1齿,对于任意的α∈[0,2π/z),各齿相对位置应满足式的条件才能避免发生啮入干涉。当考虑齿块前两个齿的时候,内齿盘与之相对应的齿顶倒角圆心Oout-i的坐标为:
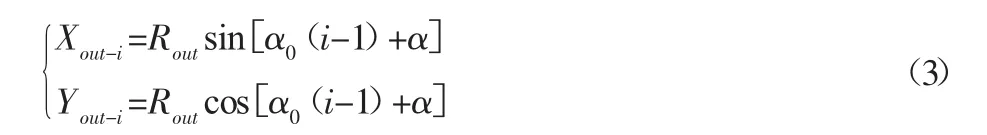
式中:i=1,2—内齿盘第一个齿和第二个齿的齿顶倒角圆心,如图5所示。Rout—内齿盘齿顶倒角圆心轨迹圆半径;相邻两齿的间隔角为α0=2π/z;α—直线Oout-1O0与Y轴夹角,定义了齿盘与齿块的相对位置,如图4所示。
由几何分析可知,齿块上第i齿的齿顶倒角圆心坐标[7]为:

式中:i=1,2,分别代表齿块中间右侧第一个齿和第二个齿的齿顶倒角圆心;s—修形前的齿高,s=Rin-Rout+2r;Rin—齿块修形前齿顶倒角圆心轨迹圆半径;r—内齿盘齿顶倒角半径;u—齿块的锁入位移,当α=0时,u=0,内齿盘第一齿与齿块第一齿的齿顶倒角圆心均在Y轴上,其圆心距Oout-1Oin-1=2r,而内齿盘第二个齿与齿块第二个齿的圆心距Oout-2Oin-2>2r。之后随着径向锁入运动α逐渐增大,u也逐渐增大,直到齿块第二齿与内齿盘的对应齿相接触,此时Oout-1Oin-1=Oout-2Oin-2=2r,将Oout-1、Oin-1、Oout-2、Oin-2坐标代入后得到式(5)和式(6)。
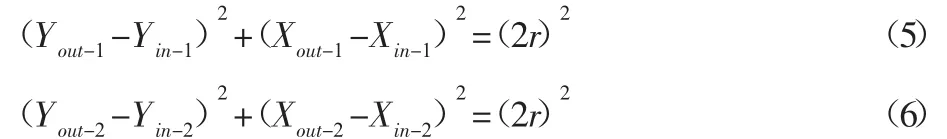
由式(3)、式(4)、式(5)、式(6)可求得 Oout-1、Oin-1、Oout-2、Oin-2四点的坐标值,代入到式(2)中,判断各齿相对位置是否满足式(2)的条件,如不满足则需要对第2齿进行修形计算。设Oin-2点的修形量为d2,其修形后的点命名为O′in-2,其最小修形量由式(2)可得,即判别式取等号所对应的临界状态(图3b)时所需修形量最小,令:

4 结果分析
以某型号汽车座椅调角器核心件为例,其基本参数,如表1所示。根据之前关于修形量的计算分析,编写程序,计算结果解析解修形量d,如表2所示。之后根据几何原理,运用商业软件CATIA草图绘制模块用图解法对齿廓进行了绘制并修形,所得结果图解法修形量d,如表2所示。由表2可知,齿块上随着各齿离中间齿的距离增加所需要的修形量d逐渐增加;相对于修形前的各齿高度s(=2r+Rin-Rout=0.47147),各齿的修形量所占比例较小,各齿高度改变不大。

表1 内齿盘与齿块设计参数Tab.1 The Gear Blocks and Inner Gear Disc Design Parameters
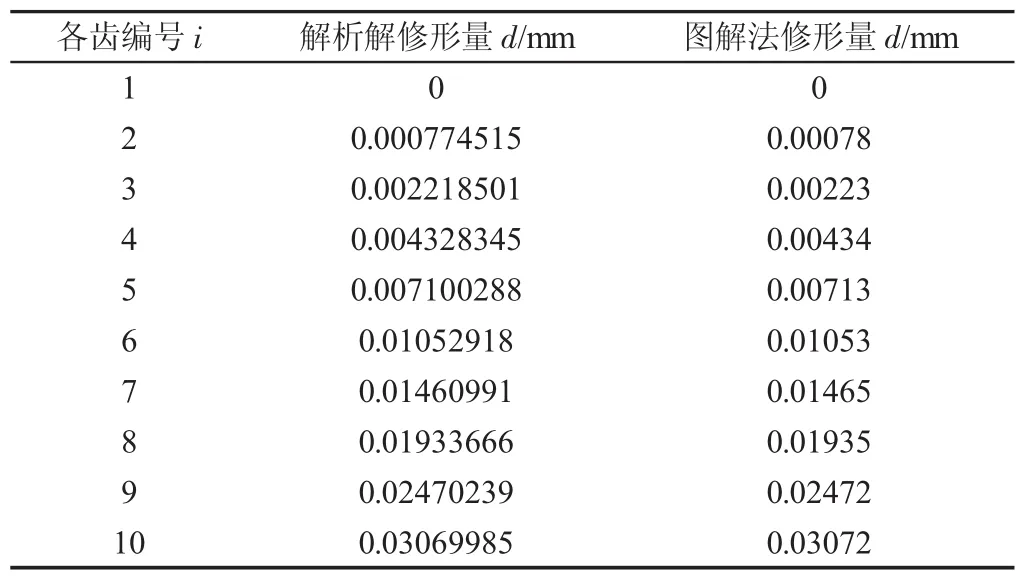
表2 各齿修形量计算结果Tab.2 The Results of Tooth Profile Modification
4.1 齿块齿修形对机构运动的影响
为了验证齿块修形是否能避免齿块径向啮入过程可能发生的干涉,通过有限元建模对修形后的齿块-内齿盘锁止机构进行运动仿真[8](即图1所示的非锁止状态运动到锁止状态,内齿盘圆心固定不动,内齿盘可绕其圆心在XY平面内转动,齿块沿Y轴正向运动),计算结果,如表3所示。分析结果表明:优化前α≤0.3°时就会发生锁入运动干涉现象,齿块无法完全锁入到内齿盘中,优化后内齿盘在任意初始位置,齿块的锁入运动干涉现象都得到有效避免。

表3 齿块径向啮入过程有限元分析结果统计Tab.3 The Results of Finite Element Analysis During Locking Process
4.2 齿块齿修形对锁止机构承载能力的影响
由图5可见,齿块齿修形导致齿高有所减小,齿顶厚度有所减薄,可能会影响其承载能力。为了检查齿块齿的修形对锁止机构的承载能力的影响,针对锁止状态(工作承载状态)进行有限元分析[8-9],如图1所示。对内齿盘施加逆时针方向(图6箭头所示方向)转矩2000N/m,齿块在支撑部件作用下静止不动以承担载荷,如图6所示。结果表明:修形前,齿块只有右边四个齿为主要承载齿,超过屈服极限的区域较集中;修形后齿块上大部分齿参与啮合,使得齿块上各齿载荷分布比较均匀,超过屈服极限的区域明显减小,修形后由于参与啮合齿数增加,承载能力得到提高。
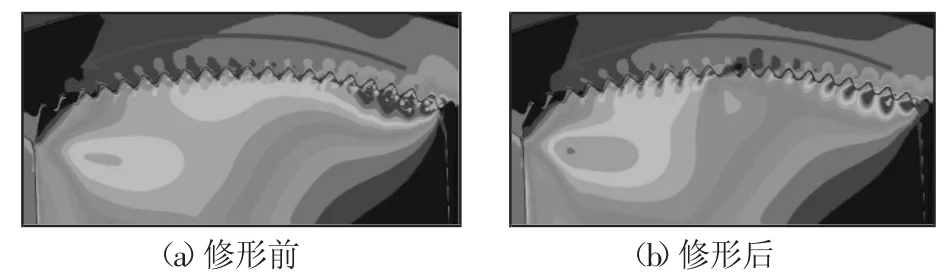
图6 锁止状态下的承载能力Fig.6 The Load Carrying Capacity Under Locking Condition
5 结论
针对内齿盘-齿块径向锁止机构在啮入过程中发生的运动干涉问题,基于几何原理分析得到了干涉发生的条件,提出了避免干涉的措施,主要结论如下:(1)提出了内齿盘-齿块锁止机构在齿块径向啮入过程中发生齿廓干涉的判别式;(2)提出了通过齿块齿修形避免内齿盘-齿块机构在径向啮入过程中发生齿廓干涉的方法,发展了避免齿廓重叠干涉的最小修形量的计算方法;(3)通过有限元仿真分析,验证了齿修形的方法有效避免了齿廓重叠干涉现象,且能够提高承载能力。
