拓扑修形齿轮副传动特性仿真分析与试验

王会良，曹杨麒

（河南科技大学 机电工程学院，河南 洛阳 471003）

1 引言

齿轮传动系统被广泛应用于机械制造业中，对于整套设备的运行，它的工作性能和力学特性都起到关键的影响。提升齿轮承载能力与减小振动噪声已经成为改善齿轮质量的关键技术之一。但是，由于齿轮副工作中啮合力不断发生变化，造成了齿轮之间的干涉，不可避免地产生啮入、啮出冲击，进而造成传动精度、齿面载荷的变化和传递误差的产生[1-2]。

通过大量研究和实践生产发现，只依靠齿轮制造精度的提升来应对齿轮性能要求日益增长的高标准是远不够的，还会大大增加传动机构的制造成本，轮齿修形对改善传动的平稳性及延长工作寿命有着明显的效果[3-4]。国内学者利用齿轮传动系统做了一些仿真和优化分析。文献[5]在齿轮修形理论的基础上配合使用Romax wind出色的载荷分布分析功能，在等效载荷下对齿轮箱箱体进行静力学仿真，依据载荷分布情况、传动误差等参数，对齿廓与齿向的修行长度和曲线以及修形量进行分析、确定。文献[6]在Romax平台下，研究了拖拉机变速箱传动系统，对修形后齿轮的传递误差曲线和啮合特性进行分析，比较修形前后齿轮的振动特性，证明了修形效果的有效性。文献[7]通过对某5MT变速器传动误差、载荷分布、接触和弯曲安全系数的仿真分析，找到设计中存在的不足，进而采用齿轮微观几何修形的方法改善了这些特性。文献[8]对细高齿齿轮进行优化修形，减小了传动误差，使传动系统的运行更加平稳。文献[9]针对NGW31齿轮箱箱体建立三维模型，通过有限元模态分析，得出避免共振频率的发生可以为齿轮箱达到减振降噪的结论。

因此，以某齿轮箱两级齿轮传动系统为研究对象，构建其三维模型，并根据实际情况添加相关约束，进行仿真分析，获得传动系统各级齿轮的安全系数、接触和弯曲应力等数据。对比修形前后传动系统的传递误差，载荷分布等传动特性，最后搭建试验平台，对未修形和修形齿轮进行振动测试，比较修形前后齿轮的振动信号频谱图。研究结论表明基于拓扑修形的优化设计，对齿轮传动特性和承载能力的提高能够起到有效作用。

2 齿面拓扑修形

2.1 齿轮修形的理论与方法

根据齿轮的静态传递误差直接影响传动过程中的振动和噪声，为了能够减小传动系统的动载荷，降低齿轮振动噪声，常用的方法是尽可能地减小静态传递误差的变化幅值。通过对轮齿的修形，可以降低齿轮静态传递误差幅值，从而能够实现减小传动系统振动的目的，同时可以提高齿轮传动的动态性能，减少啮合撞击和干涉，使齿面的润滑状态得到改善。

按照轮齿修形所处部位的不同，修形方法包括齿向修形和齿廓修形，沿齿廓、齿向方向上同时进行三维综合修形的方法称为拓扑修形，它是两种修形方法的合理组合。拓扑修形轮齿表面，如图1所示[10]。图中：Σ1—理论渐开线齿面；Σ2—拓扑修形齿面。其中区域①为渐开线齿面，砂轮没有径向进给运动，并按标准渐开线齿廓来对相应砂轮廓形求解，同时；区域②、区域④、区域⑥、区域⑧为齿向和齿廓双向修形；区域⑤和区域⑨为齿向单向修形；区域③和区域⑦为齿廓单向修形。图中 a、b、c、d、e、f、h、j为各区域之间的边界线，ue、ud、uc和 ua分别是齿廓修形边界线 e、d、c、f渐开线处的展开角，θ0、θa、θb和 θmax分别为齿向修形边界线 h、a、b、j处齿轮转角。通过控制齿廓修形边界线和齿向修形边界线处相对应的渐开线展开角和齿轮转角的大小来实现齿面拓扑区域边界的划分。

图1 拓扑修形齿面Fig.1 Topological Modification Tooth Surface

通过在渐开线的发生线上叠加一个修形量ΔL，同时对齿面进行修根和修缘，这种方法称为齿廓分段修形。修形量与展开角成一抛物线函数关系，齿廓分段修形量方程为：

式中：amp—沿齿廓方向修形的固定系数；rb—基圆半径；u1—渐开线展开角；ue、ua—齿顶和齿根渐开线在端面处齿廓方向上的展开角。

齿向修形指在啮合齿线方向上，对轮齿表面做细微的修整，经过修形的齿面相对于理论齿面产生一定的偏移，其修形量计算公式为：

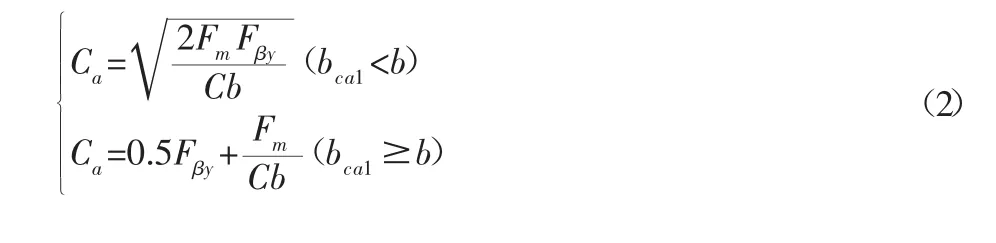
式中：Ca—鼓形量；C—啮合综合刚度；b—齿宽；bca1—有效接触宽度；Fm—圆周力；Fβy—啮合齿向误差。

2.2 齿轮修形量的设计

主要采用齿向的斜度修形和齿廓齿顶修缘的抛物线修形相结合的方式，即拓扑修形来进行优化设计。在Romax中利用微观几何修形工具对轮齿进行修整，结合各种修形曲线，如鼓形量，抛物线，线性斜度等，再通过式（1）、式（2）计算分析，求得最优综合曲线。经过多次比较分析得到，齿向斜度修形量是-10.1μm，抛物线修形量是7μm，最优综合曲线，如图2（a）所示；齿廓方向的修鼓量为5μm，齿顶修缘部分的抛物线型修整量为28μm，最优综合曲线，如图 2（b）所示。

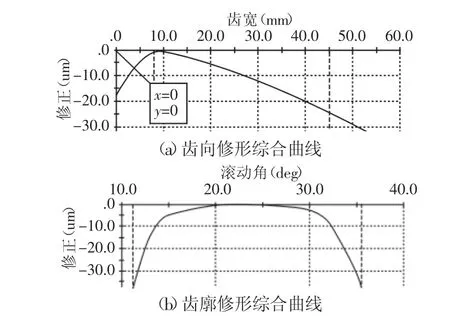
图2 齿轮修形综合曲线Fig.2 Gear Modification Resultant Curve

3 传动系统模型的建立

某齿轮箱传动机构各级齿轮详细设计参数，如表1所示。它由输入轴、中间轴、输出轴组成，依靠两对外啮合斜齿轮副进行传动，一级齿轮副由主动轮1和从动轮2组成，二级齿轮副由主动轮3和从动轮4组成。在Romax环境中，根据表1中各级基本参数，建立三维仿真模型，如图3所示。

表1 各级齿轮的基本参数Tab.1 Basic Parameters of Gears at All Levels

齿轮材料选择45钢，调质后表面进行淬火处理，芯部硬度为240HBS，齿面硬度为250HBS。齿轮的许用弯曲应力计算公式如下：

式中：ZN—接触疲劳寿命系数；σHlim—接触疲劳极限；SH—接触疲劳强度安全系数。

式中：YN—弯曲疲劳寿命系数；σFlim—弯曲疲劳极限；SF—弯曲疲劳强度安全系数。

根据以上公式计算得到 [σH]为600MPa，[σF]为1500MPa。

图3 传动系统仿真模型Fig．3 Transmission System Simulation Model

4 齿轮传动系统的传动特性分析

4.1 传动系统静态分析

建立齿轮传动系统虚拟样机，设置齿轮箱工作温度为70℃，设定输入转速为1000r/m，额定功率为120kW，工作时间为100hrs。强度校核标准为ISO6336：2006，运行设定好的循环工况，进行静态分析得到齿轮的最大接触应力、最大弯曲应力和安全系数结果，如图4（a）所示。所有齿轮的损伤百分比都较小，预测计算寿命都较长，达到设计要求。

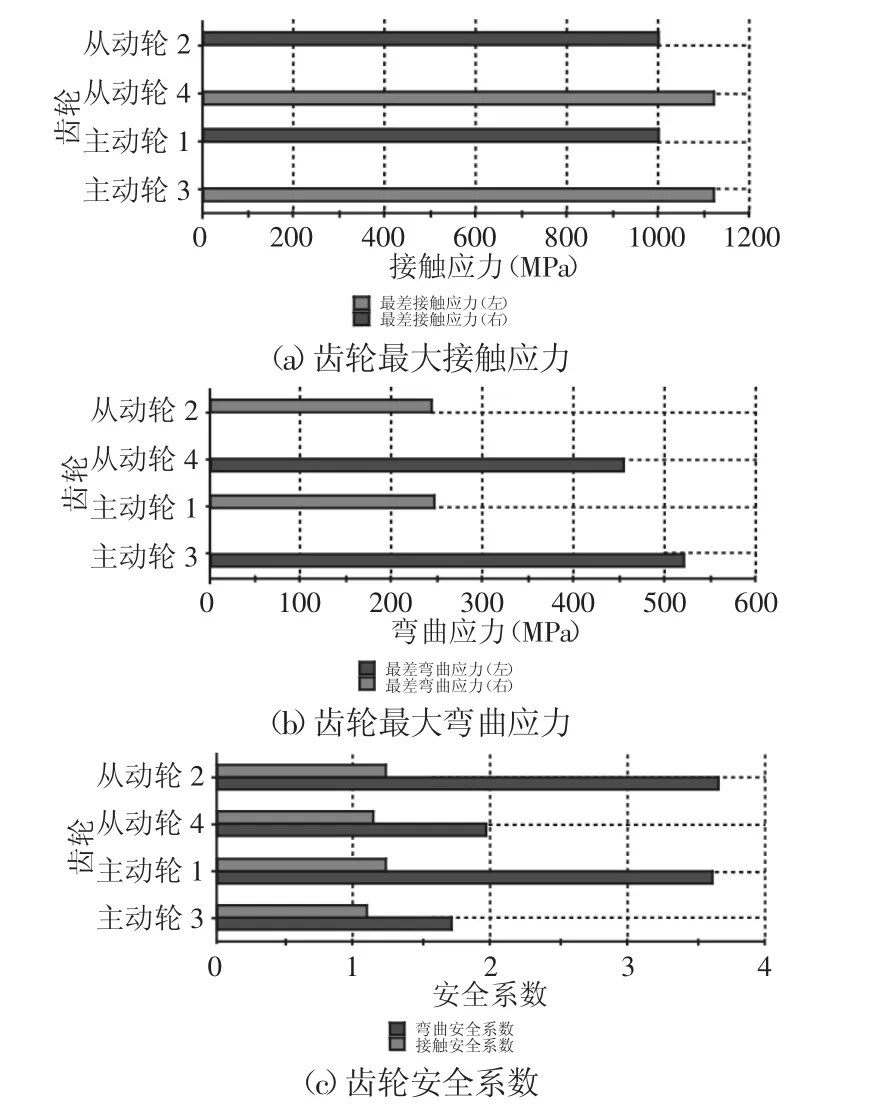
图4 静态分析结果Fig．4 Static Analysis Results

为了方便结果的记录分析，将计算分析详细数据整理成表2。各级主、从动轮的接触安全系数都不小于1，如表2所示。各级主、从动轮弯曲安全系数都在（1．5～4）之间，安全系数值均大于在分析设置时所设定的值，同时也都在合理的范围之内。第一级、二级齿轮副的最大接触应力分别为 1004．135MPa，1119．052MPa，都小于材料的许用值；第一级、二级齿轮副的最大弯曲应力分别为246．931MPa，520．663MPa，也都小于材料的许用值。所有的接触应力值和弯曲应力值均满足静力学使用要求，验证了传动系统设计的安全性。

表2 各级齿轮的静态分析结果Tab.2 Contact Static Analysis Results

4.2 传动系统动态分析

经过传动系统的静应力分析，得到其静态特性满足设计要求；但由于系统自身存在不可避免的刚度变化和受力变形，在高速下运行工作时会产生较大的冲击载荷和振动噪声，从而降低系统的承载能力，影响其工作性能，严重的可能破坏系统中的零部件，造成整体工作失效。所以为了保证系统的稳定运行，还需要分析其动态性能。主要从传动误差和载荷分布两方面来做分析。

动态激励包括内部激励与外部激励，而内部激励主要变现为传动误差。传动误差是指主动轮转动任意角度，从动轮理论传动角度数和实际传动角度数的差值，以节点处角位移和线位移来描述，用公式表达如下：

式中：θ1—主动轮理论传动角度；θ2—从动轮理论传动角度；rb1—主动轮半径；rb2—从动轮半径。在现实加工工艺进程里，安装误差与啮合冲击都会起到一定的影响，因此式（5）左右两边并不完全等值，从动轮实际传动角度可以表示为：

式中：ε—从动轮实际传动角度；Δθ2—传动误差产生的角度偏差值。

式中：TE—传动误差。

传动误差分析对于动态分析具有重要的意义。图5（a）和图5（b）分别表示利用动态分析功能模块绘制出的一级齿轮副修形前后传动误差曲线，得出实际啮合线对比理论啮合线随滚动角大小改变的偏移量。啮合线上最大位移量和最小位移量的差值即为传动误差，根据图中数据计算得到齿轮副修形后的传动误差值为2．3μm，未修形的值为 6．37μm，修形后传动误差值比修形前下降了63．9%。比较发现经过修形后的传动误差曲线比初始未修形传动误差曲线的波动性小很多，曲线中急剧变化的情况都消失了。传动误差做为影响齿轮精度和传动稳定性的主要因素，即啮合线最大偏移量与最小偏移量差值越低，就越能更加稳定的传动。

图5 一级齿轮副传动误差曲线Fig．5 Transmission Error Curve of First Grade Gear Pair

借助微观几何分析模块，对主动轮1进行研究，施加同等载荷，得到其修形前和修形后齿面载荷分布情况，如图6、图7所示。可以看出最小单位长度分布载荷由119N/mm降低到0N/mm，加载面偏载现象和边缘接触现象依次消失，修形后沿齿宽方向的最大值从齿面端部向齿面中部转移，其齿轮单位啮合长度的载荷分布明显得到改善，虽然单位长度最大载荷略微增大，但整个齿宽方向载荷分布更均匀了，且最大载荷主要集中在中间部位，由于中间承载能力最强，所以不会对齿面造成明显影响。齿廓方向受力主要集中在中间部位，齿根和齿顶的单位长度载荷很小，这样在轮齿开始啮合和退出啮合时所受的冲击力会大大减小，使齿轮传动更平稳。

图6 主动轮1未修形载荷分布图Fig.6 Load Distribution of the Active Gear 1

图7 主动轮1修形后载荷分布图Fig.7 Load Distribution of the Modification Active Gear 1

5 传动系统的振动试验

图8 齿轮振动测试加载试验台Fig.8 Gear Vibration Test Loading Test Bench

仅靠理论分析不能完全了解传动系统的振动特性，为了进一步验证修形结果的正确性，通过振动试验获取振动信号数据是一个不可或缺的手段。先将修形前齿轮副安装于齿轮箱内进行加载试验，经过修形后，再次对齿轮副加载试验。振动试验台由齿轮箱箱体、变频电动机、加速度传感器、扭矩传感器、磁粉制动器、声压计等装置组成，如图10所示。变频电机输出不同档位的转速，并通过磁粉制动器加载一定载荷，利用加速度传感器来测不同位置的振动信号。针对齿轮副，试验3个档位，将电动机3个档位速度设定为1000r/min、850r/min、650r/min，加载试验的主要参数，如表3所示。

表3 振动试验的主要参数Tab.3 Main Parameters of Vibration Test

在已搭建完成测试平台上进行加载试验，采集加速度振动信号数据，对这些数据借助动态信号处理软件做频谱分析，得到齿轮修形前后的试验结果。当电机转动速度为1000r/min时的齿轮振动信号频谱图，如图9所示。

图9 齿轮振动信号频谱图Fig.9 Gear Vibration Signal Spectrum

由加载试验后的振动频谱图可知，未修形齿轮在频率约为220Hz、578Hz、804Hz 处的振动加速度幅值分别为 0.0115g、0.0035g、0.0018g；修形齿轮在频率为 220Hz、578Hz、804Hz处的振动加速度幅值分别为0.0021g、0.0029g、0.0015g；比修形前的幅值都有所降低。而且对比频谱图可以看出，修形前齿轮振动加速度频谱率更加复杂，且具有多峰值特性；修形后的齿轮振动加速度没有明显的高幅值谐波，整体振动幅值明显降低，各种谐频成分明显减少，振动能量也明显下降。另外由声压计的测量数据显示，修形后传动系统的振动和噪声略有下降，与传递误差最大波动值下降使振动噪声降低的结论相吻合。说明齿轮的微观拓扑修形，对降低传递误差最大波动值引起振动噪声降低的有效性，从而证明了传递误差分析结果与修形方法是正确可行的。

6 结论

基于Romax提供的虚拟建模和仿真平台，完成对某两级齿轮传动系统三维模型的创建。根据实际情况添加相关约束，在给定的工况下，对其进行了静态分析和动态分析以及振动试验。通过这些研究分析得到如下相关结论：（1）利用静应力分析，验证整个机械传动系统结构强度分布合理，满足静强度的要求，且存在一定的安全余量。齿轮的工作疲劳寿命都达到要求的水平，从而证明设计合理可靠。（2）对一级齿轮副进行动态性能分析，得到其修形前后的传动误差曲线，以及轮齿表面载荷的分布情况。对比发现齿轮修形有效地降低了传递误差，齿面的受力分布情况得到极大改善，齿轮的工作传动更加稳定、承载能力及设计水平也都得到相应提升。（3）利用传动系统的振动试验，借助软件来处理分析测试得到的振动加速度信号数据，结果表明拓扑修形同时兼具两种基本修形方式的优点，降低了齿轮的振动和噪声，从而验证齿轮修形的有效性和正确性，为进一步齿轮数字化设计制造提供了一定的理论依据和参考价值。