大负载纵弯谐振变幅器谐振特性的研究与试验
2018-07-19秦慧斌付俊帆
吴 霄 ,秦慧斌 ,,付俊帆 ,吕 明
(1.中北大学 先进制造技术山西省重点实验室,山西 太原 030051;2.太原理工大学 精密加工山西省重点实验室,山西 太原 030024)
1 引言
对于硬脆难加工材料,超声加工能显著降低切削力,改善工件表面质量,提高加工效率和刀具寿命,在陶瓷、玻璃、钛合金、淬火钢等硬脆材料的车、铣、磨、钻削加工方面应用广泛[1]。谐振系统是超声加工工艺系统的核心,其性能直接影响着加工质量。超声振动系统一般由超声波发生器、换能器、传振杆、变幅杆和加工工具或工件等组成。通过调节超声波发生器的频率使振动系统谐振于设计频率,获得良好的加工工艺效果。功率超声纵弯谐振变幅器是一种典型的复合振动模式的变幅器,换能器和变幅杆纵向振动激励环盘负载作节圆型横向弯曲振动,完成两种不同振动类型的耦合。纵弯谐振变幅器具有优良的特性,在旋转超声加工、超声清洗、金属疲劳检测等领域应用广泛[2-4]。
文献[5]最早提出了由变幅杆与大负载环盘组成的纵弯谐振变幅器。文献[6]对弯曲振动圆盘振动特性进行了试验研究。文献[7]
来稿日期:2018-02-06
基金项目:先进制造技术山西省重点实验室开放基金项目(XJZZ201603);精密加工山西省重点实验室开放基金(201601);中北大学研究生科技基金(20161311)
作者简介:吴 霄,(1993-)男,山西长治人,硕士研究生,主要研究方向:超声振动精密加工技术;
秦慧斌,(1978-)男,山西长治人,博士研究生,副教授,主要研究方向:齿轮超声振动精密加工技术设计了一种纵弯谐振水声换能器,扩大了换能器带宽。文献[8]提出了阶梯齿轮变幅器纵弯谐振的统一求解模型。文献[9]利用有限元法,研究了纵振激励频率对圆盘弯曲振动特性的影响。文献[10]提出了一种新型纵弯转换超声振动雾化系统,研究了由换能器、变幅杆与工具组成的振动系统的各种谐振状态特性。上述文献都是对均质材料纵弯谐振变幅器进行研究,且负载较小,很少对大负载多材料纵弯谐振变幅器进行研究。
以三环盘与变幅杆组成的变幅器为例,基于Mindlin中厚板理论,建立纵弯谐振变幅器的振动模型,推导出频率方程与振型解析表达式,通过阻抗分析试验和超声谐振试验对变幅器的谐振特性进行了对比研究,为超声谐振系统的设计与应用提供了技术参考。
2 纵弯谐振超声变幅器理论模型
功率超声纵弯谐振变幅器由变幅杆和大负载环盘组成,实验所用变幅器结构,如图1所示。大负载环盘由不同材料的环盘1、2、3组成,中性面为同一平面。环盘中心孔与圆锥变幅杆芯轴通过紧固螺母刚性连接。紧固螺母与变幅杆芯轴的尺寸相对变幅器较小,在理论分析中可以忽略。
以变幅杆大端中心点为原点,以变幅杆中心轴线为z轴,建立图 1 所示的(r,θ,z)圆柱坐标系。R1、R2分别表示圆锥变幅杆大端、小端半径,L 表示变幅杆长度。R3、R4、R5分别表示环盘 1、2、3的内径,R6表示环盘 3 的外径。t1、t2、t3分别表示环盘 1、2、3 的厚度。由于变幅杆和各个环盘的材料不同,故分别以ρ1、ρ2、ρ3和ρ4表示环盘 1、2、3 和变幅杆的密度,E1、E2、E3和 E4表示环盘 1、2、3和变幅杆的弹性模量,μ1、μ2、μ3表示环盘 1、2、3 的泊松比。
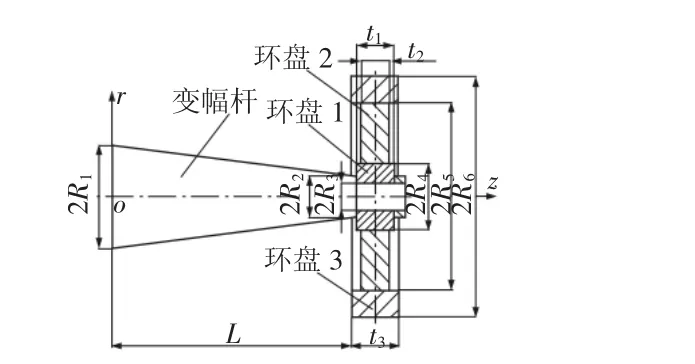
图1 纵弯谐振变幅器结构示意图Fig.1 Structure of Longitudinal-Flexural Resonance Transducer
当变幅器作纵弯谐振时,变幅杆纵向振动,其纵向位移ξ的解析表达式为:

式中:圆波数k=ω/c,圆频率ω=2πf,变幅杆的纵波波速c=(E4/ρ4)1/2;C1、C2—待定常数。
基于Mindlin理论,单个环盘的径向弯矩分量Mri和径向剪力分量Qri的解析表达式为:


式中:Aji、Bji(j=1,2;i=1,2,3)为待定常数;Jn(·)、Yn(·)—第一类、第二类贝塞尔函数。当环盘负载作节圆型横向弯曲振动时,节径数为零(即n=0)。
将式(3)带入式(2),可得径向弯矩分量Mri和径向剪力分量Qri的表达式为:

当变幅器作纵弯谐振时,变幅杆大端纵向振动,应力为零,故有自由边界条件
变幅杆小端与环盘接触面上存在有沿z轴方向的力与位移的连续条件;由于环盘无径向转动,故在r=R3处,环盘1的径向转角 βr1为 0,即:
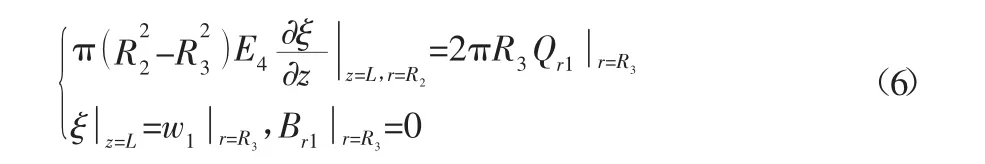
环盘2分别与环盘1在r=R4处,和环盘3在r=R5处满足横向位移wi、径向转角βri、径向弯矩分量Mri和径向剪力分量Qri的连续条件:
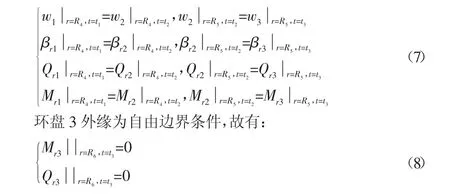
将式(1)和式(4)~式(5)带入式(6)~式(8)并整理,可得齐次方程组:Δ14×14ξ14×1=014×1,当待定常数不全为 0 时,其充要条件:

式(9)即为纵弯谐振变幅器的频率方程。
变幅杆大端振幅与换能器的输出振幅ξ0相等,即有纵向位移的边界条件联立此边界条件与齐次方程组可得一个超静定方程组。通过求解该超静定方程,可求得ζ14×1的一组特解。将该特解带入式(4),可得:

式(10)即为纵弯谐振变幅器的振型解析表达式。
3 纵弯谐振变幅器阻抗分析试验
根据纵弯谐振变幅器频率方程,设计了两个纵弯谐振变幅器。变幅器1由45钢变幅杆与黄铜H62阶梯环盘组成,设计频率为20kHz;变幅器2由45钢变幅杆和灰铸铁HT200阶梯环盘组成,设计频率为20kHz。变幅杆和三环盘的材料性能参数,如表1所示。变幅杆杆长L为未知尺寸,变幅器其他尺寸由加工工艺和设备决定,如表2所示。采用Matlab进行编程求解,结果为L1=114.6mm,L2=189.4mm。

表1 材料性能参数Tab.1 Material Mechanical Properties

表2 纵弯谐振变幅器尺寸参数与设计频率Tab.2 Parameters and Design Frequencies of Longitudinal-Flexural Resonance Transducers
变幅杆大端与YP-5520-4Z柱型换能器相连,换能器最大振幅为6μm,因此变幅杆大端振幅ξ0=6μm。将其带入式(10)并求解,可得 ζ10×1的解,将其代入式(3),求解可得三环盘的振幅:黄铜H62阶梯环盘在半径r=28.58mm、r=54.18mm和r=74.64mm处为零振幅,灰铸铁HT200的阶梯环盘在半径r=48.86mm和r=72.96mm处为零振幅,即此处为三环盘的振动节圆位置。
将变幅器和换能器分别与传振杆的上下端相连,并在连接面上涂抹凡士林填充两者之间的微小间隙,减小超声波在连接面的反射损失。用导线将阻抗分析仪PV70A与超声换能器相连接,如图2所示。利用相应软件测量变幅器的纵弯谐振频率,测量结果如表3中fE行所示。

图2 变幅器阻抗分析试验Fig.2 Impedance Analysis Experiment of Transducers

表3 不同方法求得的纵弯谐振频率的比较Tab.3 Comparison of Longitudinal-Flexural Resonance Frequency Obtained by Different Means
由表3可知,试验频率的最大误差为2.75%。因此阻抗分析试验得到的纵弯谐振频率结果与设计频率基本一致,证明了上述的纵弯谐振变幅器设计方法对工程设计具有一定的参考意义。
4 纵弯谐振变幅器谐振试验
将变幅器与换能器安装在试验台上,换能器与ZJS-2000型超声波发生器相连,组成超声谐振试验装置,如图3所示。在环盘表面上撒上碳化硅颗粒,打开超声发生器并调节调频螺母,当超声发生器的频率分别为20990Hz和20640Hz时,碳化硅颗粒聚集为圆环,如图4所示。表明三环盘在变幅杆纵向振动的激励下作节圆型横向弯曲振动,即变幅器作纵弯谐振。变幅器1与变幅器2谐振频率与设计频率之间的误差分别为4.95%和3.20%。

图3 超声谐振试验装置Fig.3 Experiment Equipment of Ultrasonic Resonance

图4 变幅器纵弯谐振试验结果Fig.4 Test Results of Longitudinal-Flexural Resonance of Transducers
利用PDV100型激光测振仪对环盘振幅进行测量,得到三环盘端面振幅曲线,如图5所示。理论计算和试验得到两种环盘振幅曲线的对比,如图6所示。两种方法得到的三环盘振幅曲线的整体形态基本一致。对于振幅曲线的零振幅位置,黄铜H62阶梯环盘实验振幅曲线与理论计算最大偏差为6.51%,灰铸铁HT200阶梯环盘实验振幅曲线与理论计算最大偏差为3.56%。
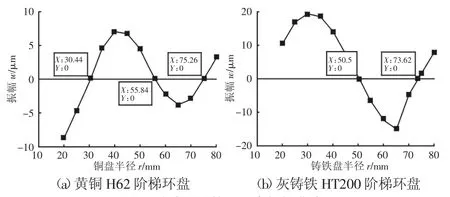
图5 试验测量的三环盘振幅曲线Fig.5 Amplitude Curves of 3-Annular Plate of Experimental Measurements

图6 三环盘端面振幅曲线对比Fig.6 Comparison of Amplitude Curve of Head Face of 3-Annular Plate
理论计算、有限元仿真和谐振试验之间的误差产生的因素可能有以下几点:
(1)试验时螺母对变幅器的刚度与质量具有影响,另外,螺母预紧力可能不足,从而产生误差;
(2)Matlab中对矩阵方程默认采用广义逆矩阵求解,因而会导致一定的求解误差;
(3)谐振试验时,测振幅直线不完全过圆心、测量点间隔不完全相等会影响测量精度;
(4)谐振试验中变幅器和试验台组成的整体发生谐振,从而产生误差。
5 结论
(1)基于Mindlin理论,建立了由变幅杆和阶梯环盘组成的纵弯谐振变幅器的频率方程,并求出了相应的三环盘振型解析表达,设计了大负载功率超声纵弯谐振变幅器。
(2)完成了纵弯谐振变幅器阻抗分析试验和谐振试验,变幅器的设计频率与阻抗分析结果和谐振试验结果相比最大误差为4.95%,理论计算与谐振试验得到的三环盘振幅曲线的整体形态基本一致,零振幅位置最大偏差为6.51%。
(3)为大负载功率超声纵弯谐振变幅器的应用奠定了理论基础,下一步将基于纵弯谐振变幅器设计旋转超声加工工具,为进一步开展大负载功率超声加工研究奠定实验基础。
