基于VC++的高等数学实验平台设计研究

程 飞

1 问题的提出

在实际教学中，开发具有交互功能、能表现三维动画、体现知识形成过程、适应特定教学环境、具有一定综合性的高等数学辅助教学平台能克服上述5类教学软件的不足，从而促进高职高等数学教学.限于篇幅，本文仅以高等数学教学体系中的“傅里叶分析（连续函数）”为例，予以具体说明基于VC++的高等数学辅助教学平台的开发过程.

2 傅里叶分析

周期为T的连续周期信号f(t)，可以展开为三角傅里叶级数［4-5］

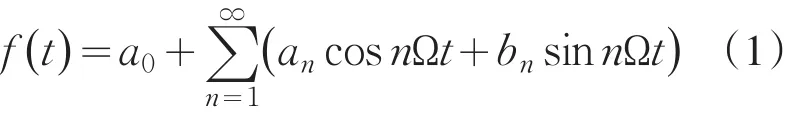
其中，

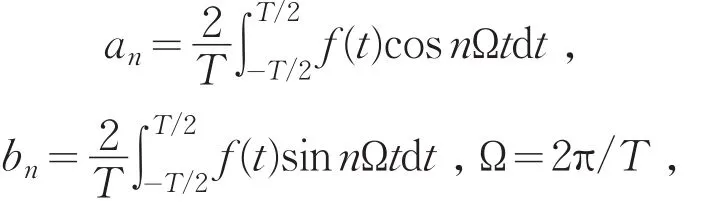
用指数形式表示为：

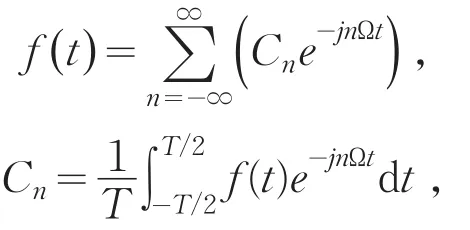
其中Cn为虚指数信号，| |Cn和频率的关系称为幅度频谱，一般采用双边频谱，则

（1）式中各个谐波的初相角与频率的关系称为相位频谱.

这一部分内容是进一步学习专业课程（如信号与系统、数字图像处理）的基础，教学地位十分重要.但是由于这一部分教学内容涉及到欧拉公式、时域频域转换，高职学生难以理解和接受.不仅如此，由于计算量大，各个谐波分量的系数an、bn不可能在有限的教学时间里采用直接计算方法得到.为解决这一问题，常规方法是采用MATLAB软件辅助教学.如图1和图2所示.该做法本质上仅起到降低计算量的效果，学生对于傅里叶分析的意义仍然没有具体的认识.而如果采用VC++技术，设计三维实验平台，就可以较好地实现教学目标.如图3所示.图3的左视图方向表现时域信号，而在主视图方向由近及远表现相位谱、频谱、谐波图像，在右视图方向表现各谐波的合成.

采用SPSS 21.0统计学软件对数据进行处理，计量资料以“±s”表示，组间比较采用单因素方差分析，多重比较采用LSD和Dunnet检验，以P＜0.05为差异有统计学意义。

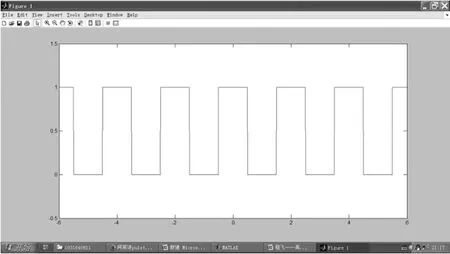
图1 阶跃函数

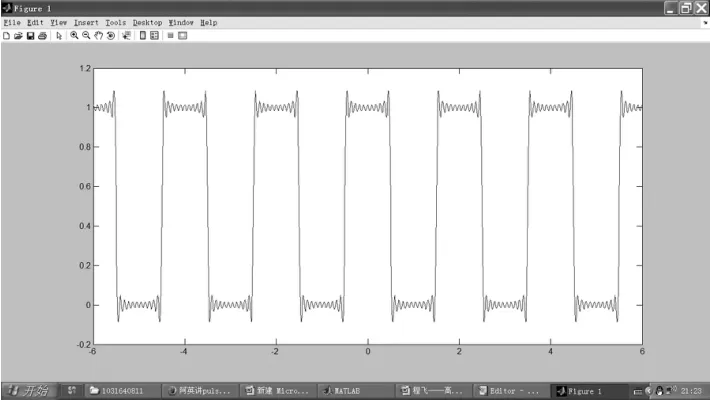
图2 n=21时傅里叶谐波的合成图像

图3 傅里叶分析实验平台（T=6，n=10）

3 实验平台设计

3.1 设计思路

在基于高等数学实验平台辅助教学过程中，学生需要通过自主操作实验平台，输入参数，获得并分析实验结果，获得关于数学原理的深刻认识.对于高职高等数学教学而言，数学知识的可视化、平坡化也必须考虑到.具体到本文所述傅里叶分析教学内容，平台应可实现：①学生通过输入参数n，可以获得各谐波的系数，并在三维坐标系中将谐波以图形的方式表达出来.如图3所示，阶跃函数分解为10次谐波，共有5次直流信号和5次交流信号（图中所示5条直线和5条正弦波）；②学生通过输入周期T的值，观察T值对于谐波图像的影响，如图4所示（此时T=2）；③观察不同T值和n值下的频域图像（连续函数的频域图像是离散的，如图3和图4所示）；④观察不同T值和n值下的相位谱（如图3和图4所示）；⑤合成图像的Gibbs效应［5］（级数的项数越多，合成波形的峰起越靠近不连续点，并从不连续点以起伏震荡的形式衰减下去），如图3和图4的右视图所示.

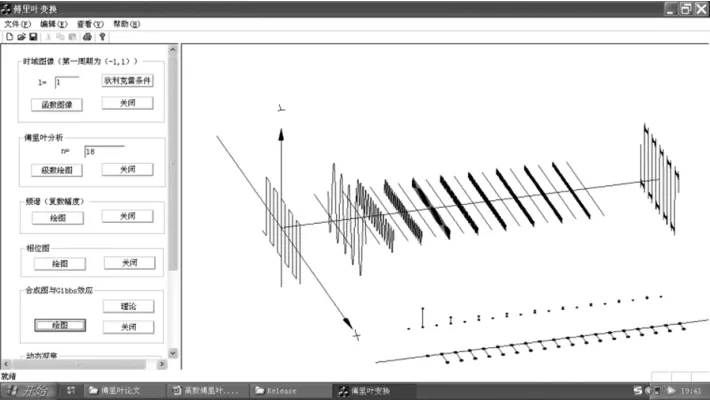
图4 傅里叶分析实验平台（T=2，n=18）

3.2 详细设计

（1）界面划分和按键控制.该平台输入值为T和n，而可视化输出包括时域图像、谐波图像、Gibbs效应、频谱、相位谱，因而界面划分为左右两个区.左边输入数据，包括多个功能组框，每个组框对应于上述的一个绘图功能，每个组框包括“绘图”与“关闭”两个按钮.每个组框的功能独立设计，互不影响.例如，时域图像绘制完成后，在“频谱”组框按下“绘图”按钮，则仅显示频谱图，如图5所示.再在“频谱”组框按下“关闭”键，关闭频谱图；在“相位谱”组框按下“绘图”按钮，则仅显示相位谱，如图6所示.这样可以使各个组框功能独立出来，便于根据教学需要显示不同的图形的组合.

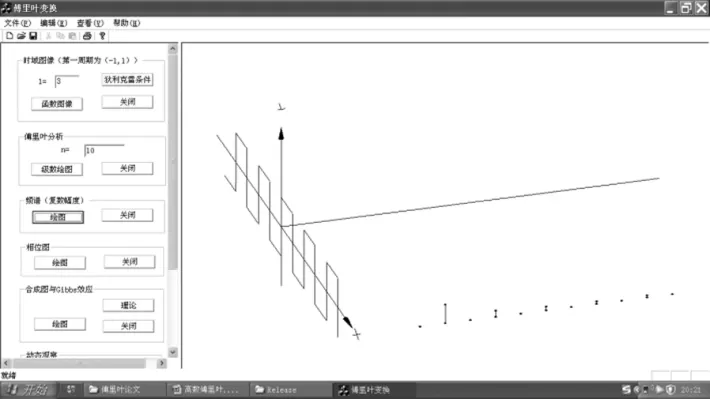
图5 时域图像和频谱（T=6，n=10）

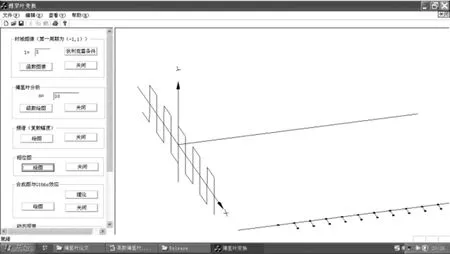
图6 时域图像和相位谱（T=6，n=10）

具体设计中，采用VC++的FormView-Doc-DrawView结构［1，6］，两个编辑框控件对应于输入的周期和谐波次数，在FormView、Doc、DrawView中对应的变量如表1所示.在Doc中对于变量首先赋值，软件启动初始化时，FormView和DrawView从Doc中取值，以FormView为例，代码为：按钮采用LHint机制，按钮按下将LHint值发送给所有的View，对应代码为：

这里LHint=1，在DrawView中对应于BOOL型变量flag1（绘图开关），LHint不同取值和各个flag对应关系如表1所示.

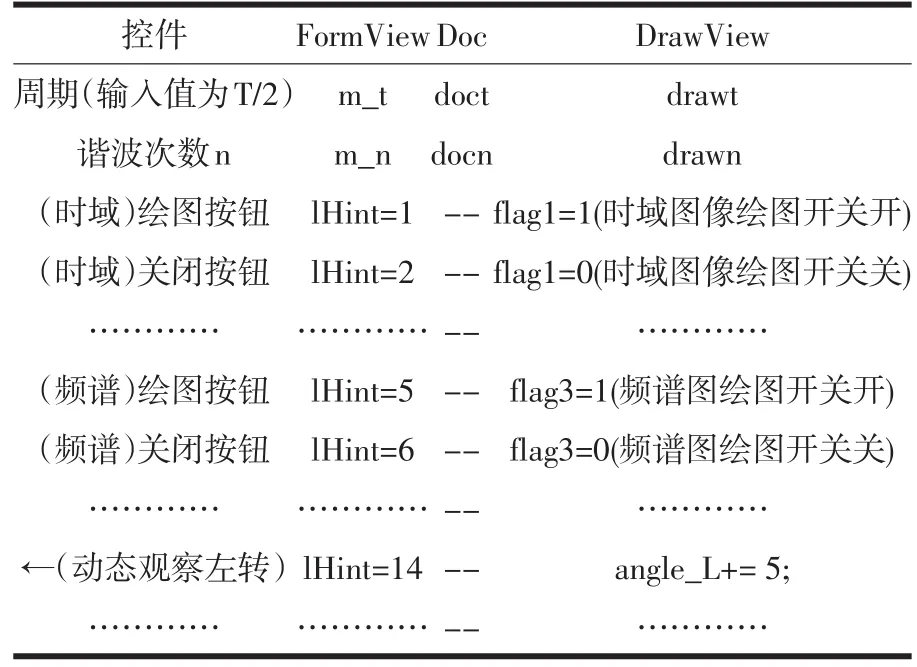
表1 变量对应表

（2）动态观察.对于该实验平台，当谐波次数增加的时候，仅从固定的角度观察会影响实验结果的分析，因而需要从不同角度观察，也采用LHint机制，以左转为例，代码如下：

视角函数为：

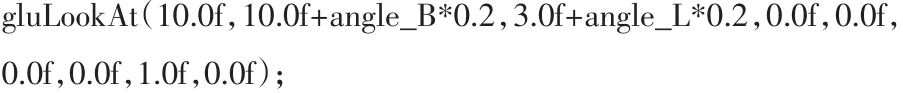
这里将三维坐标系中Y轴方向向上，以配合时域图像的绘制.绘制效果如图7和图8所示.

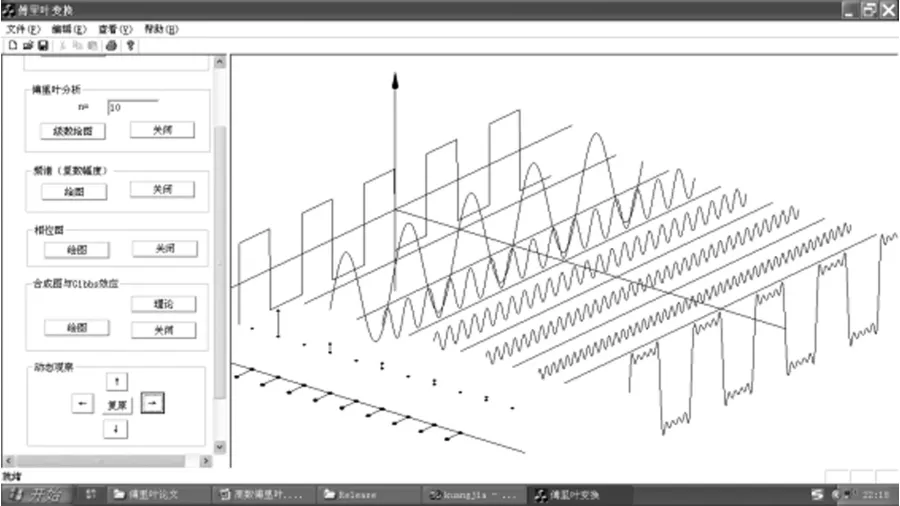
图7 改变视角的图像（右视图方向观察，T=6，n=10）

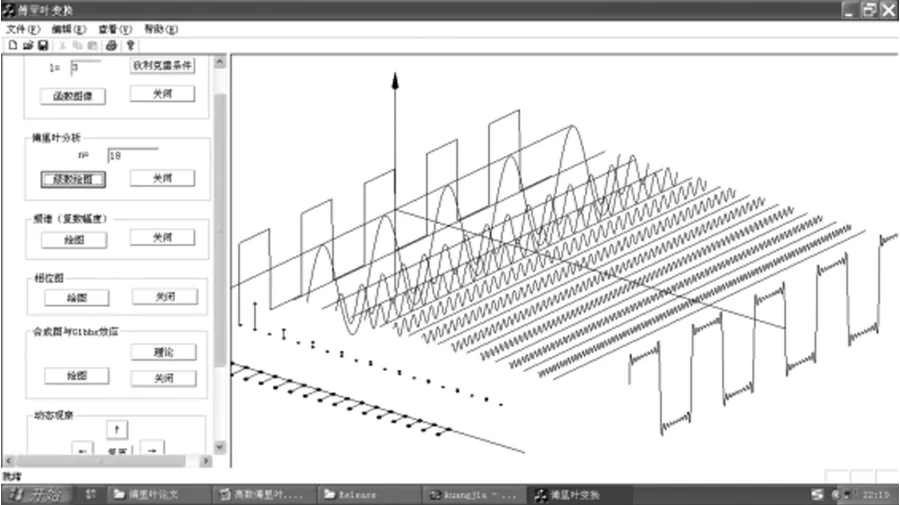
图8 改变视角的图像（右视图方向观察，T=6，n=18）

4 实验平台相关讨论

4.1 频域和相位谱分析

综合分析图5和图7，可以观察到对应于各频率，频谱对应的值为该频率谐波的振幅的1/2，即符合（2）式，由此可以进一步分析和深入研究双边频谱.而综合分析图6和图7，可以观察到对应于各频率，相位谱对应的值为该频率谐波的初相.

4.2 Gibbs效应

观察图7和图8的Gibbs效应图，可以快速理解和掌握Gibbs效应的规律，由图7（n=10）和图8（n=18）可见，图8的合成波形的峰起更加靠近不连续点.

5 推广

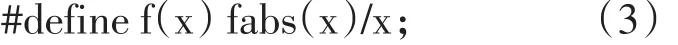
对于阶跃函数，首先定义然后计算函数曲线上各个点的坐标，代码如下：

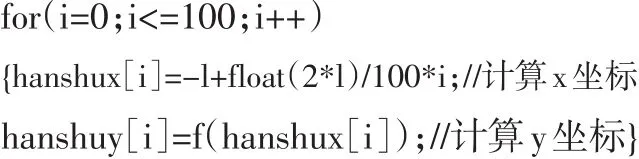
再使用OpenGL的glBegin（GL_LINES）命令绘图，得到函数曲线.首先得到的是一个周期的图像，其他周期图像可以通过平移定义域方式进行延拓.由于本实验平台是基于VC++的MFC开发的，如果设计其他函数的傅里叶分析实验，只要重新定义f(x)即可，计算坐标点的程序无需做改动.如果时域函数为线性函数，语句（3）修改为：

编译构建后软件效果如图9所示.

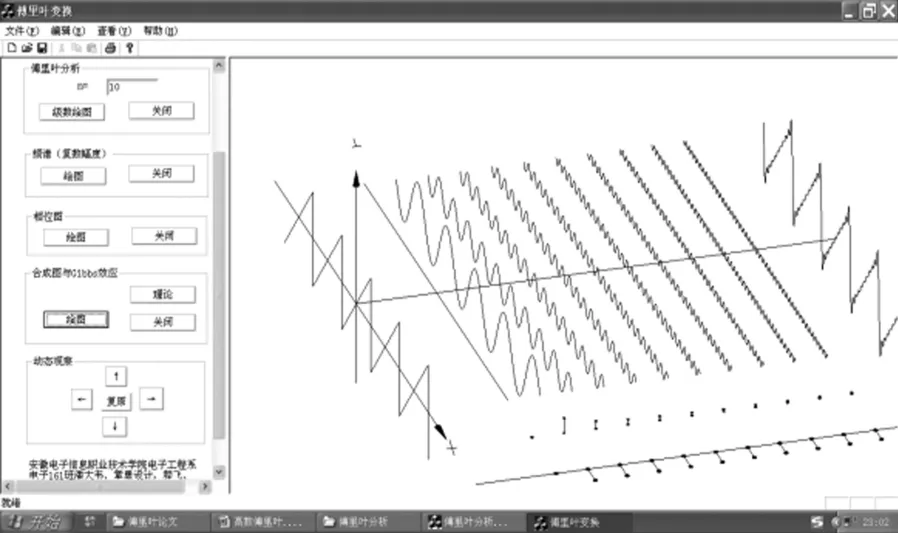
图9 线性函数傅里叶分析实验

如果时域函数为草帽函数，语句（3）修改为：

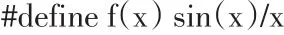
编译构建后软件效果如图10所示.

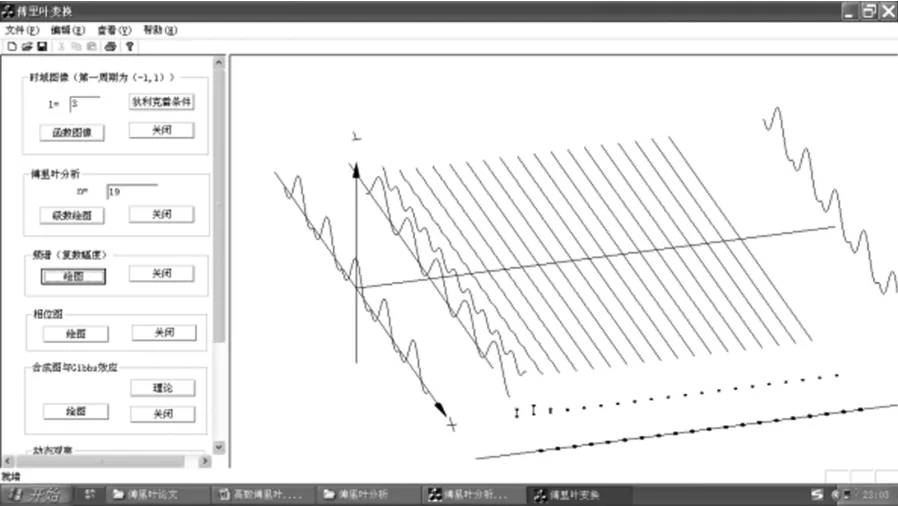
图10 草帽函数傅里叶分析实验

6 小结

高等数学实验平台的应用，可以将复杂深奥的高等数学知识可视化和三维化，进一步基于三维图形分析数学原理、各个表达式的数学意义，增加知识之间的关联，将高难度的数学知识平坡化，有助于复杂数学知识的理解和掌握.教学实践表明，基于该方法设计的数学实验平台易于开发设计，其使用可以明显提高教学效果，能有效克服MATLAB软件辅助教学平面化的缺点.学生通过参数输入，并对绘图结果进行分析和探究，开展数学学习活动.基于VC++开发的高等数学实验平台，有利于培养学生分析能力，促进学生数学思维的培养，是促进高等数学教学的有效手段.