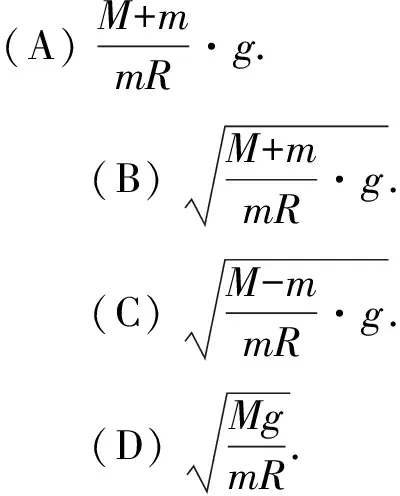剖析“竖直面内圆周运动”的两类错误命题
2018-07-18赵和平
赵和平
(浙江省象山中学,浙江 宁波 315700)
在高中物理教学中常将竖直面内的圆周运动问题归纳为“细绳模型”和“轻杆模型”.结合此类模型,能考查学生对机械能守恒定律、牛顿运动定律和抛体运动等相关知识的掌握情况,也能考查学生的建模能力、综合分析能力和应用数学解决物理问题的能力.在高考要求范围内只要求学生掌握对最高点和最低点受力情况的定量分析.这样在长此以往的针对训练中,师生难免形成思维定势,而没有系统的推导这类模型中力的变化规律,导致对此类问题把握不够全面和深刻,很容易出现一些科学性错误.笔者整理归纳后,发现在命制此类问题时易出现以下两种错误.
1 准确把握“轻杆模型”中杆对球作用力的变化规律,防范物体提早脱轨
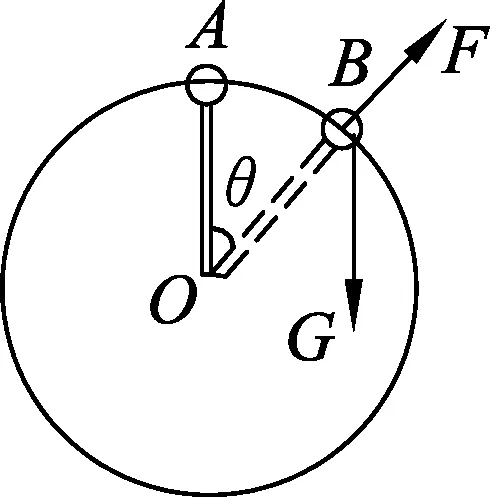
图1
理论分析:如图1所示,长为L的轻杆连着质量为m的球,杆连球在竖直平面内绕轴O自由转动.设在最高点处球的速度为v0,分析杆连球从最高处转过θ(其中0≤θ≤2π)时杆对球的力为F.
对杆连球从A到B,由机械能守恒定律得
(1)
假定杆对球的作用力背向圆心为正,在B处对小球受力分析有
(2)
由以上(1)、(2)式可得
(3)
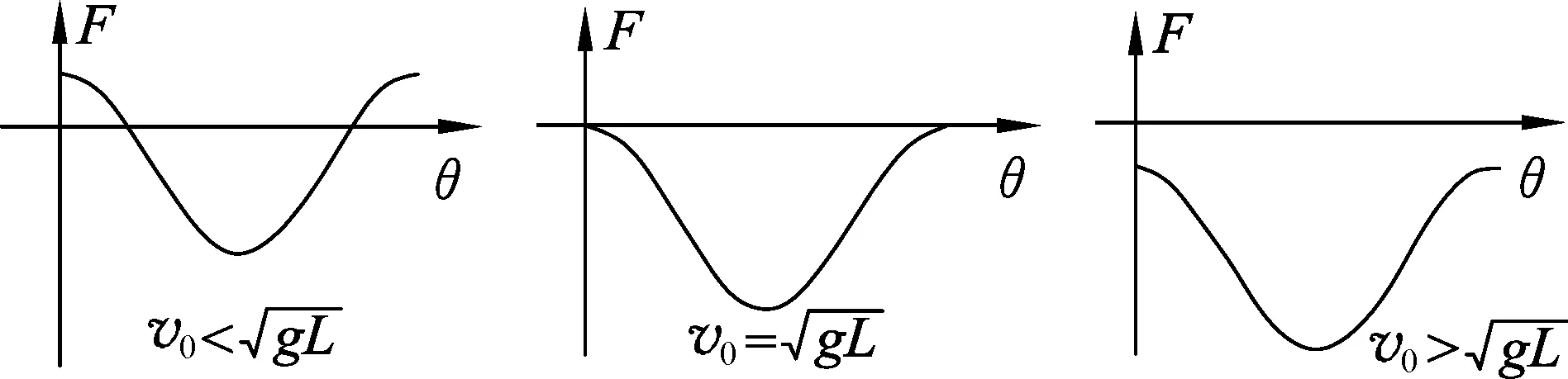
图2
讨论如下:

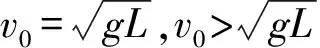
根据以上讨论,对于在竖直面内做圆周运动的问题中,仅有内侧轨道有约束的情景,在命制题目时,必须考虑“轻杆模型”中杆对球恰好没有作用力的位置,预防物体不能沿预设轨道运动而导致科学性错误.
错例1.(浙江省2017届高三稽阳联谊学校选考题第20题)某电视台拟推出一个水上娱乐节目,体验者乘坐滑水车运动过程可以简化为如下模型.如图3所示,滑水车从倾角为θ=53°的长直轨道AC上的B点由静止开始下滑,到达C点后进入弧形的涉水轨道CDEF,其中CDE是半径为R=5 m,圆心角为106°的圆弧,EF为半径为R=5 m,圆心角为53°的圆弧,此时滑水车刚好能到达F点.已知滑水车与体验者的总质量为60 kg,B点到C点的距离为L0=4 m,滑水车与轨道AC间存在摩擦,涉水轨道CDEF可视为光滑轨道,不计滑水车受到的其他阻力作用,则
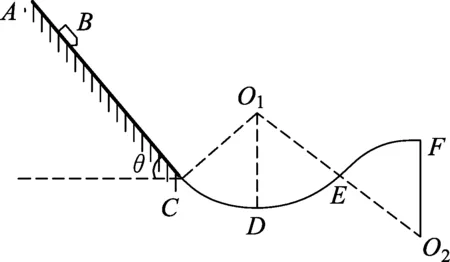
图3
(1) 求滑水车经过CDE轨道时对D点的压力;
(2) 求滑水车与轨道AC间的动摩擦因数μ;
(3) 若要使得滑水车能在F点水平抛出,求滑水车在AC上的释放点B′到C的距离L′的范围.
错误分析:该题要求水车刚好能到达F点,意味着到达F点时的速度为0,又设置了圆心角为53°>48.19°.这样水车根本不会听从命题者的命令,沿其设置的轨道运动到F点,更不会从F点水平抛出.笔者在教学过程中引导学生对该题进行修改,学生把圆心角改为30°,这样水车可能听从命题者的暗示,可以刚好到达F点,但第(3)问的解答就必须考虑的是小球在E点的速度不能过大,恰好到达E点时水车和轨道无作用力.这样修改虽然超出了浙江省的学考要求,但能很好地锻炼学生的思维能力,提升学生思维的深刻性.
2 准确掌握“轻杆模型”中杆对球作用力的竖直分力变化规律,防范轨道对地面压力最小未知的误判
理论分析:根据上面讨论中(3)式可得杆对球的作用力的竖直分力为
Fy=Fcosθ=
(4)
对(4)讨论如下:
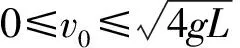

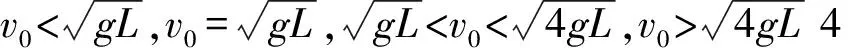
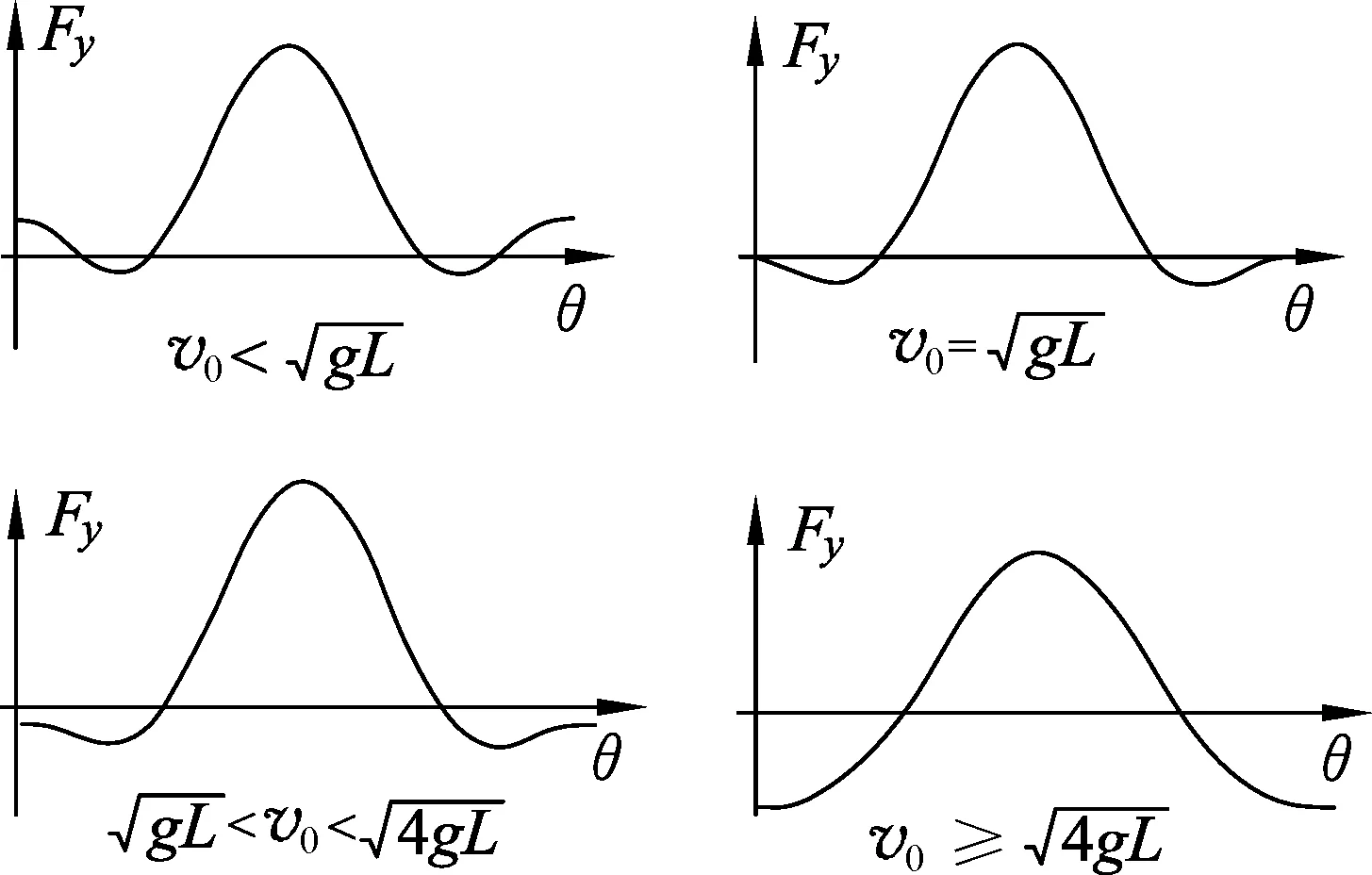
图4
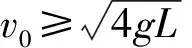
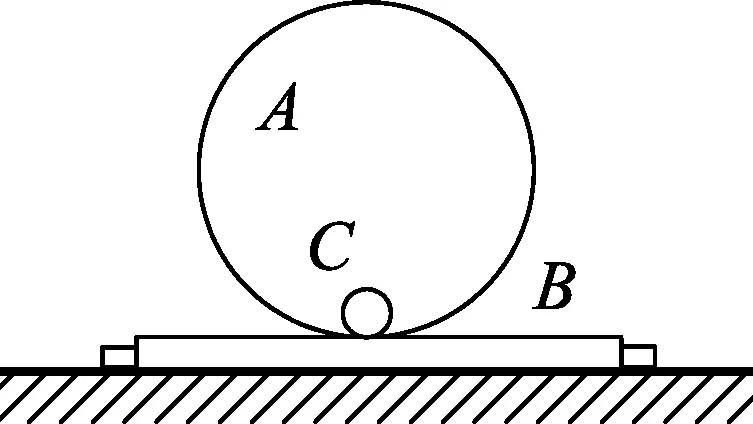
图5
错例2.(2012年豫南九校联考)如图5所示,竖直环A半径为r,固定在木板B上,木板B放在水平地面上,B的左右两侧各有一挡板固定在地上,B不能左右运动,在环的最低点静放有一小球C,A、B、C的质量均为m.现给小球一水平向右的瞬时速度v,小球会在环内侧做圆周运动,为保证小球能通过环的最高点,且不会使环在竖直方向上跳起(不计小球与环的摩擦阻力),瞬时速度必须满足
错例3.在质量为M的电动机飞轮上,固定着一个质量为m的重物,重物到轴的距离为R,如图6所示,为了使电动机不从地面上跳起,电动机飞轮转动的最大角速度不能超过

图6