信号处理教学案例：PCA正交变换教学案例

米吉提·阿不里米提，吾米提·尤努斯，艾斯卡尔·艾木都拉

（新疆大学信息科学与工程学院，乌鲁木齐 830046）

0 引言

PCA（Principle Component Analysis）是一个有效、应用广泛的信号转换方法。因为简单、无需多余的附加信息就能从复杂数据中抽取最重要的信息。PCA为降低维度、解开隐藏信息提供了捷径。较少数据冗余度，转换结果比转换前减少至少一个成分。能量集中在前部分。转换结果是个不相关的正交基，即是个正交线性变换。

PCA变换，在不同的应用场合有不同的名字，如Hotelling变换、KL变换POD变换、SVD变换等[1]。它是最简单的特征向量为基础的分析方法，他是通过方差分析数据的方法。由于能量集中在前部分，通过主要部分就可以代表整个多维数据，并达到很好的降维目的。但是，PCA和多个抽象概念领域有密切关系，因此需要简单案例来解释才能达到最佳教学效果[2]。

虽然有很多这方面的资料[3-4]，但是要么是过于抽象、难以理解并实现，要么就是概念模糊，所以本文以通俗易懂的方式讲解PCA变换。

1 理论及方法

我们的目的是找到一种变换Z=XW使得ZZT=I,最终使变换后的数据是个对角矩阵，这样变换后相关性就会消除。提取特征向量最好的办法是找出一个对称矩阵。Covariance协方差是很好的对称矩阵，它是正定矩阵，所以有正交特征向量，及实数特征值。

设X_由n个样本构成，每个样本的维数是p，则X_是n行p列,n*p,矩阵。设转换矩阵W是p*p方阵，X_归一化后的PCA变换是Z=XW。转换前及转换后的数据方差为：

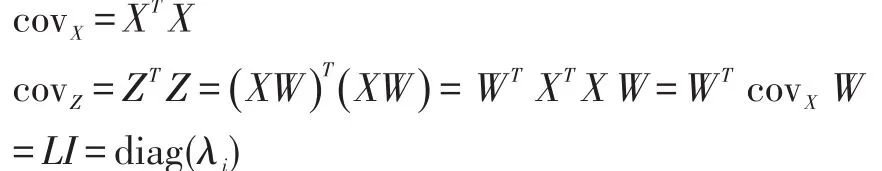
covZ,covX都是p*p方阵。covX是对称矩阵，covZ是对角矩阵，即消除了 covX的互相关性。特别需要说明的是，方差的计算方法covX=XTX需要先对样本X_进行归一化后才是正确的。归一化是指，从X_的每列减去该列的平均值。

即：

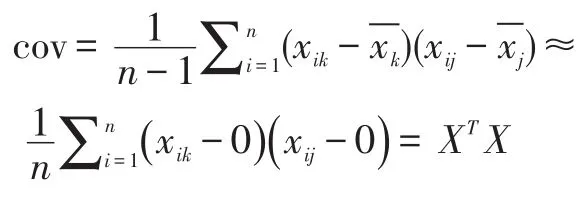
因为，协方差矩阵是个对称矩阵，它的特征向量之间是互相正交的[2]。这里需要些线性代数知识，尤其是特征向量（eigenvector）分解方法。简单特征向量求解方法如下：

A=cov则Avi=λivi其中λi是特征值,vi是对应的特征向量

VTA=VTLI=AV=LIV,其中，L是由特征值构成的一行[…λi…]

求解方法是：AV=LIV→det(A-LI=)0

V对应的特征向量集,每列一个向量vi

I是单位对角矩阵；V是正交集，对每个向量进行标准化，就变成了标准正交集（orthonormal），我们直接取W=V。标准正交矩阵有性质W-1=WT。

对于对称矩阵 covXW=WTcovX=LW

WTcovXW=LWW-1→WTcovXW=LI=diag(λi)

2 具体实例

简单PCA变换步骤是：

①对X_的标准化。

②covX特征向量的求解，并由大到小排序，排序依据是对应的特征值幅度的大小。

③转换矩阵W的构造。

④计算Z=XW。

假设有三个样本数据X_，对每列归一化变成X，然后计算 covX。

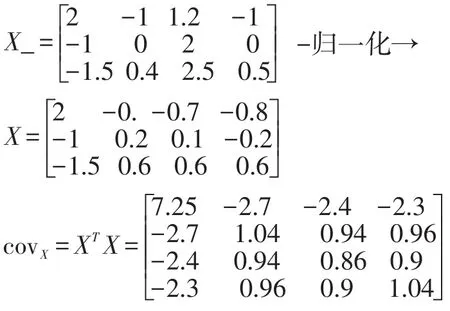
要计算特征值和特征向量，可以用行列式方法

大家可以用Python或MATLAB获得结果。也可以根据行列式的算法构成一个多项式函数，然后求解。

特 征 值L=[λ1λ2λ3λ4]=[9.8630.32400.003]对应的特征向量是：

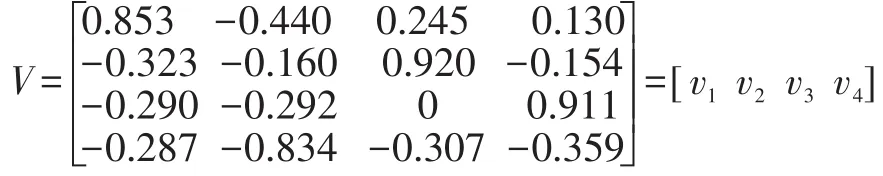
我们将特征值根据幅度从大到小排列L=[λ1λ2λ4λ3]=[9.8630.3240.0030]，对应的特征向量也要换位置。

然后计算PCA变换Z=XW

我们可以看到能量集中在前2列，我们将后2列设置成0，然后进行反变换。

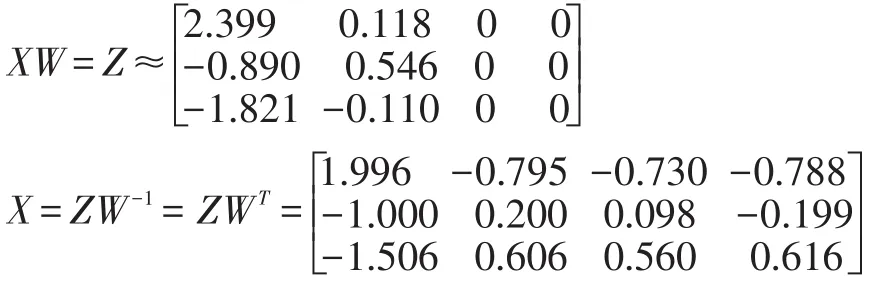
我们可以看到X的值比原始值变化很小。因此，通过小小的损失，将原来的样本的特征从4个减少到2个，有效消除了数据冗余。

3 结语

本文我们用简单概念讲解及实例来详细介绍了PCA转换的方法和步骤。虽然相关资料很多，但大部分资料要么概念形过于抽象，要么实例模糊。我门尽量用最简单的概念和典型的例子将概念和实践联系起来，为学生提供了教学案例。本文可能有不足之处，希望大家给予批评指正。