动态耐压下SOI RESURF器件的二维电场解析模型

雍明阳,阳小明,李天倩,韩 旭

(西华大学 电气与电子信息学院,四川 成都 610039)

SOI(silicon-on-insulator,绝缘衬底上的硅)材料因为具有高速、低功耗、可靠性高、抗辐射等优点,在低功耗电路、微机械传感器、光电集成等方面都具有重要应用[1-3]。而在实际电路运用中,由于SOI器件具有较高的开关频率,因此器件将承受快速变化的关断耐压,对此称其为器件的动态耐压。根据半导体物理学知识可知:在动态耐压条件下,衬底深耗尽效应将会出现从而导致耗尽区向衬底部分发展,改变器件的表面电场分布,对器件的耐压特性造成影响[4-7]。然而在现有的文献研究成果中,尚未就衬底耗尽区对表面电场分布的影响做出相关报道。所以建立相应的二维电场解析模型,分析动态耐压下器件RESURF效应变化的物理机制就显得尤为重要。

本文将建立动态耐压下SOI RESURF器件的二维电场解析模型,通过求解漂移区的二维泊松方程,获得新的表面电场分布表达式。阐述衬底耗尽区对器件RESURF效应的影响,从而为改善SOI器件在高频电路中的耐压水平提供依据。

1 漂移区模型建立

图1是衬底耗尽区宽度达到最大值瞬间,器件的横截面示意图。漂移区的掺杂浓度为NA,长度为Ld,漂移区厚度为ts,埋氧层的厚度为tox,衬底耗尽区的宽度为tx,漏极施加电压为VA。假设器件漂移区和衬底耗尽区已经完全耗尽,则漂移区、衬底耗尽区各点电势均满足二维Poisson方程,其中ϕ(x,0)为顶层硅表面电势,为衬底顶部表面电势:

利用泰勒展开式对方程进行线性化处理可得[8-10]:

将边界条件ϕ(0,0)=0,ϕ(Ld,0)=VA,式(5)代入式(3)求解可得式(6)。其中G(x,ξ)为格林函数,称其为特征厚度,Nx=为等效浓度。对比于静态耐压下表面电势的表达式[9],式(6)表明:动态耐压下,器件可等效看作静态耐压时漂移区为变掺杂的器件处理,其起始浓度为Nd。

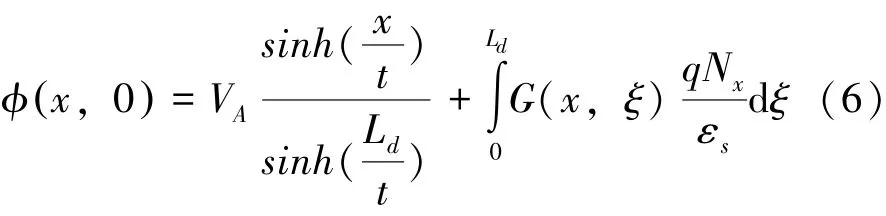
图1 动态耐压下SOI器件的横截面示意图Fig.1 Schematic cross section of SOI device under dynamic pressure

2 衬底耗尽区模型建立

式(4)跟一维电势的表达式一致,所以从本质上讲,衬底耗尽区只具有一维特性。因此,在衬底模型的建立过程中,本文将其简化为一维模型处理。由于衬底耗尽区与漂移区之间通过电场相互联系。因此衬底耗尽区的横向变化则由漂移区内横、纵电场的耦合效应来体现。同时,根据漂移区内电场耦合效应的不同,衬底耗尽区将被分为ADF、DFHK、HKJC三个区域进行分析。

2.1 ADF段衬底耗尽区模型建立

由于ADF段衬底耗尽区处于p+n结附近,其对应的漂移区内部纵向电场很小,电场基本由横向电场构成。由于横向电场的作用将会使得在p+n结交界面处靠左的位置形成ABE段衬底耗尽区。而它的横向耗尽宽度会随着衬底掺杂浓度的降低而增大。由于在现有的SOI器件研究成果中,并未涉及到对于ABE段耗尽区的研究。因此在建模过程中将对该区域进行分析。

因为在ABE段耗尽区内,横向电场很强,纵向电场基本为零。所以在ABE段衬底耗尽区的横向耗尽宽度可以看成一维耗尽宽度,即LAE。从E点开始沿着x的方向,横向电场会不断减小,纵向电场不断增加,且横向电场的减小量几乎等同于纵向电场的增加量。因此在ADF段耗尽区内,纵向耗尽宽度的变化率可以近似看作常数,而将耗尽边界由曲线等效成为直线。如图2所示。

在ADF段衬底耗尽区内,纵向电场会逐渐增大。在F点处,纵向电场等于一维纵向电场。采用电荷共享的方法来对ABD段衬底耗尽区域进行分析[11],从而可获得式(7)、(8)、(9):

根据电势等价原则,将ADF段衬底耗尽区转换成如图2所示的一维耗尽模型可得式(10):

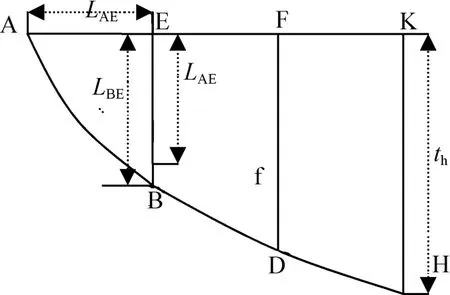
图2 ADF段一维等效示意图Fig.2 ADF one-dimensional equivalent schematic

2.2 DFKH段衬底耗尽区模型建立

受漂移区电场耦合效应变化的影响,在DFKH段衬底耗尽区内向会沿着x方向继续增大,超过一维纵向电场。在DFKH段衬底耗尽区内一维等效图如图3所示。其中th为H点处的纵向耗尽宽度,ϕK为K点表面电势ϕ(k,0),LKE为K点到E点的距离,。如图3所示:

其中ADF段与DFKH段两区域边界条件LEF为:

图3 DFKH段一维等效示意图Fig.3 DFKH one-dimensional equivalent schematic

2.3 KHJC段衬底耗尽区模型建立

在KHJC段漂移区内,对于横向耗尽区而言,起主要作用的是n+n结。而在常规的SOI器件结构中,其n+埋层非常薄(相比于漂移区厚度),因此n+n处的电场耦合效应基本上只限于器件表面处较薄的区域内。除此之外,为了获取较高的纵向耐压,SOI的埋氧层一般都比较厚。因此KHJC段漂移区内的横向电场对衬底耗尽区的影响很小,在KHJC段衬底耗尽区内基本上只有纵向电场作用,所以在KHJC段漂移区内ω(x,td)可按一维电势公式求解,该区域衬底耗尽区不需要再进行一维等效。其中耗尽宽度。由式(5)与一维电场表达式等价关系可得:

将式(10)、式(11)、式(15)代入式(5),再将其对x求偏导,整理可得新的表面电场:

其中,电势ϕE的值可以通过E3(x,0)和E2(x,0)在边界F点处的电场连续性得出。限于篇幅的原因,在此不再列出。E4(x,0)为ADF段衬底耗尽区对表面电场的影响表达式。

3 分析和讨论

文中所有的解析结果都将用二维数值仿真软件MEDICI进行验证。如图4所示为表面电场解析结果与仿真结果分布图,可见两者间具有较好的吻合,从而可以证明提出的模型正确性。对于常规的SOI器件而言,为使其能具有良好的耐压特性,在器件设计之初除衬底掺杂浓度以外的所有器件参数都已经被优化。因此在本节中,只讨论动态耐压下衬底掺杂浓度的变化对表面电场分布造成的影响。而不同的器件参数可以根据已给出的表达式,计算出相关表面电场的分布表达式,从而进行击穿特性分析。

器件的漂移区长度为Ld=25 μm,漂移区厚度为4 μm,漂移区掺杂浓度为Nd=2.5×1015cm-3, 埋氧层厚度为tox=2 μm。对于常规的SOI器件而言,随着外施偏压的提升,n+n结电场尖峰将迅速增大至临界击穿点,导致器件被击穿[10]。而根据E4(x,0)的表达式可知,在ADF段区域内,衬底耗尽区会对p+n结电场尖峰起增强作用。但是,当衬底掺杂浓度较高时,这种增强效应并不明显,p+n结电场尖峰并不会迅速达到临界击穿值。而根据E3(x,0)的表达式可知,越靠近n+n结处,衬底耗尽区对表面电场的抑制作用越明显,将以指数函数的形式迅速增强,并在n+n结处达到最大。因此衬底耗尽区的出现能够使器件不会被过早击穿,从而提升器件的动态耐压。由图4的仿真结果表明,当衬底掺杂浓度为NA=7×1014cm-3和NA=5×1014cm-3时,n+n结、p+n结的表面电场尖峰都低于硅的临界电场击穿值3×1015V/cm,而静态耐压时的电场尖峰值达到了3.8×1015V/cm,高于硅的临界电场击穿值。由此可以证明,衬底耗尽区的出现确实能够对表面电场尖峰起抑制作用。

衬底浓度越低,衬底耗尽宽度越宽,对n+n结电场尖峰抑制作用更加明显[6]。但是事实上,根据E4(x,0)表达式可知,当衬底掺杂浓度过低时,在靠近p+n结附近,衬底耗尽区对表面电场的增强效应迅速增大,导致p+n结电场尖峰过早达到临界击穿值,从而导致器件耐压水平降低。如图4所示,当衬底掺杂浓度为NA=3×1014cm-3时,p+n结电场尖峰迅速增加至临界击穿值,而n+n结电场尖峰非常低,整体耐压水平明显低于NA=5×1014cm-3时的情况。

图4 动态耐压下器件表面电场分布Fig.4 The surface electric field distribution of the device under thedynamic pressure

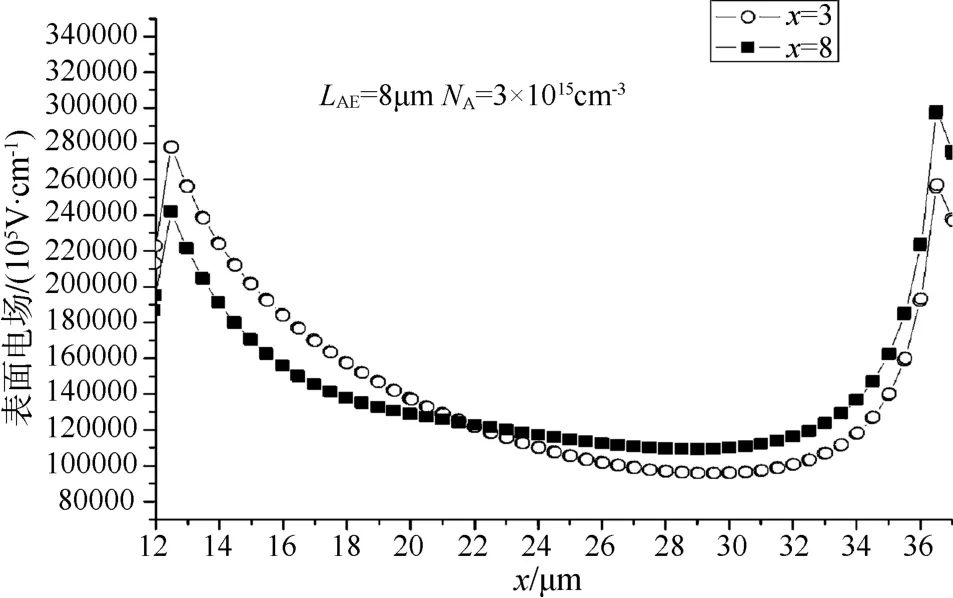
图5 衬底掺杂浓度优化范围对表面电场的影响Fig.5 Effect of substrate doping concentration optimization range on surface electric field

为了解决这一问题,提高p+n结附近衬底掺杂浓度的方法已经被提出[12]。但是在已有的文献中并未提及衬底掺杂浓度的优化宽度范围。而通过E4(x,0)表达式的计算,能够发现当E4(x,0)恰好为0时对应的x取值,为最佳边界取值。当x小于或大于此值时,对应的p+n结、n+n电场尖峰得不到较好抑制。图5为衬底掺杂浓度优化范围对表面电场的影响,当NA=3×1014cm-3时,x=3 μm取值偏小,p+n电场尖峰较高。x=8 μm取值偏大,n+n结电场尖峰较高。通过E4(x,0)的表达式能够准确地确定衬底掺杂浓度的优化范围,从而改善衬底低掺杂浓度对器件表面电场的影响。

4 结论

本文提出了动态耐压下SOI RESURF器件的二维电场解析模型,并推导出动态耐压下的表面电场分布表达式。获取的解析结果与仿真结果具有较好的吻合性。根据表面电场分布表达式,分析了动态耐压下器件的击穿特性,阐述了器件动态耐压提升的机制。此外,通过对p+n结附近衬底耗尽区的相关分析,找到了衬底掺杂浓度优化边界,从而为改善SOI器件在实际电路中的实用性提供相应的指导。