致密气藏水平井动态分析方法及生产规律
2018-07-17王德龙
杨 勇,周 文,王德龙
(1.油气藏地质及开发工程国家重点实验室(成都理工大学),成都 610059;2.中国石油长庆油田分公司 气田开发事业部,西安 710021;3.中国石油长庆油田分公司 勘探开发研究院,西安 710021)
致密气藏在开发过程中由于单井产量低、压力下降快、稳产期短或无稳产期等[1-2],使得致密气藏的生产动态分析面临着诸多的难题。国内外学者对此开展了许多研究,但在理论方面还未有重大突破[3]。目前,针对致密气藏动态分析,较多采用J.J.Arps[4]经验分析、M.J.Fetkovich[5-6]、T.A.Blasingame等[7]现代递减方法。
Arps递减分析方法是一种经验法,气井流动需进入边界控制流阶段,不同用于分析生产早期的不稳定流动阶段。M.J.Fetkovich通过联合不稳定曲线和Arps递减曲线,形成了Fetkovich-Arps递减曲线图版,但必须等到流动达到边界流后才能利用该图版。M.L.Fraim[8]引入标准化时间,认识到气井产量与标准化时间成指数递减关系,但应用有限。Blasingame建立流量积分函数、流量积分导数函数,但气井若未达边界控制流,气井动态分析偏差较大。之后,S.A.Cox等[9]、P.P.Valko[10]等学者研究气井渗流递减方法及规律。目前,各种气田分析方法均存在应用条件及优缺点,特别致密气藏水平井应用中存在很多显著问题[11]。
本文针对致密气藏水平井产量低、压力下降快,且常采用变流压生产[12-13]等特点,在Arps理论基础上,考虑了气体PVT物性变化和变流压生产,引入前人提出的拟压力标准化产量和物质平衡时间概念,提出一种水平井动态分析新方法,该方法适合变流压、变产量的气井生产的不同开发阶段。将该方法应用于苏里格气田致密气藏水平井的动态分析中,分析不同类型水平井渗流特征及递减规律,提高致密气藏开发效果。
1 致密气藏水平井动态分析方法
1.1 常规动态分析方法
Arps分析方法是最常用的动态分析方法[14]。在Arps模型中定义了递减指数n和递减率D。其定义分别为
(1)
(2)
其中:t为生产时间;q为气井日产气量;q0为初始产气量;D为递减率;D0为初始递减率。
Arps通过以上关系用来预测产量、累积产量、递减率等参数的变化规律[15]
q=q0(1+nD0t)-1/n
(3)
当递减指数n=0时,气井产量定义为指数递减;当n=1时,定义为调和递减;当n≠0且n≠1时,定义为双曲递减。
1.2 动态分析新方法
在实际致密气藏水平井生产过程中常采用变流压生产,压力变化大,因而气体的PVT物性变化大。为消除这些影响,本文提出了一套基于产量和压力耦合的动态分析新方法。该方法以Arps理论为基础,通过引入拟压力标准化产量和物质平衡时间的概念[16],对Arps分析方法进行改进。
拟压力标准化产量和物质平衡时间分别为
(4)
(5)
其中:μi为气体初始黏度;zi为气体初始压缩因子;pi为地层原始压力;q为气井日产气量;Cti、Ct(p)分别为初始时刻和压力为p时的综合压缩系数;Ψi、Ψwf分别为原始气体拟压力和井底拟压力,其表达式分别为
(6)
其中:p为气体实际压力;pi为地层原始压力;psc为标准状况压力(0.1 MPa);pwf为井底压力;μ(p)为压力为p时气体黏度;z(p)为压力p时气体压缩因子。
然后,将物质平衡时间和拟压力标准化产量分别代入式(3),可得
qs=qs0(1+nDs0ts)-1/n
(7)
其中:qs0为初始标准化气井产量;Ds0为初始标准化递减率。
对式(7)关于ts进行求导
(8)
定义拟压力标准化的产量递减率为
(9)
将式(7)和(8)分别代入式(9),化简可得
(10)
对式(10)求倒可得
(11)
最后,对式(11)关于ts求导,可得到拟压力标准化递减率与递减指数之间的关系
(12)
基于以上综合理论推导,建立一种新的综合考虑产量和压力的气藏水平井动态分析新方法。研究过程分为以下几个步骤:①考虑致密气藏水平井压力变化,采用(4)式对水平井产量进行标准化,计算出拟压力标准化产量。②基于气井累计产气量物质平衡原理,考虑气藏开发综合压缩系数、水平井产量、压力变化数据,采用(5)式对气井生产时间进行标准化,计算出物质平衡时间。③依据前两步计算的拟压力标准化产量和物质平衡时间参数,采用优化改进的Arps分析方法(9)式,得出拟压力标准化递减率,确定致密气藏水平井的产量递减规律。④依据拟压力标准化递减率,采用(12)式计算出拟压力标准化递减指数。⑤根据所计算出的拟压力标准化递减指数,划分致密气藏水平井的气体流动阶段,评价致密气藏水平井的递减规律。
2 水平井理论分析
本文依据苏里格典型区块储层地质及水平井开发参数:原始地层压力29.7 MPa、储层孔隙度8.5%,渗透率0.6×10-3μm2,水平井平均有效长度950 m、裂缝半长60 m等参数,采用Topaze生产动态分析软件,建立压裂水平井数值模型(图1),分析新方法描述水平井渗流阶段的曲线特征。依据新方法对建立变井底压力下致密气藏水平井的理论产量变化数据进行分析,可获得标准化递减率Ds、递减指数n与物质平衡时间ts的关系(图2、图3)。
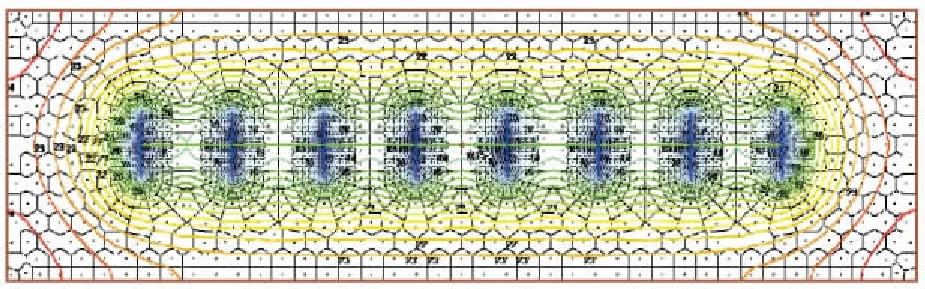
图1 压裂水平井数值模型Fig.1 Numerical simulation model for the fractured horizontal well
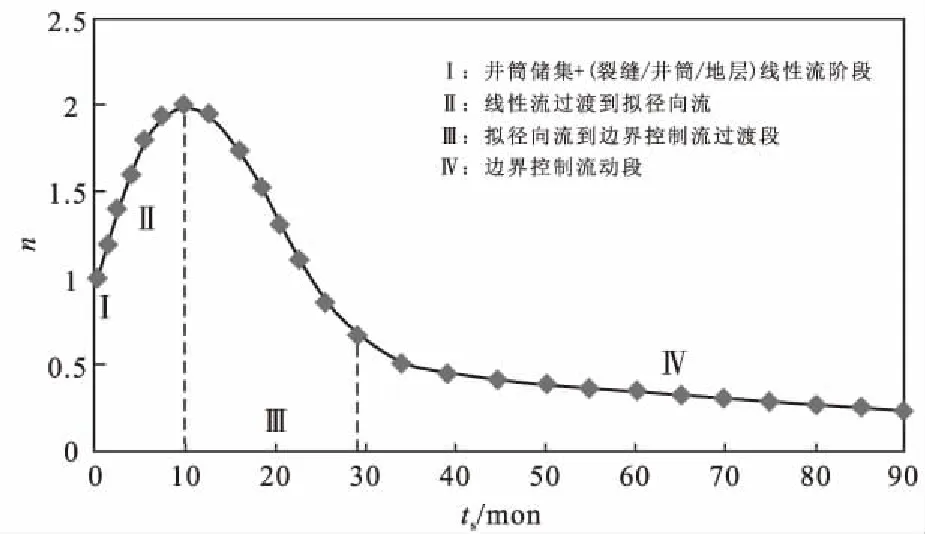
图3 理论模型拟压力标准化递减指数变化曲线Fig.3 Theory model for the variation curve of decline rate index of normalization pseudopressure
采用新的动态分析方法,绘制水平井理论模型拟压力标准化递减率与递减指数曲线。从图2可知:拟压力标准化递减率Ds的前期值迅速降低,后期值变化较小;标准化递减率Ds与物质平衡时间关系均服从幂指数分布。从图3可知:当水平井渗流未达到边界控制流时,标准化递减指数n与物质平衡时间ts服从抛物线关系;达到边界控制流后,二者存在线性关系。同时依据图3拟压力标准化递减指数曲线变化特征,对水平井流动阶段划分,具体分为4个阶段:①初始点Ⅰ点对应于井筒储集+(裂缝/井筒/地层)线性流阶段,其值一般大于1且小于2;②Ⅱ段表示渗流由线性流过渡到拟径向流,此段明显特征为递减指数由初始值上升到最大值2;③Ⅲ段对应于拟径向流到边界控制流过渡段,递减指数由2开始降低;④Ⅳ段则对应于边界控制流动段,其明显特征为递减指数为0.5或小于0.5。
通过理论分析认识到:相比常规递减分析方法,新方法充分考虑压力变化,形成拟压力标准化递减率Ds、递减指数n。二者不仅能描述水平井渗流过程中递减率变化特征,同时也能依据递减指数n变化特征,进一步判断水平井渗流阶段,准确实时反映水平井开发特征。
3 苏里格气田水平井生产规律分析
针对苏里格气田致密气藏实际生产的63口水平井,依据储层物性参数、水平井单位压降采气量、产量等参数将水平井分为3类(其中Ⅰ类水平井27口、Ⅱ类水平井21口、Ⅲ类水平井15口),对于不同类型水平井产量、压力数据进行时间拉齐均一化处理,采用新动态分析方法,研究苏里格气田不同类型水平井生产动态规律。
3.1 拟压力标准化递减率变化规律
针对苏里格水平井产量、生产时间进行标准化处理,并分别转化为拟压力标准化产量qs和物质平衡时间ts,获得拟压力标准化递减率Ds,绘制不同类型水平井Ds与ts的关系曲线(图4)。
从图4可以看出:Ⅰ、Ⅱ、Ⅲ类水平井的Ds初始值分别为0.011 d-1、0.015 d-1、0.018 d-1,Ⅰ、Ⅱ、Ⅲ类水平井拟压力标准化递减率Ds与物质平衡时间ts关系均服从幂指数分布趋势,与理论分析一致。Ds表现为早期快速下降,后期变化较平稳。在早期快速下降阶段,Ⅲ类井的递减率最大,Ⅰ类井的递减率最小;而在后期,Ⅰ类井的递减率最大,Ⅲ类井的递减率最小。具体幂指数公式为
(13)
从表1中可以看出:Ⅰ、Ⅱ、Ⅲ类水平井回归幂函数的系数A值逐渐增大、指数B值逐渐增大。相同物质平衡时间,Ⅰ类水平井拟压力标准化递减率Ds值较小,主要是因为Ⅰ类井的井控储层砂体钻遇率高,水平井段长,储层物性好,产气能力强,因此Ⅰ类水平井产气能力递减率较小。

表1 不同类型水平井递减率幂指数系数对比Table 1 Contrast of decline rate power coefficient for different horizontal wells
3.2 拟压力标准化递减指数变化规律
在拟压力标准化递减率Ds分析基础上,依据公式(12)获得标准化递减指数n,绘制不同类型水平井递减指数n与物质平衡时间ts的关系曲线(图5)。
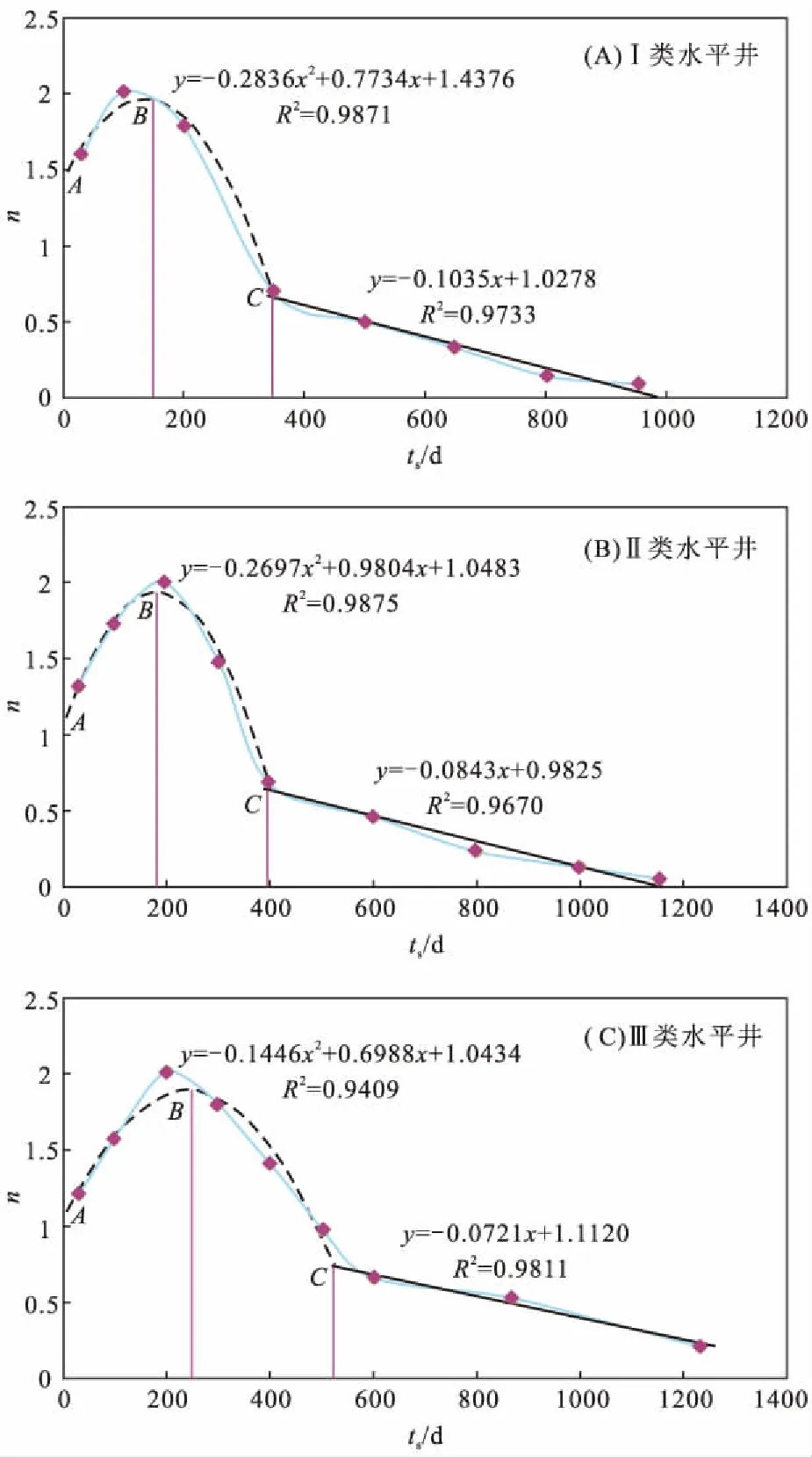
图5 水平井拟压力标准化递减指数变化曲线Fig.5 Decline index curve of normalization pseudopressure of horizontal wells
从图5中可以看出:Ⅰ、Ⅱ、Ⅲ类水平井的A点标准化递减指数初值(1.51、1.32、1.23)呈现逐渐下降趋势;递减指数从A点到B点表示由裂缝线性流过渡到地层拟径向流,Ⅰ、Ⅱ、Ⅲ类水平井分别平均需要146 d、180 d、230 d,水平井控制储层物性越差,达到地层拟径向流需要时间越长;递减指数从B点到C点表示由地层拟径向流过渡到边界控制流,Ⅰ、Ⅱ、Ⅲ类水平井分别平均需要350 d、400 d、520 d,此时递减指数分别为0.42、0.46、0.49。储层物性条件越差,水平井到达边界控制流动阶段所需时间越长。当水平井生产200~800 d天,Ⅰ类井递减指数下降幅度较大,Ⅲ类井下降幅度较小;800 d以后,Ⅰ类井递减指数下降幅度较小,Ⅲ类井下降幅度较大。
针对不同类型气井拟压力标准化递减指数与物质平衡时间曲线进行拟合,可以看出,Ⅰ、Ⅱ、Ⅲ类水平井的前3个渗流阶段(井筒储集+裂缝/井筒/地层线性流阶段;线性流过渡到拟径向流;拟径向流到边界控制流过渡段)的拟压力标准递减指数n与物质平衡时间ts服从抛物线关系
(14)
气井渗流到边界控制流动段后,n与ts服从线性关系
n=-βts+θ
(15)
不同类型水平井递减率指数与物质平衡时间关系式(14)、(15)的系数α、β如表2。
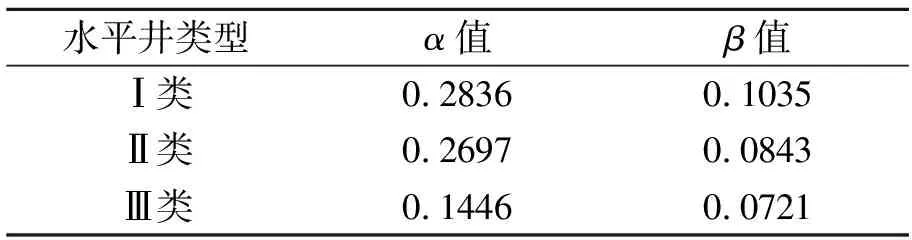
表2 不同类型水平井递减率指数与物质平衡时间系数对比Table 2 Contrast of decline rate coefficient power of different horizontal well
从表2可以看出:不同类型水平井拟压力标准化递减指数与物质平衡时间关系式的系数α、β值随Ⅰ、Ⅱ、Ⅲ类井逐步降低,说明水平井控制的储层越好,递减指数n随物质平衡时间ts变化幅度越大。
4 结 论
a.基于产量和拟压力相耦合的新方法,研究拟压力标准化产量与物质平衡时间关系,可以得出拟压力标准化递减率和递减指数,拟压力标准化递减指数与物质平衡时间关系呈现4个阶段。不同阶段,递减率、递减指数与物质平衡时间呈现不同变化特征。
b.应用所建立的新方法对苏里格气田典型水平井生产动态进行分析,分析结果表明Ⅰ、Ⅱ、Ⅲ类水平井标准化递减指数初值呈现逐渐下降趋势;Ⅰ类水平井天然气渗流能力强,达到地层拟径向流、边界控制流阶段所需要时间均较短,而Ⅲ类井所需要时间均较长;Ⅰ类井平均递减指数最小,但Ⅰ类井早期递减指数下降幅度较大,后期下降幅度较小。
c.分析3类水平井的平均递减率与物质平衡时间的关系:3类井的平均递减率均符合幂律变化规律,Ⅰ类水平井初期递减率较小,Ⅲ类水平井较大。Ⅰ、Ⅱ、Ⅲ类水平井回归幂函数的系数A值、指数B值均逐渐增大。
d.分析3类水平井的平均递减率指数n与物质平衡时间ts的关系:在水平井达到边界控制流之前,递减指数符合抛物线变化规律;在达到边界控制流之后,递减指数符合线性变化规律;相比较Ⅱ、Ⅲ类水平井,Ⅰ类水平井n随ts下降幅度较大。
e.采用新的方法,依据递减指数n变化特征,进一步可判断水平井渗流阶段,准确实时反映水平井动态产量变化规律。
