为生长而教，重构另一种可能——“分数初步认识（拓展）”教学尝试与思考

□　北京市中关村第一小学　董文彬

一、课前慎思

在准备“分数初步认识（拓展）”这节课之前，一件很有意思的事情激发了我的思考。

2017年6月，一次组内教研会，议题是“单元质量评价命题讨论”，内容是北师大版三年级下册“认识分数”单元。样卷中有这样一道题目：三年级学生已经初步完成了对分数意义的建构与认识：一个物体或图形作为整体的分数认识、一群（多个）物体或图形作为整体的分数认识，这里“整体”意义因得到拓展而内涵丰富；分数表示的是一个整体的一个部分，是整体与部分相互依存的数量关系；在用画图的方式表征一个分数的意义时，积累了由面积模型到集合模型的活动经验，包括操作的经验和思维的经验。

以上学习背景分析，激起了我一连串的疑问和思考：这样的题目真的“越界”、“超标”了吗？学生还没进一步延伸学习“分数的意义”和“分数乘法”就不能解决了吗？现有对分数的认知和经验能否帮助学生解决此类问题？如果真把这样的问题抛给学生，学生的接受度会如何？会有怎样的反馈与表现？三年级儿童对分数理解的生命力到底有多强？我想知道，我真的想知道。

第一，我思考教什么。

以这类题目作为学习素材依托，不可能延伸挖掘到五年级“分数其它意义内涵”，更不可能把“分数乘法”内容拿过来学，既不能“越界”，也不能“超标”。再思：分数的意义是分数运算的基础，分数运算是对分数意义的再认识。这节课可以不挖掘分数意义的其它维度如“比率”“商”“度量”和“运算”，但可以通过画图、运算表征问题，对分数“部分———整体”关系的意义作进一步的再认识，可以不教“分数乘法”运算，但可以在解决问题的过程中沟通分数与乘除法运算之间的联系，进而贯通分数问题与整数混合运算问题之间的联系。这节课能否让学生感受到这几个层面？我想尝试一下，我想重构另一种可能。

第二，我思考怎么教。

从情感态度来说，我希望学生亲近数学、喜欢数学、喜欢思考，因此我想让学生在本节课经历不断尝试、不断发现、不断质疑、不断收获的学习过程；从思维路径来说，我希望学生探讨的问题“由此及彼”、“层层剥茧”、“大道至简”、“由简驭繁”；从思想方法来说，我希望学生基于对分数核心概念的进一步再认识的同时，能够自主发现、构建和表达对数学必要的联系；从学习方式来说，我努力笃行在思维工具撬动、小组合作学习中，生生互动，分享交流，变“一言堂”为“群言堂”，在以“学”为中心的现场关注学生的实际获得，发现儿童数学生长的美好，让深度学习真正发生。

就这样，在不断审视与重建的思考中，“分数初步认识（拓展）”这节课已基本成型了！

二、课中践行

1、回顾旧知，唤醒经验

师：我们已经学习了分数，说说到目前为止你对分数已经有了哪些认识？

生：我知道分数是分东西“分”出来的，比如两个人一个苹果，平均每个人得到的就是这个苹果的一半，也就是。

生：我补充，为了公平，分的时候不能瞎分，一定要平均分，每份要分的一样多才行。

生：对，分数必须要“平均分”，分得“不平均”，不能用分数表示。

生：我知道分数各部分的名称，比如，这是分数线，4是分母，3是分子，读作四分之三。

师：那这个分数表示什么意思呢？解释解释。

生：就是把一个整体，比如说一块月饼，把它给平均分成4份，取其中的3份。4表示平均分的总份数，3表示取的份数。

师：嗯，整体在这里指分的是一块月饼、一个物体，还可以分———

生：很多块月饼、一群东西。

师：下面请自己写一个分数，并用你喜欢的方式表示出这个分数的意思。

（生在学习单上写、画。）

展示交流学生作品如下（略）。

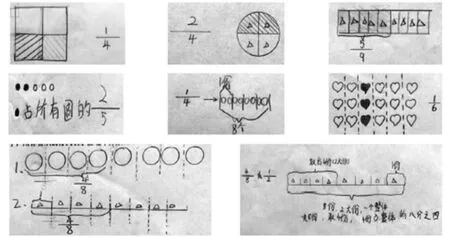
（注：有学生在图中标注“△”，是为表示分的每份一样多，这是我所教班级学生特有的图示“密码”。下同。）

【思考：通过回顾前期对分数的认识，特别是自主举例，用自己的方式表示分数的意思，唤醒学生已有的知识、思维经验，也为后面解决问题、探究发现积累图形表征的活动经验。需要说明的是，“平均分”一个单独图形或物体的学生还是占绝大多数，只有少数学生想到了“平均分”一个“群体”来表示分数意义，这是三年级学生的现实情况。既体现了本节课设计的重要价值，也说明了五年级再次认识分数时“平均分的对象主要是群体”的延伸的必要性。】

2、解决问题，融通生长

①初步感受。

出示“问题 1”：

师：已知哪些信息？要解决什么问题？

师：你觉得哪个信息特别关键？

师：这个信息怎么理解，这里的是什么意思？

生：这盒巧克力中有白色的，还有其它颜色，但白色占了这盒巧克力总块数。

生：就是把这盒巧克力6块看成一个整体，把它平均分成3份，其中的1份就是白巧克力。

师：不着急列式，请你先在学习单上画一画、分一分，画图描述问题表达清楚你的思考过程，再想想可以怎样列算式解决。

（生在学习单上画、分、写，师巡视指导。之后展示交流学生作品。）

陈企：我是这样想的（指下图），用小方形代表一块巧克力，一盒巧克力总共有6块，我就画出了6个小方形，这些小方形看成一个整体，先平均分成3份，每份是2个。白色巧克力占了一盒，也就是3份中的1份，1份是2块，那白巧克力就是2块。

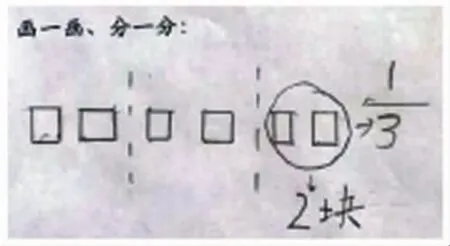
生：我同意你的想法，你的思路也很清晰，可是你没有列算式呀？

陈企：从图中就可以直接看出结果了，我圈出来的1份是2块就是白巧克力的块数，我就没列算式。

师：如果画图已经清晰地表达出了思考的过程和结果，完全可以不列算式。其实这里是有算式的，也有同学写出来了，谁来分享一下？

马敏程：我写的算式是6÷3＝2（块），画图后我发现其实我们要解决的问题就是把6块巧克力平均分成3份，求1份是多少，用除法计算。

生：同意，我也是这样写的算式。

师：列了算式的同学还有谁也是这样算的？

（全班45人有42名同学举手。）

师：我们再来分享几个典型的解答。

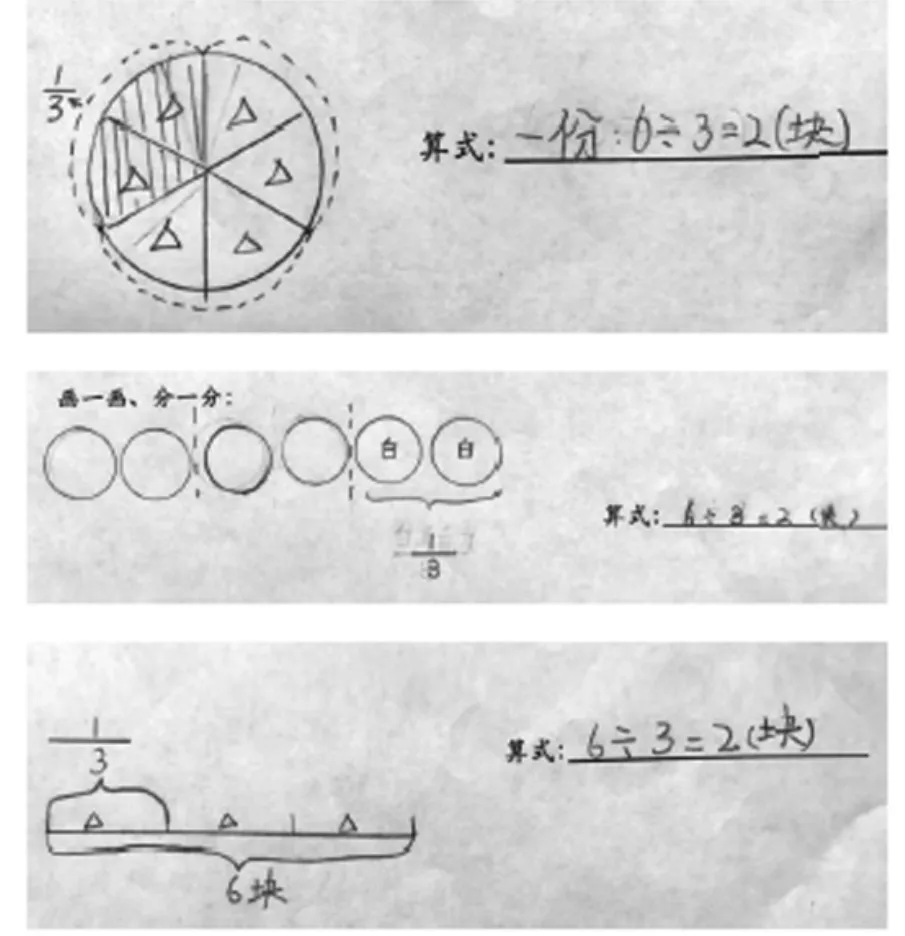
师：你能读懂吗？有什么感受？

郭简宁：他们画的图不一样，第一个是用一个大圆表示一盒巧克力，第2个是用6个小圆表示一盒巧克力，第3个是用一条线段表示1盒巧克力。

张明浩：虽然他们画的图不一样，但都表示出了这个分数，都是把一盒巧克力看成一个整体平均分成3份，求其中的1份是多少，都是用除法算式6÷3来解决。

师：真好！掌声送给以上同学！

【思考：从简单的分数问题开始，引导学生通过画图描述问题、表达思考过程，学生画图表征的过程，其实就是在进一步理解分数，是对分数意义的再认识。画图后用算式解决，是为了让学生初步感受在解决问题中分数与整数除法运算之间的联系。】

②拾级而上。

课件出示“问题2”：

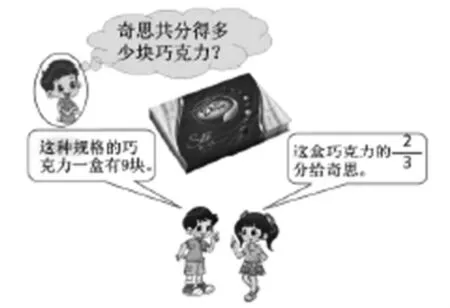
师：已知哪些信息？要解决什么问题？

生：巧克力换规格了，已知这种巧克力一盒有9块，要把这盒巧克力给奇思。求奇思能分得多少块巧克力。

生：就是把这盒巧克力9块看成一个整体，把它平均分成3份，其中的2份给奇思。

师：能解决吗？独立尝试一下。同样，先画图描述、分析问题的意思，把你的思考过程表示清楚。再想想可以怎样计算解决。

（生独立解决，师巡视指导。之后展示交流。）

王岳洲：我是这样想的，用一个三角代表一块巧克力，一盒有9块，我就画9个三角。然后把它们看成一个整体平均分成3份，每份就是这盒巧克力，奇思分，也就是分得其中的2份。要求2份是多少就要先算1份是多少，列式是9÷3＝3（块），再用1份乘2就是2份的块数，列式是2×3＝6（块），所以奇思共分得6块巧克力。

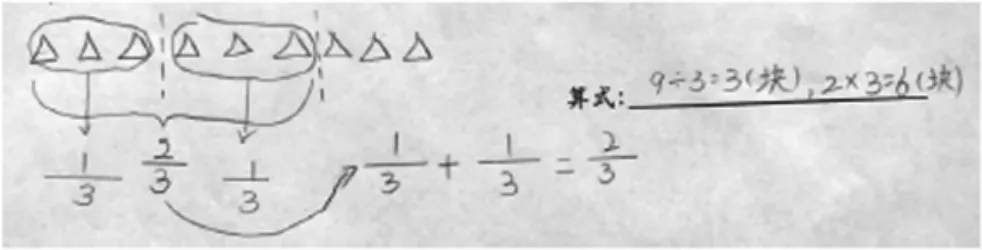
生：图画得很好，思路很清晰！

生：王岳洲是分步列式，我是用综合算式9÷3×2，最后结果也得6块。

生：我也列的综合算式2×（9÷3），计算完也是6块。

师：我们再来看几个同学的作品。

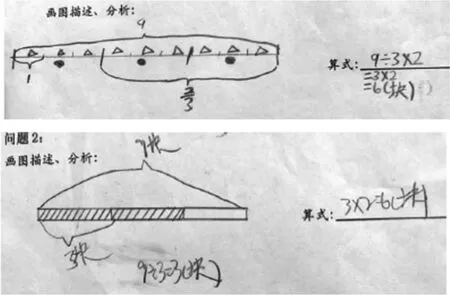
师：他们的解答怎么样？评价评价。

生：他们画的图不一样，但解答方法都是一样的。

生：列算式的思路也一样，都是先用除法算式9÷3算出1份是3块，再用乘法算式3×2求出2份是6块。

师：你们数学的眼光很敏锐！还有问题吗？

姚博元：我还有不同想法。

师：快和大家分享一下。

姚博元：（指下图）我同时画了2个图，和前面同学的意思都差不多。但我列出了两个综合算式，第一个也和刚才大家探讨的一样，但第二个我列的是9－9÷3，9÷3算的是1这盒巧克力3份里的1份是3块，通过画图能看出，奇思分走后还剩下，也就是说剩下的巧克力也占1份，所以只要用这盒巧克力的总块数减去剩下的1份就行了。

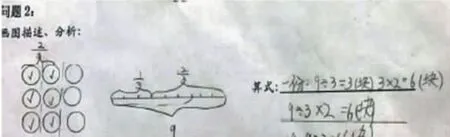
生（齐）：哦——

（教室里自发地响起掌声）

王雅祺：这个思路也很好。但我认为无论哪种方法关键都要先算出1份是多少才行。

生：有道理！

师：真是一针见血！再次把掌声也送给雅祺！

【思考：“问题2”比“问题1”要稍复杂一些，求的不再是“1份”，而是其中的“2份”，所以算式也要多一步。顺着思维的台阶拾级而上，让学生在解决问题中再次理解这个分数的意义，进而感受分数与除法、整数混合运算之间的联系，同时体会解决问题时思维路径的多样性。】

③层层深入。

师：接下来这个问题有点复杂，还敢挑战吗？

生（齐）：敢！

课件出示“问题3”：

师：说说信息、问题分别是什么？

生：奇思刚刚分到了6块巧克力，笑笑告诉他说，你分到的块数占现在这盒巧克力的。求现在这盒巧克力有多少块。

出示“学习建议”：

1、独立思考：画图描述、分析问题的意思，把你的思考过程表示清楚。再想想可以怎样计算解决。

3、小组分享：结合图与算式，说清楚你分析问题的思路、想法。

（生画图、思考、组内交流，师巡视指导，之后展示小组学习成果全班交流。）

展示王逸飞组成果（小组2人接力汇报）：

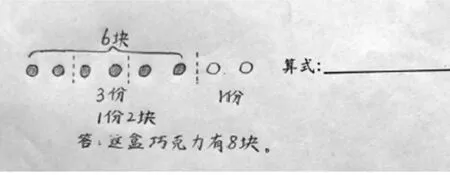
王逸飞：我们组的想法是这样的，我们用一个圆圈代表一块巧克力，奇思吃了6块，就先画出6个圆圈，涂上阴影表示吃的。奇思分到的占这盒巧克力的，意思就是把这盒巧克力平均分成4份，奇思分到了其中的3份，那就是说还剩1份。

陈一元：3份是6块，那1份就是2块。因为奇思分到了6块后还剩1份，只要在6个圆圈后面再画2个就行了，所以这盒巧克力一共有8块。

生：我明白了，你们的想法就是用奇思分到的6块加上剩下的，而剩下的正好是4份里的1份，也就是2块，就得出这盒巧克力的总块数了。

生：我觉得他们组图画得非常好，通过图就能一眼看出其中的一些关系了。

师：嗯，不错！通过画图描述、分析，一目了然！还有不同解决方法吗？

李宇涵：我们组是这样画的（指下图）。我们是用一个长条表示这盒巧克力，把它平均分成4份，其中这3份就是奇思分到的6块。我们要求的是整盒巧克力是多少，就是求图中的4份是多少。

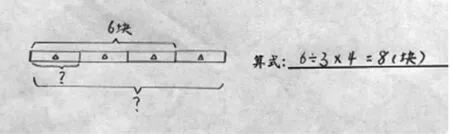
薛言渡：要求4份是多少，就得知道1份是多少，1份是6÷3，算4份再用1份的乘4，列算式就是6÷3×4＝8（块），这样就求出了这盒巧克力总共有8块。

生：你们组是把这盒巧克力分了之后，先求出1份是多少，再求4份也就是1盒是多少。

生：李宇涵她们与前面那个组，方法不同，但都得先求出1份是多少块。

生：其实不管王逸飞他们组还是李宇涵组，都画出了问题中“1份”的意思，通过他们画的图就能很清楚地看到淘气分到的、剩下的、和整盒巧克力之间的关系。

师：的确是这样。通过画图描述问题的意思，把分数按照理解画出来，再分析其中的数量关系，问题就迎刃而解了。为你们的分享和交流点赞！

【思考：“问题 3”比“问题 1”和“问题 2”还要稍复杂一些，是本次设计“问题链”的最顶端。相比前面的已知“整体”求“部分”，这个问题是已知“部分”求“整体”，思维路径不同，但解决问题的关键都是在理解分数意义的基础上先求“1份是多少”。同时多一个问题角度丰富对分数的再认识，并再次感受分数与除法、整数混合运算之间的联系。】

4、沟通关联，建立新知

师：刚才我们探究了有关分数的问题，回想一下解决这三个问题的过程，有没有共同之处？

生：都是画图分析的。

生：都要先明白问题中那个分数的意思，才能把图画对，也才能分析对。

生：我发现原来都是分数问题，可最后我们列出的算式都是整数的算式。

师：没错，其实今天我们探讨的分数问题的解决思路，其实以前就认识过。比如本学期第一单元就解决过类似的问题。

课件出示下图：

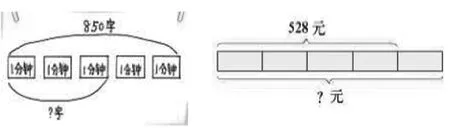
生（齐）：哦——

生：混合运算问题，以前学过。

生：都要先求1份是多少！

生：对，都要先用除法算出1份是多少，再用乘法算出几份是多少，这和我们这节课解决的后两个问题一样。

生：这节课解决的第一个问题其实也学过，就是简单的除法问题。

生：可是又不完全一样，以前学的是整数除法、混合运算，今天解决的是分数问题。

生：可是我们不是通过分析把分数问题变成了整数除法和混合运算吗？一样！

师：看来，我们今天探讨的分数问题和以前学过的除法问题、混合运算问题联系很大。想想为什么会有这样的联系？

生：我知道了，都是平均分东西！你看啊，平均分的问题就用除法解决，而分数也是平均分东西分出来的，都和平均分有关，分数的问题就可以变成除法运算问题了。

生：哦——有道理。

（教室里自发地响起掌声）

师：好棒！能找到知识方法之间的联系，是数学学习的最高境界！课虽然结束了，但我们对分数的认识、对问题的探索永无止境。

【思考：通过对解决问题学习过程的反思和回顾，让学生体会数学知识结构之间的关联：沟通新知与旧知之间的联系，分数问题与整数运算问题之间的联系，分数与除法之间的联系。以及为什么会有这样的联系，让学生知其然也知其所以然，最终对分数建立和形成新的认识。这是分数认识角度的另一种可能，在这个意义上我们能够看到学生的另一重数学生长。】

三、课后明辨

关于这节课，我确实考虑了很多。以至于在开始的研究中，我总想带着学生反思回顾，总结收获，拓展提升。现在的课上，我舍掉了。我舍得对吗？对，我的直觉告诉我对。课上到最后，已经不需要总结了，通过学生之间的生生互动、交流思辨就可以发现，学生在这堂课上收获了怎样的成果，那是一种深度的自然生长，一种别开生面的生长。学生对分数的认识重新打开了一个角度，分数与除法之间的联系，分数问题与除法运算问题之间的联系。我只是帮助学生学生提供了一座桥，课堂上实现了另一种可能，而这种可能是由学生建构的、创造的。

郑毓信教授说：“数学课中我们所希望看到的是学生能养成一种新的精神，它并非与生俱来，而是后天养成的理性精神。”而这种理性精神的培育主要来自于儿童在课堂中的数学生长，我们的数学教育应该为儿童的生长而教，生长会创造新的可能性，而构建数学联系又是数学认识、数学生长的核心一环。

审视———重建！

关联——重塑！

生长——可能！

我想，下节课，我有了笃行的新方向！