基于磁记忆和表面纹理特征融合的再制造毛坯疲劳损伤评估

刘　涛　鲍　宏　朱达荣　汪方斌　雷经发

1.安徽建筑大学机械与电气工程学院，合肥，230601 2.合肥工业大学工业培训中心，合肥，230601

0　引言

再制造过程中，由于再制造毛坯性能状态不确定，故导致制造成本和复杂程度大幅增加，这阻碍了再制造的产业化进程。针对再制造毛坯质量不确定的问题，已有多种无损检测方法被用来检测再制造毛坯表面/近表面的损伤［1］，但对于已服役一个或多个寿命周期的再制造构件，其损伤往往是复杂服役环境下多种诱导因素和结构功能特性耦合作用的结果，仅依靠单一检测手段难以实现损伤的精确定位和量化。为了提高评估可靠性，人们越来越多地利用多源信息（多特征量）在时间、空间上的冗余或互补，并依据某种准则来进行融合，进而获得被测对象的一致性描述，这已成为实现再制造毛坯损伤状态评估的有效途径。随着非接触式检测技术的发展，材料/构件的磁记忆特征和表面纹理特征被越来越多地应用到了损伤状态评估中。

对于铁磁构件，在外载荷（如循环载荷）作用下的结构损伤会导致材料磁畴畴壁位置和自发磁化方向的改变，反映为构件表面的宏观漏磁场变化［2］。人们常通过获取磁场强度值［3］，利用磁记忆信号法向分量过零点和切向分量存在极大值的特征曲线［4］，进行损伤的二维检测。此外，还有采用磁信号分量梯度［5］、表面三维自发漏磁信号［6］等方法识别应力集中，明确损伤与自发磁化漏磁场的量化关系［7］的方法。这种损伤演化过程会导致表面形貌的改变，如表面形成循环滑移带，沿滑移带剪切位移的不可逆使得材料表面变粗糙等，且这种粗糙表面会以微观峰（挤出）和谷（侵入）的形式显示出来［8］，并体现为表面粗糙度和纹理特征的变化［9］。人们通过对显微纹理图像进行变换［10］，提取粗糙度和波纹度形貌，分析了纹理特征参数与粗糙度的相关性［11］，逐步揭示了疲劳损伤过程连续点缺陷的迁移运动导致材料表面侵入和挤出的物理机制［12］。

磁记忆特征和表面纹理特征可以对铁磁金属构件的早期损伤、应力集中、疲劳裂纹萌生位置及其演化行为进行描述，两类特征在损伤评估中能够形成有效互补。将两类特征应用在工程中仍存在一些问题：描述疲劳损伤过程的磁记忆特征主要包括磁场强度法向、切向分量及其梯度，由于未考虑磁信号的时间序列复杂度，故在特征建模时可能会丢失部分损伤关联参数；在表面纹理特征提取时，形貌特征的复杂性导致对图像中纹理特征信息区分不明确，这些问题直接影响评估的精度及可靠性。

本文在进行特征建模时，基于疲劳损伤过程磁记忆特征变化规律，进一步提取了磁场强度及其梯度的样本熵值，结合时间序列复杂度建立损伤评估的磁记忆特征指标；在进行纹理特征提取时，选取灰度共生矩阵对纹理特征进行描述，得到沿不同方向的能量、熵、反差和相关4类典型参数。

1　磁记忆特征和表面纹理特征

磁记忆信号随疲劳损伤程度的不同呈现出规律性变化［4］，且磁场强度梯度和应力强度因子在疲

铁磁材料承受载荷时，因磁弹性和磁机械效应的联合作用，其内部磁畴会发生改变和重新分布，出现钉扎点，在表面形成漏磁场［4］，表现为应力集中部位漏磁场法向分量过零点，切向分量有最大值。工程中常选取法向磁场强度Hp（y）及其梯度值K作为探测目标进行信号采集。法向磁场强度梯度值K表征磁场强度的变化率。

利用pH（y）及其梯度值K，能够对应力集中部位进行初步判定，但由于磁化强度的变化不仅与应力有关，还与试样的初始磁状态有关，因此难以直接对零部件损伤状态进行评估。样本熵作为时间序列复杂度的一种度量，相对一致性较好，通过前期拉伸试验发现，样本熵能够明确反映损伤状态变化［14］，可用于进一步建立样本熵与损伤之间的量化关系。样本熵方法如下：

（1）已知原始数据r（1），r（2），…，r（N）。

（2）组成一组m维矢量：（Xm（1），Xm（2），…，Xm（N-m）），其中，Xm（i）=（r（i），r（i+1），…，r（i+m-1）），i=1，2，…，N-m。这些矢量代表从第i个点开始连续的m个r的值。

（3）定义矢量 Xm（i）和 Xm（j）间的距离 dij=max（|r（i+k）-r（j+k）|），其中，k=0，1，…，m-1;i，j=1，2，…，N-m，j≠i。

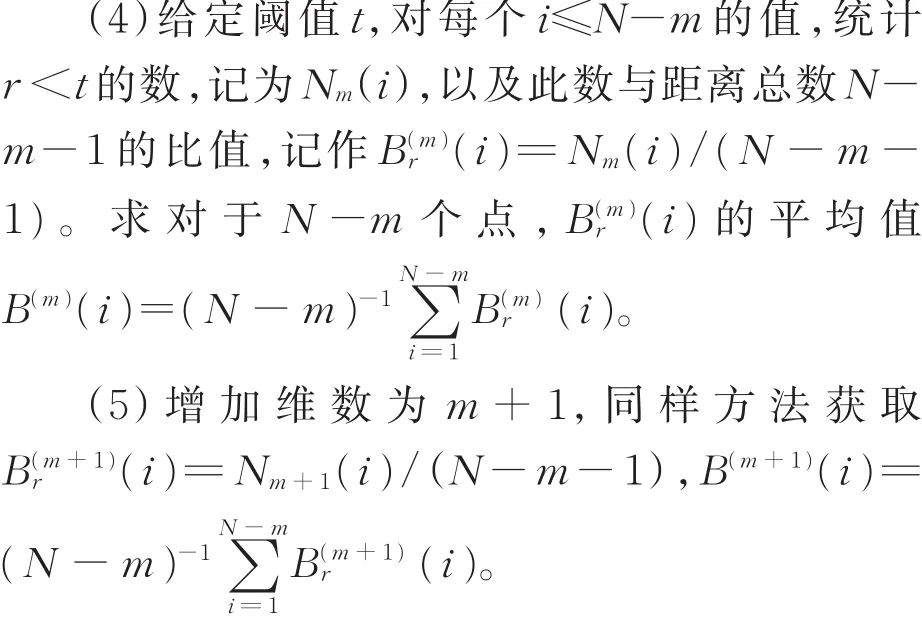
（6）定义样本熵值为-ln（B（m+1）（t）/B（m）（t））。

样本熵值与m、t的取值有关，m是选取的窗口长度，优先取2，t为各模式间的相似容限，即有效阈值，t一般在0.1δ到0.25δ之间选取（δ为数据标劳循环累积下均以指数形式增大，磁场强度梯度与疲劳裂纹长度之间、磁信号梯度与应力强度因子幅度（ΔK）之间亦存在一定程度的线性相关性［13］。表面纹理特征作为一种区域特征，能够较好地兼顾图像宏观性质与细微结构，可通过将疲劳损伤过程三维形貌变化特征映射在二维图像上，依据相邻像素点灰度等级差异，对表面形貌各像元之间的空间分布进行描述。

1.1　磁记忆特征建模

准偏差），能估计出比较有效的统计特性［15］。分别将各损伤阶段的Hp（y）和K作为原始数据，得到Hp（y）和K的样本熵。

1.2　表面纹理特征建模

鉴于灰度共生矩阵能够有效描述图像灰度在方向、变化幅度、相邻间隔等方面的信息，在纹理特征提取中应用广泛，选取灰度共生矩阵作为描述工具提取纹理特征，其原理如下。

设某个坐标（x，y）像素点的灰度为g（x，y），偏离它的另一点（x+a，y+b）的灰度为j（x，y）。若点（x，y）在整幅图像上移动，则会得到多种灰度g和j。设灰度值的级数为L，则g和j的组合共有L2种。统计每一对g和j出现的次数，再将其归一化为出现的概率 Pij，则称［Pij］L×L为灰度共生矩阵。距离差分值取不同数值组合，可得到某方向上的灰度共生矩阵。纹理特征不同，则体现出不同的方向特性，以灰度共生矩阵导出量，即能量、熵、反差和相关4种典型参数进行描述［16］。

（1）能量指灰度共生矩阵元素值的平方和，反映显微图像灰度分布均匀程度及纹理粗细度，表达式为

（2）熵指显微图像中具有的信息量的度量，表示图像纹理非均匀程度，表达式为

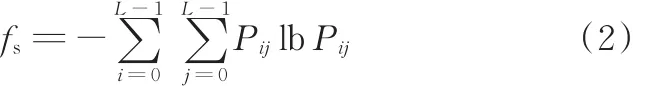
（3）反差指主对角线的惯性矩，数学表达式为

对于粗纹理，由于i-j数值在主对角线较为集中，i-j值较小，因此反差值小；反之细纹理相应的反差值大。

（4）相关指灰度共生矩阵元素在行或列方向上的相似程度，相关值大小反映了局部灰度相关性，数学表达式为

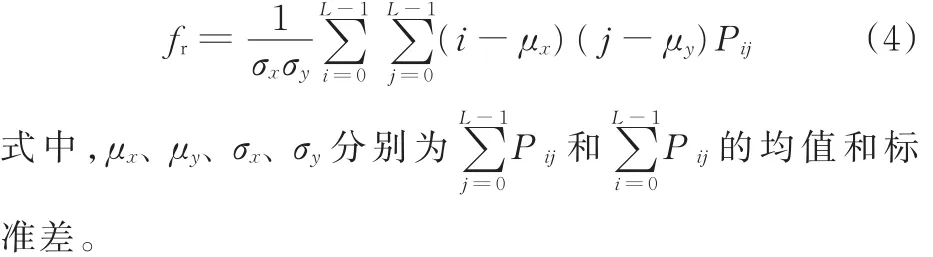
通过磁记忆和纹理特征建模，分别构造了4组磁记忆特征参数（-Hp（y）、K、Hp（y）和K的样本熵），以及4组纹理特征参数（能量、熵、反差和相关）。鉴于各特征参数与疲劳损伤状态之间的关系难以用公式直接表达，且人工神经网络具有学习、容错和高度的非线性映射能力，为减少冗余信息，提高评估精度，本文选取BP神经网络分别构造磁记忆特征参数子空间和纹理特征参数子空间到损伤状态空间的映射，分别用于磁记忆和纹理两类特征的数据层融合。

2　再制造毛坯损伤状态评估

2.1　评估流程

评估流程见图1。对于获取的再制造毛坯，首先进行清洁、外观检查和几何量公差测量。如果尺寸超差在允许范围内，则对其进行再制造检测，分别采集磁记忆信号和表面显微图，并按照第1节方法进行磁记忆特征和表面纹理特征指标建模。分别从数据层和指标层进行特征融合：在数据层，采用人工神经网络方法，分别将磁记忆特征量数据以及表面纹理特征量数据作为非线性映射的输入，建立其与损伤间的映射关系；在指标层，基于证据理论对数据层得到的磁记忆特征损伤映射和纹理特征损伤映射进行决策，以损伤状态为识别框架，基于基本概率分配函数（磁记忆、表面纹理特征的非线性输出），并采用Bayes近似，得到各证据信度函数值，最终实现损伤状态的融合评估。利用融合评估结果，可以对再制造毛坯损伤状态进行预判。

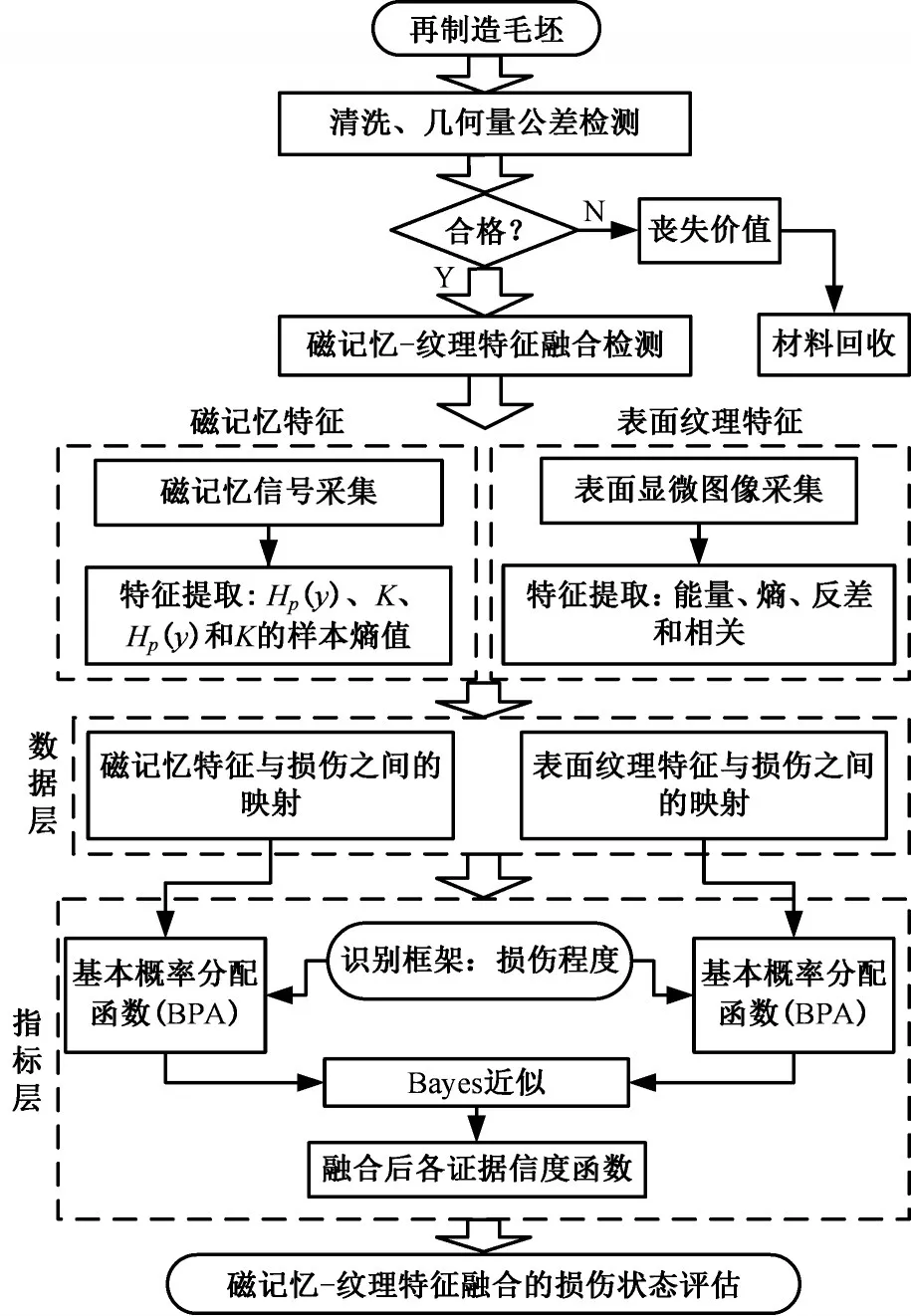
图1　损伤状态评估流程Fig.1　Damage state assessment process

2.2　磁记忆和纹理特征的数据层融合

鉴于BP神经网络可以实现从输入到输出的任意非线性映射，具有较强的泛化性能，选取BP神经网络分别用于两类特征的数据层融合。算法由两部分组成，即信息的正向传递与误差的反向传播。在训练BP网络时，需要先计算网络加权输入矢量以及网络输出和误差矢量，然后求误差平方和。当所训练矢量的误差平方和小于误差目标时，训练停止；否则在输出层计算误差变化，且采用反向传播学习规则来调整权值。重复此过程，最终以泛化方式给出输出结果。

（1）输入和输出层设计。输入层为磁记忆特征参数和纹理特征参数，以此两类参数分别构建神经网络。为了便于评估，引入损伤因子D对损伤进行量化，D为因疲劳损伤而丧失承载能力的面积与初始无损伤时的原面积之比，无损伤时D=0，完全破坏时D=1。设零部件破坏时循环加载总次数为q，等应力幅加载，取任一循环次数q0时，其损伤因子D0=q0/q，将损伤因子（0～1之间）作为网络的输出。

（2）隐含层设计。隐含层需要根据设计者的经验和多次试验来确定，且与具体问题、输入输出单元数目直接相关。可根据经验公式k+n+a确定隐含层数目，k为输入神经元数，n为输出层数，a为0～10之间的常数。

（3）训练、验证及测试样本。将加速寿命试验中得到的零部件损伤全过程磁记忆特征和表面纹理特征数据按比例随机抽取，作为训练样本、验证样本和测试样本。对样本进行归一化处理，将各参数数据标准化为［0，1］之间的数，进行网络训练、测试。

2.3　磁记忆和纹理特征的指标层融合

D-S证据理论是一个融合主观不确定性信息的有效手段，可以综合不同专家或数据源的知识或数据。

（1）基本概率分配（BPA）。定义Θ为一个识别框架，由5类损伤状态组成（零损伤、轻微损伤、中度损伤、重度损伤、破坏）。在识别框架Θ上的基本概率分配是一个2Θ∈[0,1]的函数m，称为mass函数，并且满足m（Ø）=0

m(A)=1，使得m（A）＞0的A称为焦元。

（2）信任函数及似然函数。信任函数也称信度函数，在识别框架上基于基本概率分配m的信任函数定义为

似然函数也称似然度函数，在识别框架上基于基本概率分配m的似然函数定义为

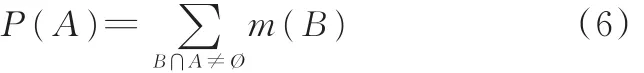
本文中，选取D-S证据理论进行磁和纹理特征的指标层融合，用信度函数表达概率大小，以数据层融合结果即磁记忆特征和纹理特征对应的不同损伤因子D为依据，进行基本概率分配。

如图2所示，损伤变量D取值范围为0～1，可根据损伤情况划分为5个区间，即0～0.2（零损伤）、0.2～0.4（轻微损伤）、0.4～0.6（中度损伤）、0.6～0.8（重度损伤）、0.8～1.0（破坏）。设数据层融合的拟合精度为P，且数据层融合后磁记忆特征和纹理特征输出分别为a、b，这表明通过数据层融合后，构件/试样损伤程度分别为a和b的可能性最大。由于正态分布是一种最为典型的中间型分布方案，被普遍应用于寿命预测，故可以通过正态分布模式，对损伤变量0～1区间的概率进行模糊指派，即以a和b为中心（均值），绘制概率密度图（正态分布），选取标准差s，使得（a-0.1，a+0.1）和（b-0.1，b+0.1）区间概率为P，并据此进行各区域的概率分配。

图2　特征指标的基本概率分配示意图Fig.2　Schematic diagram of the basic probability assignment of the feature indexes

（3）D-S合成规则。由于在损伤评估过程中，不存在既属于某一损伤状态又属于另一损伤状态的情况，因此，在D-S融合过程中，只需关心识别框架中的元素，而不用关心其子集的情况，这样可以减小计算量。利用Bayes近似计算公式，对上述基本概率分配分布进行重新调整，使评估结果更接近真实情况。根据基本概率分配的Bayes近似计算公式如下：

对于∀A⊆Θ，磁特征、纹理特征分别对应于识别框架Θ上的2个mass函数，设为m1和m2，合成规则为归一化常数

最终得到D-S理论融合结果，分别对应5类损伤程度的信度函数值，依据信度函数值对损伤程度进行综合评估。

3　应用示例

选取电液伺服疲劳试验机（200 kN）、EMS-2000+智能磁记忆诊断仪、图像采集系统，搭建磁表面纹理特征采集试验台。试验对象为Q235试样，由激光切割加工，并沿轴向打磨抛光，试件的尺寸见图3。经X射线荧光光谱分析，得到材料化学成分（质量分数）如下：w（C）=0.220%，w（Mn）=0.650%，w（Si）=0.230%，w（S）=0.045%，w（P）=0.040%，w（Cr）=0.044%，w（Co）=0.081%，其他为Fe。拉伸试验获得材料的屈服强度为300 MPa、抗拉强度为415 MPa，材料未经专门磁化和退磁。

图3　Q235材料试样Fig.3　Q235 specimen

3.1　数据采集及处理

在室温下开展轴向拉伸疲劳试验，选取12组试样，采用恒定应力幅值，正弦波，加载频率为10 Hz，载荷均值为23.1 kN，峰谷值为18.9 kN。沿试样纵向中心线，从左至右进行磁信号探测，探测距离为40 mm，且以试样中心点为对称点，分别采集疲劳循环加载次数Q为1 000、2 000、4 000、6 000、8 000时的磁记忆信号及其梯度值，并进一步提取其样本熵值；以试样中心点为对称点，采集10 mm×10 mm区域（图3中A）表面显微图像，并提取其纹理特征（能量、熵、反差和相关），部分疲劳损伤阶段的表面显微图见图4。

3.2　磁记忆　表面纹理特征融合评估

采用反向传播算法的BP神经网络进行磁记忆特征和表面纹理特征的数据层融合，建立其与损伤之间的非线性映射。输入节点数、隐层节点数、输出节点数、训练目标、训练次数分别为3、10、1、1×10-5和2 000。图5、图6分别为采集的磁记忆特征（法向磁场强度及其梯度值）及纹理特征（能量、熵、反差和相关4类参数）趋势图。

图4　各疲劳阶段试样显微图Fig.4　Micro-images of each fatigue stage

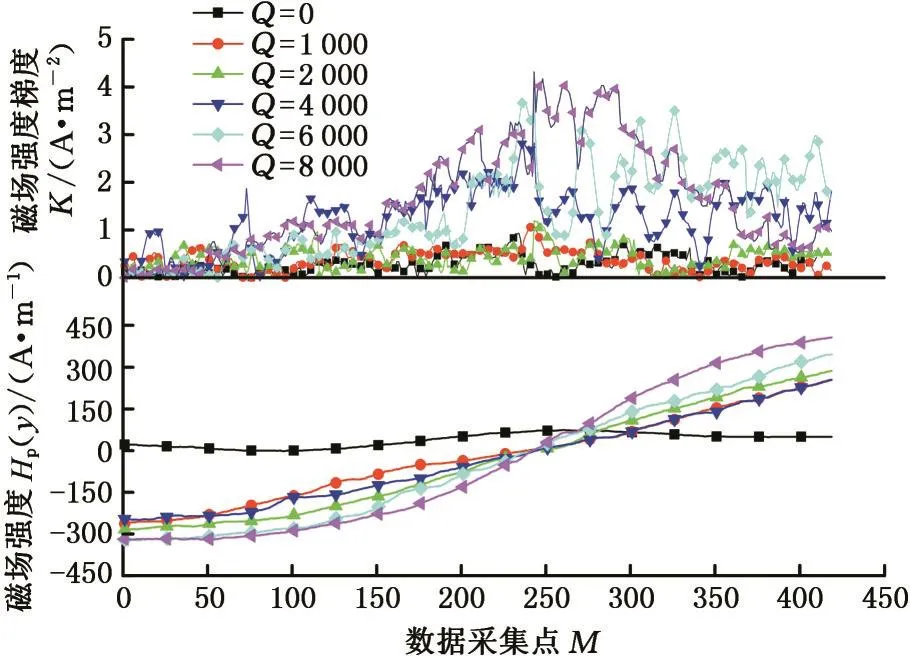
图5　法向磁场强度及其梯度Fig.5　Normal magnetic field intensity and its gradient of one specimen

图5中横坐标为对应于探测路径的数据采集点，可见，在疲劳损伤过程中，不同循环载荷下试样表面法向磁场强度曲线均存在零值点。随着损伤程度的增加，磁信号强度也相应增大。从各损伤阶段法向磁场强度梯度曲线可以看出，最高峰值位置与过零点位置相近，随着损伤程度的增加，各阶段最高梯度值也相应增大。

图6中取值为各组试样的特征均值及方差，可见，能量和相关参数值随着损伤程度的增加而减小，熵和反差参数随着损伤程度的增加而增大。

尽管各试样的材料、尺寸和试验方法一致，但仍存在一定的数值差异。对于磁记忆特征，每个试样提取6组数据，即对应于6类损伤状态（循环周次）的磁信号均值、磁信号梯度峰值、磁信号样本熵值和梯度样本熵值。对于表面纹理特征，提取损伤过程中每个试样的9组显微图像。对于12组试样，共获取磁记忆特征数据72组，表面纹理特征数据108组。从样本中随机选取70%的数据作为训练数据，15%的数据作为验证数据，15%的数据作为测试数据。网络的隐含层神经元传递函数为tansig，输出层神经元的传递函数为purelin，网络的训练函数为trainlm（对应Levenberg-Marquardt算法），对网络性能进行测度，得到拟合精度分别为91.86和95.80。

损伤状态预测：另取5组预测试样（材料与加工方式与上文中保持一致），通过疲劳试验对其进行损伤预制，其损伤程度（疲劳循环周次Q）分别为2 500、3 000、3 500、4 000、4 500，对应的实际损伤（以损伤因子D表示）分别为0.305、0.366、0.427、0.488、0.549。采集各试样表面磁信号及显微图像，并进行磁记忆特征和纹理特征提取。以试样3（Q=3 500）为例，采集得到的磁记忆特征及纹理特征值为（-58.392 8，2.720 1，0.016 0，0.619 9）和（0.201 0，0.077 5，0.758 3，3.013 3），通过数据层预测，得到输出为0.515 4、0.381 1。以0.515 4和0.381 1为中心（均值），选取标准差0.057 5和0.049，绘制对应于概率密度的预测频率图（图7），对损伤变量0～1区间的概率进行模糊指派，分别用D1、D2、D3、D4、D5代表5类损伤状态（零损伤、轻微损伤、中度损伤、重度损伤、破坏），为了提高最终的指标层融合精度，在两相邻损伤阶段之间设置边界，当试样损伤程度处于两损伤状态间的临界状态时，利用边界进行概率分配。用于界定边界的损伤因子取值范围可以根据具体情况进行划定，本例中边界划分及概率分配结果见表1。

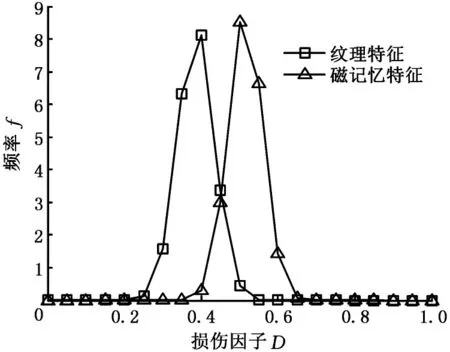
图7　损伤状态预测频率直方图Fig.7　Predictive frequency histogram of damage state

表1　模糊概率分配结果Tab.1　Fuzzy probability distribution results

采用Bayes近似计算方法对上述基本概率分配分布进行重新调整，得到调整后的概率分配及其D-S计算结果，见表2。

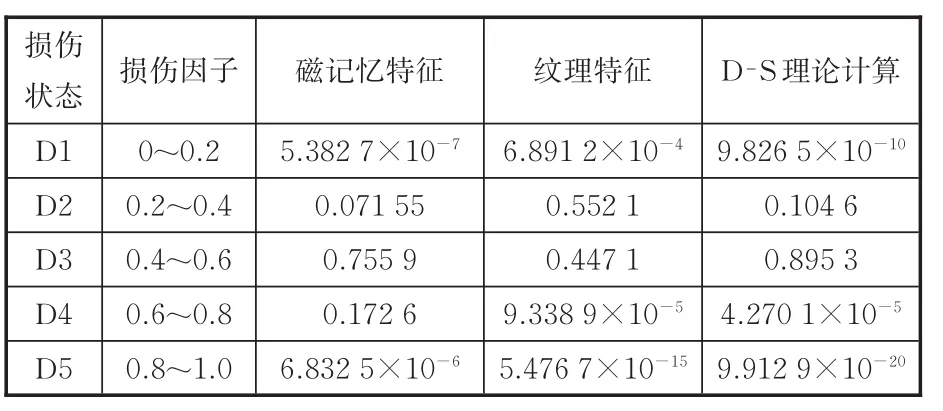
表2　D-S指标层融合结果Tab.2　D-Sindex layer fusion results

通过数据层和指标层融合，并参照表2评估结果，得到试样损伤阶段位于D3（即0.4～0.6，中度损伤）的可能性达到89.53%。同理可以得到另外4个试样的预测结果，对比预测结果与实际损伤变量值，可见预测结果与实际相吻合。

4　结论

本文提出基于磁记忆和纹理特征融合的再制造毛坯损伤评估方法。结合磁信号的时间序列复杂度，建立损伤评估的磁特征指标（法向磁场强度Hp（y）、梯度K、Hp（y）的样本熵以及K的样本熵），并选取灰度共生矩阵描述表面显微图的纹理特征，提取能量、熵、反差和相关4类典型参数，分析磁记忆和表面纹理特征的疲劳损伤时序变化规律。

通过数据层磁记忆特征和表面纹理特征的损伤映射，以及指标层基于证据理论方法的信息融合，建立了数据层和指标层两层特征融合模型。利用融合评估结果实现再制造毛坯损伤状态的预判。

本文例证为疲劳试样，损伤过程的人为干预导致数据层融合精度较高，对于具体的零部件，其拟合及预测精度有待进一步开展研究。此外，例证中各损伤区间及其边界的划分具有一定主观性，在工程中需针对具体零部件通过多次优选确定。本文所述内容为再制造毛坯损伤状态的有效评估提供了有效的方法和模型保障，同时也为后续进行零部件再制造性能评价提供了技术支撑。