结构静态响应完备减基空间的一种构建方法

张正李剑曾钦

吉首大学物理与机电工程学院，吉首，416000

0　引言

工程结构静态响应的准确快速计算对于结构优化和反求等需要重分析的领域有着重要的意义，处理这类结构静态响应问题的有效方法之一是减基法［1-3］。减基法发展较为成熟，能够在构建的低维减基空间中快速地在线计算结构的静态响应。减基法在高效在线处理问题之前需要建立合适的减基空间，而减基空间是由对应于采样点的结构响应向量基张成的，故减基法的求解精度直接依赖于所张成的响应向量空间（减基空间）的完备性，或者说是扩展性，即减基空间扩展得越完备，减基法所获得的响应解就越接近于有限元解。

通过在参数域中采样构建减基空间，较为实用的方法有拉丁超立方法［4］等，这类随机采样方法能够使参数样本点在参数域获得合理的布局，但没有考虑对应减基空间的完备性，且缺乏相应的评判准则，较难保证所建立的减基空间具有全面的完整性。构建减基空间还有一种常用的方法，即结合贪婪算法。该方法采用渐近误差估计方式来构建结构响应的减基空间［5-6］，但该方法以响应输出函数的最大误差为准则进行样本采集，随着响应输出函数的形式发生变化，其采样的结果也会发生变化，可以说依据不同的响应输出函数，采样所形成的减基空间会表现得不一致，虽然在单个观测点会有较好的计算表现，但其响应输出函数却是人为规定的，带有一定的主观性。文献［7］利用向量子空间夹角观点有效删除了减基空间中冗余的奇异基，使结构减基计算的精度得到了提升。文献［8］借助向量子空间夹角观点研究了结构模态中特征向量基空间的采样问题，使结构减基求解取得了相对较好的计算效果，但由于使用布置参数背景点的方式来选择样本点并基于此搭建对应的减基空间，故进一步提升计算效果的幅度相对有限。

本文提出了一种构建结构静态响应完备减基空间的方法，通过算例验证了该方法的可行性和有效性。

1　减基空间的完备性分析

考虑参数化的结构静力平衡方程如下：

式中，K(μ)为结构刚度矩阵；u(μ)为结构位移响应向量，u(μ)∈U；U为对应于参数域的位移响应向量集；F为结构载荷向量；μ为参数向量，μ∈Ω；Ω为参数域。

在参数域采集N个参数样本点，得到参数采样点集合Sc,N={,,...,}，通过式（1）计算得到相应的结构位移响应向量基集合

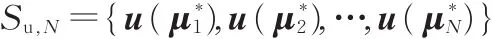
将其写为响应基矩阵形式如下：

继而针对结构变参数μ，在N维减基空间中采用减基法计算结构位移响应，可以描述为［7］

式中，αN(μ)为权系数向量；KN(μ)为N阶减基刚度矩阵；FN为N阶减基载荷向量；Ki为参数分离的刚度矩阵；σi(μ)为与参数相关的标量函数，其随着参数μ的变化而变化；BN,i和FN分别为与参数无关的N阶矩阵和向量，可存储于计算机中。

针对结构的变参数μ，结合式（2）和式（3）可在线快速求解权系数向量αN(μ)，进而通过下式获得结构的减基响应向量解：

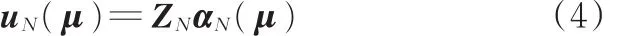
在线求解结构减基响应向量解与所采集的样本点集合及其产生的减基空间直接相关。伴随不同的采样点集合Sc,N，对应的响应向量基集合Su,N发生变化，将其张成的空间称为减基空间，并记为

故随着采样点集合Sc,N的不同，减基空间UN也不一致。由于结构的减基响应在线计算是在减基空间UN上进行的，因此减基空间UN逼近位移响应向量集U的完备度就决定了最终减基计算的精确度，而减基空间UN又完全由其响应向量基确定，即由响应向量基集合Su,N确定，故减基空间UN完备性的意义在于由响应向量基集合Su,N所张成的空间几乎能完全囊括响应向量集U。由于减基空间UN是在采样过程中形成的，因此为了获得相对完备的减基空间，不但采样过程中响应向量基是需要逐步选择、不断完善的，而且最终的采样点数N也是需要待定的。

将需在参数域Ω采样的第k个参数变量记为μk，相应的位移响应向量记为u(μk)，在此之前由k-1个响应向量基形成的减基空间记为Uk-1，则综合两者所张成的新减基空间可记为

将响应向量u(μk)与减基空间Uk-1之间的夹角表示为θ(μk)，夹角θ(μk)代表了第k个参数变量对应的响应向量与k-1维减基空间的线性相关程度，且其恒为非负值，夹角θ(μk)的值越大代表两者差异的程度越高，进而形成的新的k维减基空间U(μk)就越完备，为此产生一个在参数域搜寻对应最大夹角量值的结构优化问题，表示为

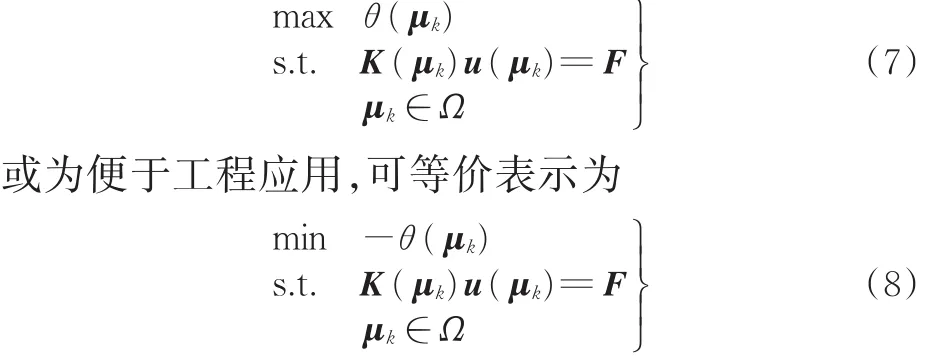
借助于式（7）或式（8）所示的优化模型，选择合适的优化算法确定相应的第k个采样参数样本点为

腹膜反折悬吊方法为手术提供了较好的手术视野，便于手术操作，15例患者后腹腔镜下肾部分切除术均顺利完成。围手术期资料见表1，平均手术时间为（88.9±24.5）min，平均肾热缺血时间为（21.4±4.6）min，平均术中出血量为（72.0±16.6）mL，平均术后住院时间为（6.9±1.2）d，术中、术后均未输血，均未发生任何重大手术并发症。

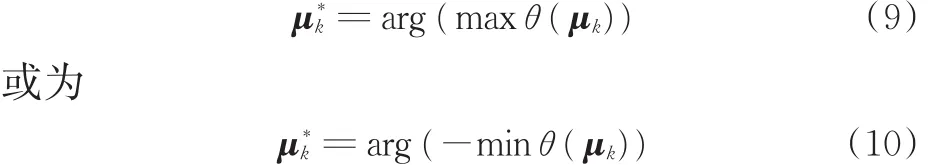
其中，函数arg（·）表示优化过程中最大函数值所对应的变量值。相应的k维减基空间为

值得注意的是，式（8）和式（10）所示的过程是在k-1维减基空间条件下确定第k个采样参数的列式，而确定第k+1个采样参数和相应的k+1维减基空间类似上述过程，依次而进，可以逐步获得趋于完备的减基空间。

在工程计算中，可根据实际精度要求将整个参数域的采样夹角阈限设定为θtol，进而确定采样过程的终止条件。如果据式（7）或式（8）在搜寻第k个采样参数向量的过程中，整个参数域的最大夹角量值小于或等于采样夹角阈限，即θ(μ*k)≤θtol，而在此之前搜寻第k-1个采样参数向量的过程中，整个参数域的最大夹角量值大于采样夹角阈限，即θ(μ*k-1)＞ θtol，则可终止构建减基空间的采样过程，而最终的采样点数为N=k。

2　完备减基空间的构建

通过上述分析可知，本文所提的减基空间构建方法可以描述为如图1所示的计算流程。

图1　减基空间的构建流程图Fig.1　The construction flow chart of reduced basis space

在图1所展示的减基空间构建流程中，每个模块的计算过程具体描述如下：

（1）采样点初始化。在参数域随机采取m（m＞1）个参数样本点，设置k=m+1，则k-1=m，形成初始参数样本点集合Sc,k-1及据式（1）形成位移响应向量基集合Su,k-1，且设定采样夹角阈限θtol。

（2）采样优化过程。据式（8）所示的优化模型及式（10），选择合适的优化算法获得第k个参数样本点以及与其对应的结构静态响应u()。

（3）采样判别过程。据向量空间夹角含义，如果响应向量u()与减基空间Uk-1之间的夹角值θ(＞ θtol，则需继续采样，进行步骤（4），否则跳转至步骤（5）。

（5）采样输出结果。获得最终的采样点数N=k及其对应的位移响应向量基集合Su,N，进而形成减基空间中的响应基矩阵ZN，停止采样算法。

3　实例分析

考虑如图2所示的平面应力结构，结构尺寸：l=1.6 m，w=0.5 m，厚度为0.02 m。结构的两端固定，施加竖直向下的载荷f1=f2=f3=1 MN。定义结构的变参数向量为 μ≡(E,ν)∈Ω,Ω=(10,250)×(0.1,0.3)，其中，E为弹性模量（GPa），ν为泊松比。将此结构用三角形单元离散，形成2 066个自由度的结构系统。

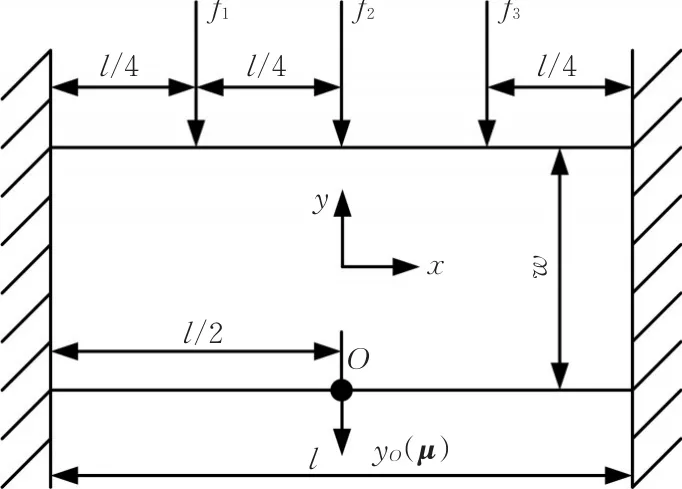
图2　平面应力结构算例Fig.2　The example of plane stress structure

针对该结构算例，在参数域Ω随机采样2个样本点，据式（1）求解其对应的有限元位移响应解，形成初始参数样本点集合Sc,2及位移响应向量基集合Su,2，且设定采样夹角阈限θtol=10-6。据式（8）和式（10）形成搜寻第k（k=3）个参数样本点的优化列式，为

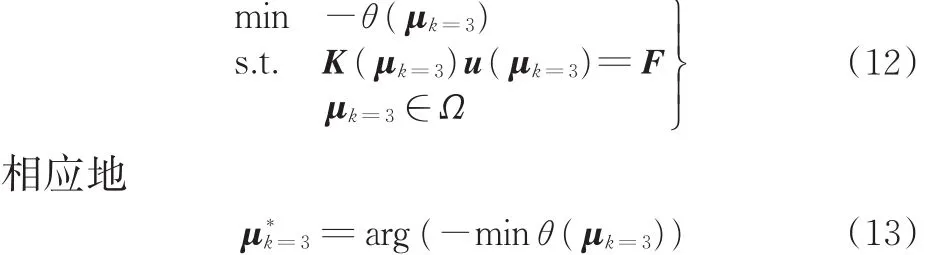
据图1所示的减基空间构建流程，利用遗传算法［9］并依据式（12）和式（13）所示的优化列式，在参数域Ω搜索获得第3个参数样本点，同时利用式（1）计算对应的结构位移响应解u()。在使用遗传算法搜索、采样第3个参数样本点时，将遗传算法的种群个体数设为30，最大迭代数置为90，其他条件定为默认值，算法搜索迭代的过程如图3所示。图3所示迭代过程最终获得的最大夹角值为θ(=5.218 37×10-4，由于其大于初始设定的采样夹角阈限θtol=10-6，故而将参数样本点加入集合Sc,2形成新的采样点集合Sc,3，并将对应的u(μ3*)加入集合Su,2形成新的位移响应向量基集合Su,3。

将k的值增加1，且保持已设置的遗传算法条件不变，使用算法继续搜索采样第k（k=4）个参数样本点μ*4以及计算其对应的位移响应u()。遗传算法搜索采样第4个和第5个参数样本点的进程与搜索采样第3个参数样本点的迭代过程类似，相应的遗传算法搜索过程如图4和图5所示。需要注意的是，随着选取初始参数点的不同以及遗传算法本身迭代的随机性，每次利用遗传算法搜索采样参数样本点的迭代过程也会有所不同。由图4和图5可以看出，算法进行到搜索采样第5个参数样本点时，最大夹角量值为θ()=2.678 21×10-7，小于初始设定的采样夹角阈限θtol=10-6；而算法搜索到的第4个参数样本点时，所对应的最大夹角值为θ(μ*4)=2.700 54×10-6，该值大于采样夹角阈限θtol=10-6。由此，当采样算法进行到采集第5个参数样本点时就会满足所设定的终止条件，最终据此获得的这5个参数样本点对应的减基空间与参数域中任一参数所对应的位移响应之间的夹角均小于θtol（θtol=10-6）。从工程实践的角度来审视，由此采样算法生成的减基空间已近乎完全覆盖结构参数域所对应的位移向量解集。

图3　遗传算法搜索第3个参数样本点的迭代过程Fig.3　The iteration process of genetic algorithm for searching the third parameter sample point

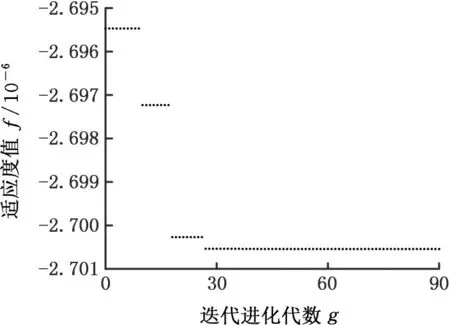
图4　遗传算法搜索第4个参数样本点的迭代过程Fig.4　The iteration process of genetic algorithm for searching the fourth parameter sample point

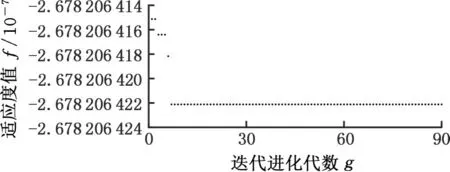
图5　遗传算法搜索第5个参数样本点的迭代过程Fig.5　The iteration process of genetic algorithm for searching the fifth parameter sample point

将图2中结构的O点作为结构响应的输出观察点，相应于变参数向量μ∈Ω，将μ竖直向下的有限元位移响应记为yO(μ)，N个基条件下的减基法位移响应记为yNO(μ)。在参数域Ω随机采集nc=200个参数点作为参数测试点Tc={μ1,μ2,...,μ200}，利用有限元法计算这些参数测试点对应的结构整体位移响应u(μ)(μ∈Τc)和结构O点处响应yO(μ)(μ∈Tc)。同时，利用减基法在上述采样响应基所构建的减基空间中依次计算这些参数测试点对应的结构整体位移响应=3,4,5(μ)(μ∈Τc)和 结 构O点 处 响 应=3,4,5)(μ)(μ∈Tc)。将由有限元法与在不同减基空间中由减基法获得的计算结果进行比较，并定义结构响应的整体平均相对误差为

相应的平均相对误差对数图见图6。

图6　不同基数的减基空间中结构响应的平均相对误差Fig.6　The average relative error of structural response in the base space with different dimension

从图6可以看出，减基法计算结果的整体和局部平均相对误差均随着采样基数的增加呈现对数性态式的快速下降，最终产生的整体和局部平均相对误差也均在10-9量级左右，说明本文方法具有样本采集的精准性，能够逐步构建出完备的减基空间，并且有着极佳的计算收敛效果。同时也应注意，使用减基法结合本文方法进行结构响应计算时，其求解误差不但与工程设定的夹角阈限有关，也与计算机的实际字长有关，换言之，子空间的夹角阈值与计算机的有限字长共同决定了减基计算的精确度。

4　结论

本文从向量子空间夹角的观念出发，针对结构静态响应的减基计算过程，提出一种既能分析减基空间完备性又能构建完备减基空间的采样方法。该方法能够精准地选择减基空间的完备基，可以避免奇异基的出现，并且其构建过程与初始参数样本点的选择无关。该方法构建减基空间的过程是收敛的，而且由其产生的减基法计算误差也是收敛的，从而保障了减基法分析结构静态响应的计算可靠性。文中算例验证了该方法的有效性。