大曲率短线匹配连续刚构桥空间几何线形控制
2018-07-17侯文崎崔大鹏
罗 锦,侯文崎,崔大鹏
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 中铁大桥局集团 第二工程有限公司,江苏 南京 210015)
短线匹配预制拼装桥梁因其在环境保护和施工工期方面的优势,在城市高架和市政桥梁应用日趋广泛,其中不乏曲线桥梁[1−4]。高精度几何线形控制是短线匹配预制拼装桥梁的关键技术之一,贯穿梁段预制和架设全过程[4−5]。对于曲线预制拼装桥梁,特别是大曲率桥梁,主梁空间线形控制精度不仅影响桥梁美观,还直接影响桥梁受力状态,甚至运营安全[1,6−7]。现有国内外规范都对短线匹配预制拼装桥梁的几何线形控制精度提出了严格要求[8−10]。但受环境温度、混凝土收缩徐变、施工振捣、预应力张拉等因素影响,梁段线形在预制和拼装架设过程中存在各种误差,主要有节段梁长和转角误差、横坡误差和平移误差等。美国ASSHTO桥梁施工规范[9,11]明确规定:“除了按所确定的浇筑曲线计算竖向和水平偏转外,还应采用所测量的单个单元的横坡来计算累积扭转曲线以核对推定的偏转。在计算密接浇筑过程的装配标高中,应优先考虑采用适当反转修正扭转误差的方法。密接浇筑状态下的节段应不承受扭转产生的应力。国内外研究者对短线匹配施工桥梁几何线形误差修正方法进行了相关研究[12−16]。方蕾[12]基于直接修正法[13],提出在制造梁段局部坐标系下修正梁长和角度误差,但未考虑梁段横坡影响,标高控制精度欠佳。周凌宇等[15]考虑梁段局部坐标系和整体坐标系的实际不重合,对文献[12]的算法进行了优化,相对文献[12]提高了标高控制精度。文献[16]在文献[15]的研究基础上,考虑了匹配梁段偏离理论位置的横坡误差,进一步优化了几何线形控制算法。直接修正法是在当下浇筑节段一次性地将误差修正,简单直观。尽管如此,节段预制拼装桥梁几何线形控制仍存在以下问题:1) 没有实现真正三维空间的几何线形控制,如对梁段转角误差修正是将其在水平面和竖平面投影之后分别修正再叠加,没有考虑其在两个平面投影的空间耦合效应,当桥梁所处线路与竖平面的夹角越接近直角,这种方法对梁段转角误差控制精度越差;2) 文献[16]虽然考虑了匹配梁段的横坡误差,但将该横坡误差简化为现浇节段拼装时的横坡误差,当桥梁所处线路曲线半径越小,这种方法对梁段横坡误差的控制精度越差;3)既有研究中,都没有考虑相邻梁段预制完成后的平移误差。针对上述问题,本文将基于直接修正法[13],考虑梁段长度和转角误差、横坡误差和平移误差,提出一种能够同时适用于直线和大曲率短线匹配施工桥梁的几何线形三维控制方法,并结合某在建(4×40)m大曲率短线匹配连续刚构桥的几何线形控制,将本文方法的控制结果与实测结果进行对比,以验证本文方法的准确度和精确度。
1 基本概念和坐标系的定义
空间坐标系下,梁段空间几何线形可通过梁段顶面中心线 2点坐标和固定端模侧接缝横坡来确定[13],前者称为梁段的线形,后者称为梁段的姿态。实际工程中,每个梁段的空间几何位置通过如图 1所示的6个控制测点来实现。图中,FH和BH是水平控制点,反映梁段线形的X和Y坐标控制;FL,BL,FR和BR则为高程控制点,反映梁段线形的Z坐标和梁段姿态控制。
梁段预制时,将已预制成型的匹配段的空间几何位置,经过2次空间坐标变换(局部坐标系→整体坐标系→局部坐标系),得到其与相邻待浇梁段之间的相对几何位置关系,通过调整匹配段与待浇段的相对空间位置(误差修正),控制下一相邻梁段的预制线形。
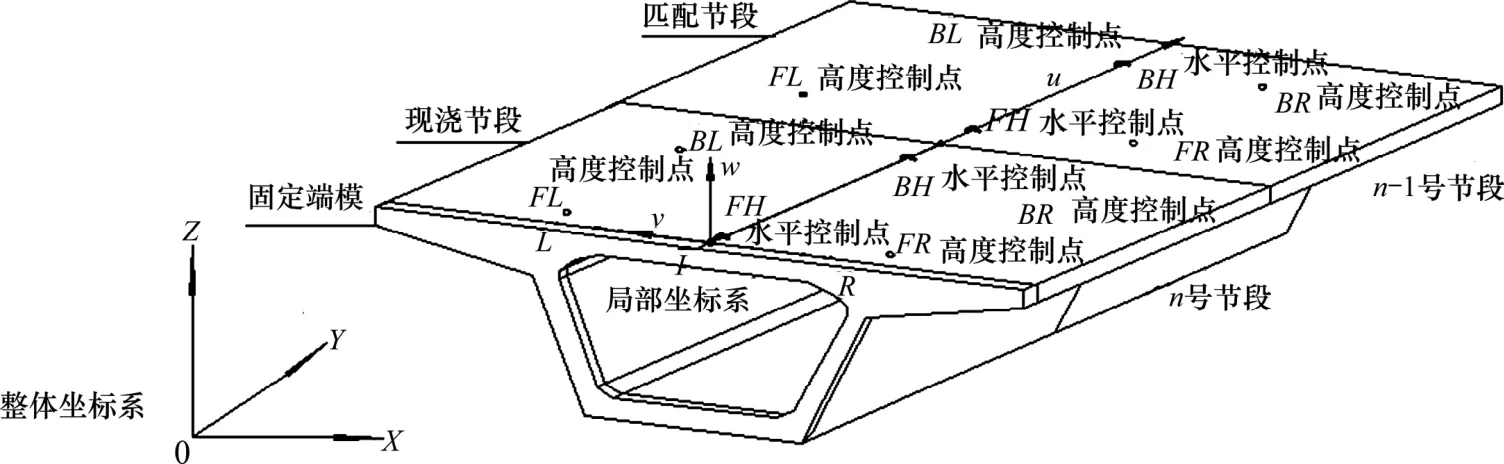
图1 相邻节段梁坐标系和控制测点示意图Fig.1 Diagram of the coordinates and controlling points on adjacent segmental girders
整体坐标系选取广州当地城建坐标系,记为O - XYZ;局部坐标系 I -uvw建立于每个梁段自身。以梁段顶面中心线在固定端模侧为I端,另一侧活动端为J端,取I端侧梁段顶面和横截面交线上任意点→则局部坐标系原点为I, 矢量方向为u轴,IL 矢量方向为 v轴,根据右手系得到 w轴,详见图1。记n−1号梁段为匹配段,n号梁段为现浇节段,i为梁段上的各控制测点(i=FH,BH,FL,BL,FR和BR),则n−1号节段的2次坐标转换计算如下。
1) n−1号梁段从自身局部坐标系到整体坐标系:
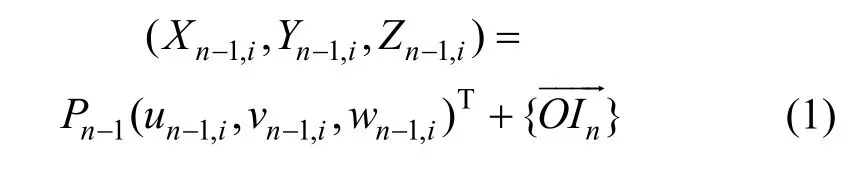
2) n−1号梁段从整体坐标系到n号梁段局部坐标系:
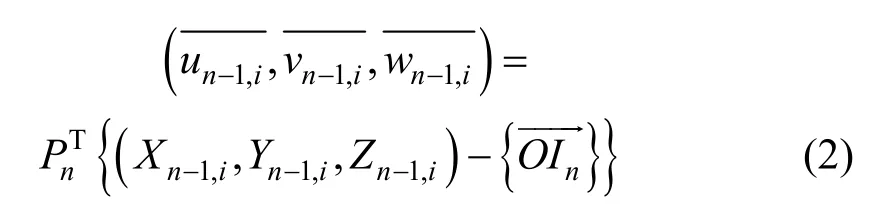
2 误差修正基本原理
图2为相邻梁段误差修正示意图,其中2(a)为预制阶段相邻梁段相对几何位置关系示意图,2(b)为拼装阶段相邻梁段相对几何位置关系示意图。
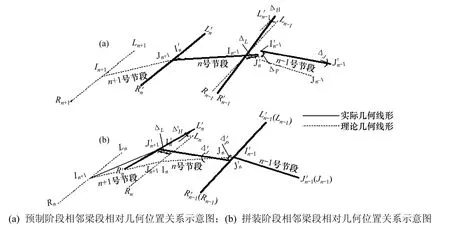
图2 相邻梁段误差修正示意图Fig.2 Diagram of geometry error correction of adjacent segmental girders
图 2(a)中,n−1号梁段匹配时实际位置相比理论位置存在转角误差 ΔJ,横坡误差 ΔH和平移误差ΔP。n号梁段预制完成后,其实际长度相比其理论长度的差值为ΔL。此时,n号梁段与n−1号梁段已经匹配完成,二者的相对几何位置关系也已确定,且在后续过程保持不变。
图2(b)中,各梁段按序依次拼装。n−1号梁段仍在理论位置完成拼装。因两者的相对几何位置关系保持不变,故其拼装的实际位置相应变化到In′Jn′和′处,相对其理论位置InJn和RnLn,存在梁长误差′,转角误差′,横坡误差和平移误差。此时,通过修正整体坐标系下n号梁段节点 In′的坐标和横坡Rn′Ln′,得到更新后的n+1号梁段的理论空间几何线形。
下文按照预制阶段梁长和转角误差、横坡误差、平移误差的顺序依次说明各种误差的修正计算。在完成下面误差修正计算过程中,需要将已知n−1号节段匹配时6个控制测点i(i=FH,BH,FL,BL,FR,BR)的实测坐标 (),按式(5)转换到整体坐标系中。
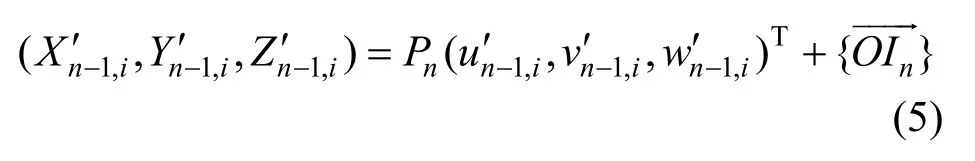
3 各种误差修正方法
3.1 梁长和转角误差修正
图3为相邻梁段梁长和转角误差修正示意图。其中3(a)为预制阶段相邻梁段相对几何位置关系示意图,3(b)为拼装阶段相邻梁段相对几何位置关系示意图。
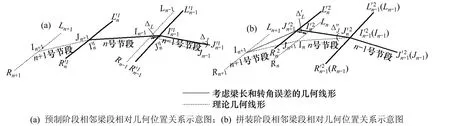
图3 相邻梁段梁长和转角修正示意图Fig.3 Diagram of length and angle error correction of adjacent segmental girders
修正梁长和转角误差计算步骤如下:
1) 投影平面的确定,由式(1)可得 n−1号梁段控制测点BH和FH理论匹配整体坐标。沿整体坐标系Z轴方向,任取其中一点的非零增量Δ,可以确定第三点的整体坐标,由此三点可确定平面A1。同理,由式(5)可得n−1号梁段控制测点BH和FH实际匹配整体坐标,按照相同方法确定平面A2。
2) 误差角的计算,n−1号梁段匹配时转角误差ΔJ的水平分量ΔJ,XY和竖向分量ΔJ,Z。
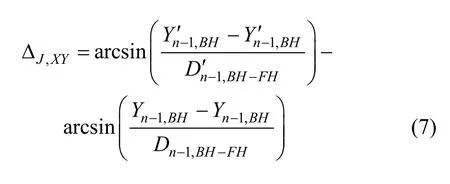

3) n−1号梁段匹配的实际位置对应的线形计算,如图3(a)中n−1号梁段节点的整体坐标计算如下:

4) n号梁段拼装的实际位置对应的线形计算,根据 n号梁段与 n−1号梁段相对空间位置不变关系,则整体坐标计算如下:
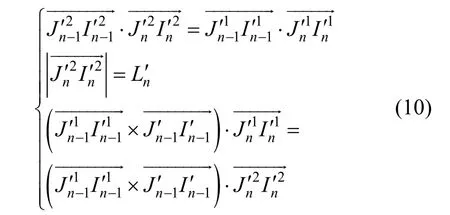
式中:nL′为n号梁段实测梁长。
3.2 横坡误差修正
图4为相邻梁段横坡误差修正示意图。其中4(a)为预制阶段相邻梁段相对几何位置关系示意图,4(b)为拼装阶段相邻梁段相对几何位置关系示意图。可以看出预制阶段的横坡误差 ΔH会引起拼装阶段的横坡误差和转角误差Δ ′H,J。
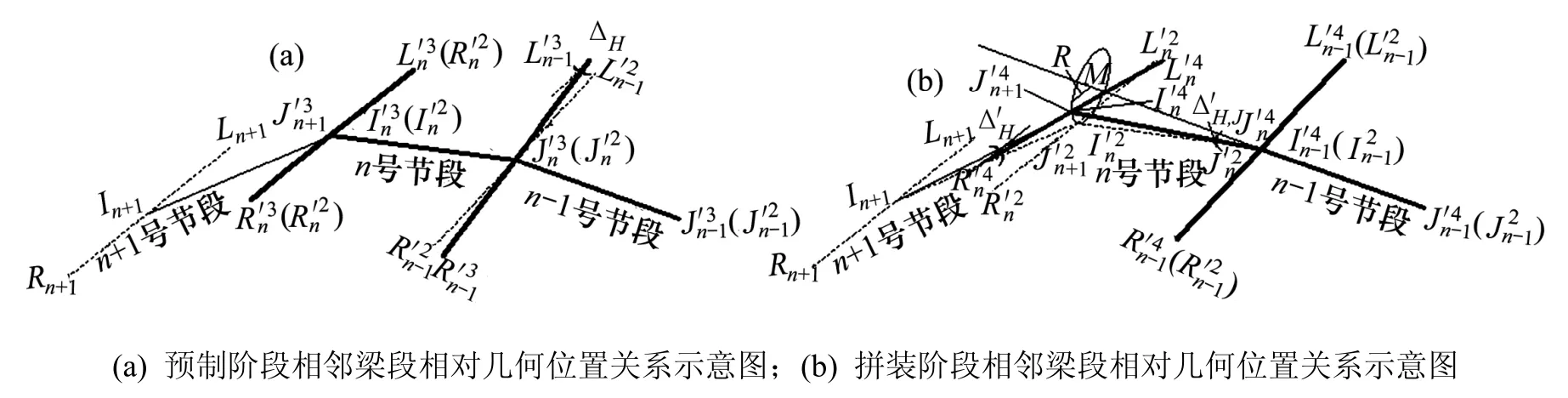
图4 相邻梁段横坡误差修正示意图Fig.4 Diagram of transverse grade error correction of adjacent segmental girders
进一步修正横坡误差计算步骤如下:
1) 计算预制阶段 n−1号匹配梁段的横坡误差ΔH,从固定端模侧看,顺时针为正。
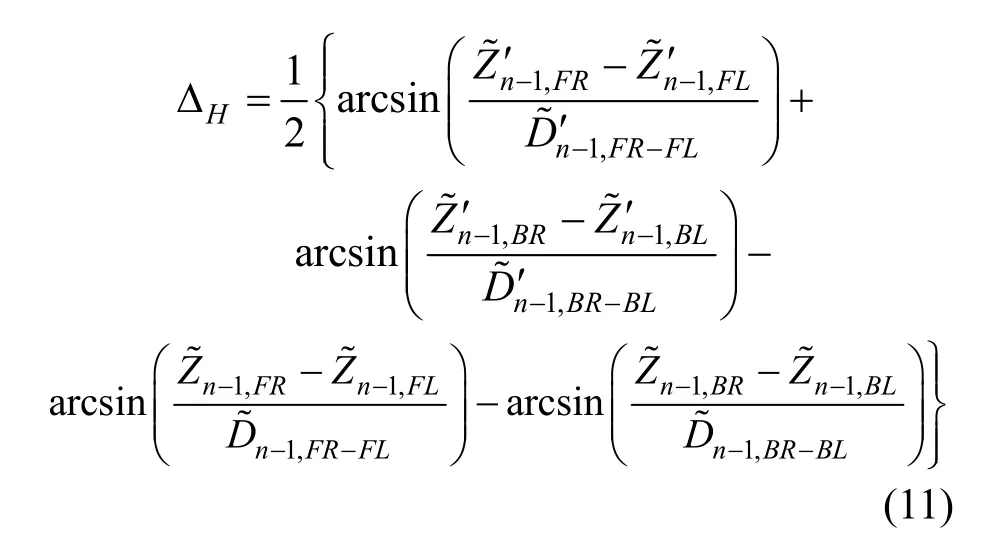
式中:z~n-1,i和z~n′-1,i分别为 n−1号梁段位于实际匹配位置和理论匹配位置时,控制测点i在平面A3上投影的Z坐标,平面A3为以梁顶面中心线方向为法线并过端点I;和分别为n−1号梁段位于实际匹配位置和理论匹配位置时,右侧高程控制测点i和左侧高程控制测点j的间距在平面上投影(i= FR, BR;j=FL, BL)。
2) n号梁段拼装的实际位置对应线形和横坡的计算。根据n号梁段与n−1号梁段相对空间位置不变关系,考虑横坡误差Δ′H和转角误差,修正后的横坡和整体坐标分别按式(12)和(13)计算。

式中:R为图 4(b)中所示半径;M 为平面 A3与)延长线的交点;θ 为理论横坡;n,H= a rctg(tan ΔH/cos(an,n-1)), an,n-1为图4(a)中之间的夹角,由余弦公式易得。
3.3 平移误差修正
图5为相邻梁段平移误差修正示意图。其中5(a)为预制阶段相邻梁段相对几何位置关系示意图,5(b)为拼装阶段相邻梁段相对几何位置关系示意图。

图5 相邻梁段平移误差修正示意图Fig.5 Diagram of translation error correction of adjacent segmental girders
进一步修正平移误差计算步骤如下:
1) 空间坐标转换,在3.1和3.2误差修正的基础上,重新确定坐标转换矩阵将n−1号节段实测匹配坐标转换到整体坐标系,则有:
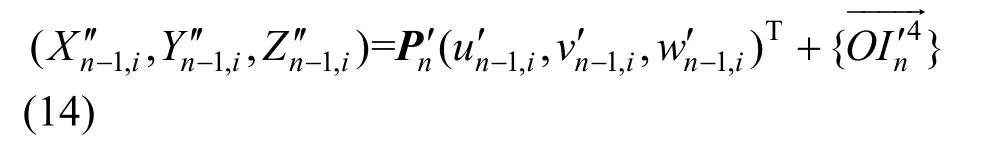
2) 计算平移误差ΔP,在整体坐标系下的平移误差为:
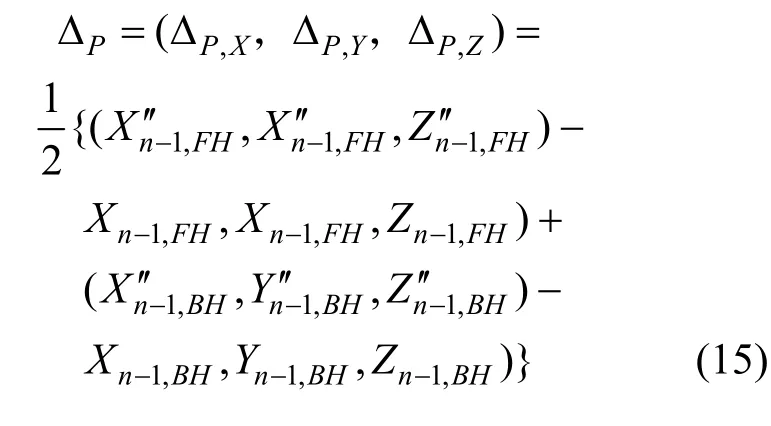
3) 计算n号梁段拼装的实际位置对应的线形,根据 n号梁段与 n−1号梁段相对空间位置不变关系,修正后整体坐标计算如下:

至此,确定了n号梁段考虑梁长和转角误差、横坡误差和平移误差后拼装的实际位置的几何线形,更新n+1号梁段理论空间几何线形。
3.4 与既有误差修正方法的对比
本文和文献[16]算法最大差别在于现浇梁段拼装时的实际位置的确定。分别采用本文算法和文献[16]算法对转角误差ΔJ修正,以对比分析2种算法的修正效果。
以图3为例,参考《城市轨道交通工程项目建设标准》,假设该桥主梁位于半径为360 m的圆曲线上,梁顶面不设横坡和超高。图3(a)中n−1号和n号梁段的理论线形的I端和J端的整体坐标分别(2.599 5,0.051 0,0.000 0),(5.200 0,0.120 0,0.005 0),(0.000 0,0.000 0,0.000 0)和(2.599 5,0.051 0,0.000 0)。n−1号梁段匹配时转角误差ΔJ为:ΔJ,XY=0.001 538 35 rad;ΔJ,Z=0.001 9220 6 rad,横坡、平移误差为 0。n号梁段不存在梁长误差。分别采用本文算法和文献[16]算法,修正转角误差ΔJ,计算结果见表1。
由表1可见:1) 现浇梁段预制完成后,与对应匹配梁段的相对位置关系便已确定,两梁段之间的夹角则应在预制阶段和匹配阶段保持不变。如表 1所示,本文算法计算所得预制阶段和拼装阶段n−1号和 n号梁段夹角差 Δα=0,符合上述实际情况;而文献[20]算法计算所得Δα≠0,与实际情况不符。这说明,文献[16]算法中,对转角误差ΔJ将其在水平面和竖平面投影之后分别修正再叠加的做法,降低了误差修正精度。2) 由于上述原因,导致文献[16]算法对标高的控制精度不高。对比表中2种算法计算所得n号梁段节点的整体坐标,发现二者在标高Z方向的差值达到1.7 mm,X和Y方向的差值均小于0.1 mm。

表1 40 m跨度曲线节段预制拼装桥梁转角误差ΔJ修正计算结果对比(曲线半径360 m)Table1 Comparison of the calculation results of the angle error correction of 40 m span curve precast segmental bridge (Curve radius 360 m)
4 (4×40) m 大曲率连续刚构桥几何线形控制
某在建(4×40) m连续刚构桥位于圆曲线半径为804.2 m的线路上,该孔跨对应墩号XT84~XT88,主梁采用短线法预制,逐孔整跨拼装施工。采用本文算法对该桥进行空间几何线形控制,并将实测控制结果与理论线形对比,进一步验证本文算法的正确性和精确性。
选取该桥其中一孔40 m跨为例,该孔跨对应墩号为 XT86~XT87,节段划分如图 6所示。主梁节段分为端头节段(D类)、过渡节段(G类)及标准节段(B类)3种类型。该孔部分节段控制测点实测坐标与理论坐标对比详见表 2,碍于篇幅限制,只给出端头块和跨中块的对比。表中各梁段控制测点的整体坐标X和Y均已转化为局部坐标系(图6)下的X′和Y′坐标。图7为成桥后梁段高程和轴线实测值与理论值的偏差沿梁长分布曲线。

图6 XT86~XT87孔节段划分Fig.6 Segmental girder division of the XT86~X87 bridge
由表2和图7可见:1) 采用本文算法所得几何线形控制效果为:实测主梁轴线偏差最大不超过 6 mm,高程偏差最大不超过11 mm,均远小于规范[8,10]的规定限值,验证了本文算法的精确性。2) 几何线形控制中有必要考虑节段平移误差修正。如图7(a)和图7(b)中的B35和B36等节段所示,在节点处存在2个不同的偏差值,两者相差最大达到了将近2 mm,说明平移误差是存在的,必须予以修正控制以使主梁线形满足设计要求。

表2 40 m孔跨各梁段几何线形控制实测坐标与理论坐标对比Table2 Comparison between the measured data and theoretical data of geometric control on the 40 m span segmental girder
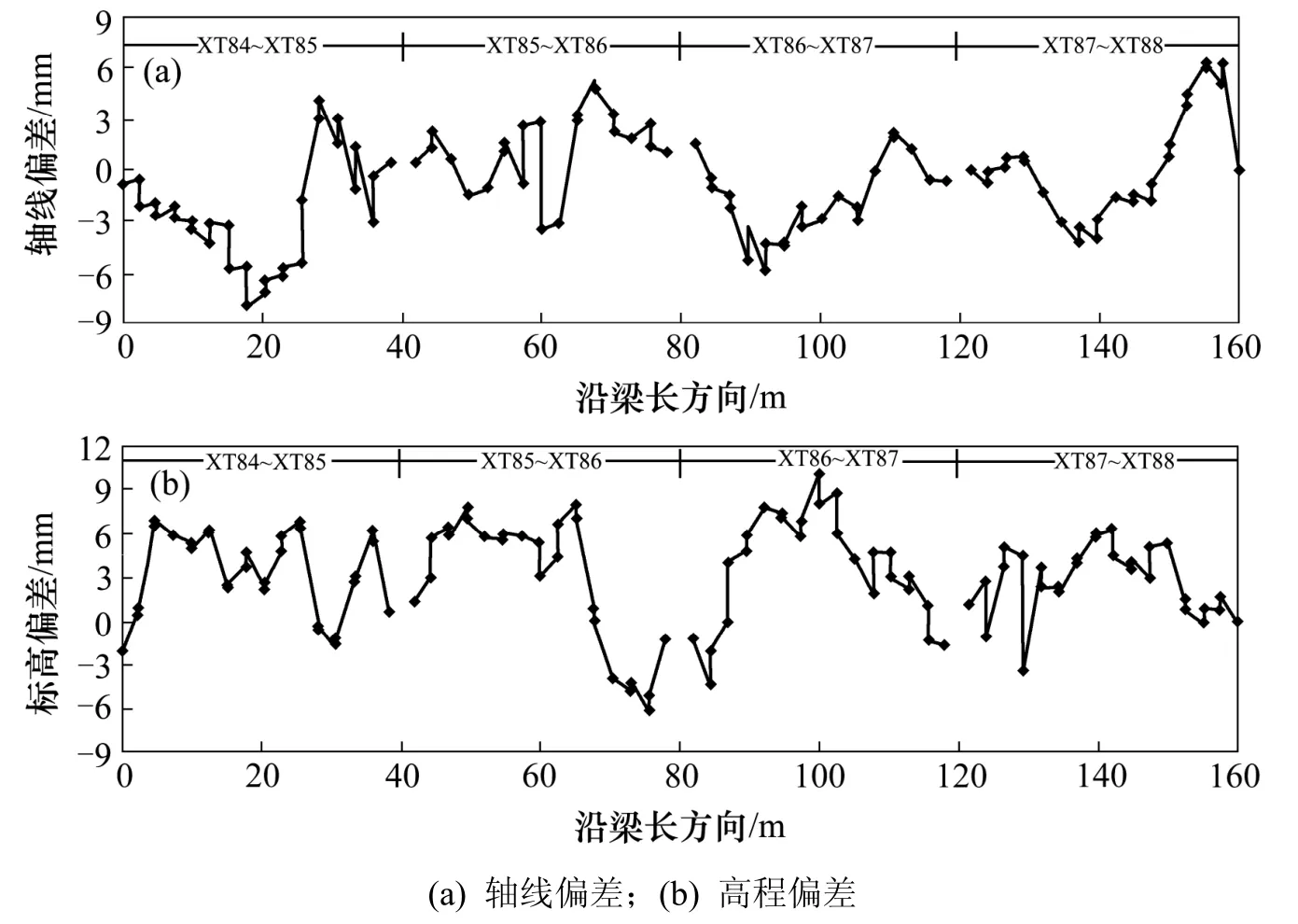
图7 成桥后节段各节点轴线和高程偏差Fig.7 Height and axis deviation of segment’s node after completion of bridge
5 结论
1) 针对大曲率短线匹配连续刚构桥几何线形控制,基于三维空间坐标系,充分考虑梁段长度和转角误差、横坡误差和平移误差,提出一种能够同时适用于直线和大曲率短线匹配施工桥梁的几何线形三维控制方法。该法可实现及时修正每个梁段预制和拼装的空间线形,避免了误差累积,达到高精度几何线形控制的目的。
2) 与既有算法对比表明,本文算法符合现浇梁段与对应匹配梁段的相对位置关系在预制阶段和拼装节段保持不变的实际情况,控制精度有保证。既有算法由于对转角误差 ΔJ将其在水平面和竖平面投影之后分别修正再叠加,降低了误差修正精度,特别是标高控制精度。
3) 工程实例表明,采用上述几何线形三维控制方法,实测主梁线形与设计线形相比,轴线偏差最大不超过6 mm,高程偏差最大不超过11 mm,均远小于规范的规定限值,验证了本文方法的正确性和精确性;另外,平移误差实际存在,应予以修正以提高几何线形控制精度。
