基于支持向量机的轨道不平顺预测研究

于　瑶，刘仍奎，王福田

(北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

轨道不平顺状态对于列车运行安全和旅客乘车舒适度至关重要[1]。随着铁路快速发展，列车速度大幅提升，轨道结构承受来自列车荷载作用，会加速轨道的劣化。对轨道不平顺的发展规律进行预测是近代轨道力学的基本课题，也是合理安排养修周期，全面推进轨道的“状态修”，降低养修成本，保证线路安全和平顺的关键，可为轨道养护维修计划提供决策参考[2]。目前，许多专家和学者将线性回归[3]，综合因子[4]，灰色理论方法[5]等方法引入到轨道不平顺预测研究中，并取得了良好的效果。白文飞等[6]通过利用 BP神经网络强非线性能力，采用递推合成BP神经网络方法对轨道不平顺进行预测，提高了预测精度。李巍[7]针对所采集的轨道不平顺状态数据异常的问题，在灰色预测与回归分析预测的基础上，利用熵值法，计算组合预测加权平均系数，提出了基于熵值法的轨道状态组合预测模型。林怀青等[8]采用主成分分析和支持向量机相结合的方法对轨道不平顺状态进行识别，并通过对不同轨道不平顺下轴箱加速度的分析，验证该方法的有效性。为了快速预测轨道列车的振动状态，徐磊等[9]提出基于PCA-SVM方法的车体振动状态分类预测模型。支持向量机的方法可以得到全局最优解，具有很强的非线性拟合的能力，可以解决神经网络收敛速度慢和无法避免局部最优的问题。该方法的基本思想是，通过非线性映射，把样本空间映射到一个高维的特征空间，使在特征空间中可以应用线性学习的方法解决样本空间中的高度非线性分类和回归等问题[10]。本文针对轨道不平顺预测问题，通过利用支持向量机的泛化能力，将此方法引入到轨道不平顺状态的研究中，并建立支持向量机轨道不平顺预测模型。然后利用此模型对测试样本进行建模并预测，并将结果与文献[6]进行了比较。从对比结果可以明显看出，该模型在轨道不平顺预测中具有良好的可靠性和适用性。

1　轨道不平顺状态描述

轨道整体不平顺状态通过轨道质量指数(TQI)来表示。实践证明，该指数对于维护铁路的轨道质量状态、保证列车平稳安全运行起到了重要作用。我国的轨道质量指数是通过对200 m单元区段内的轨距、高低、轨向、三角坑等7个项目的不平顺幅值做标准差求和得到的。这7个项目的数据是由轨检车对轨道进行动态检测得到的，每当轨检车检测完成后，会自动形成轨道线路的原始检测数据以及每200 m长度的TQI数据检测结果，一段时间后，就会形成一个TQI序列集。TQI计算公式如下：

其中：σi为各单项轨道不平顺的标准偏差；为连续采样的平均值；xij各单项不平顺的幅值。从式(1)可知，TQI值的大小与轨道平顺状态密切相关，即其数值越大，表明轨道的平顺程度越差。管理者通过观察该指数数值大小，不但可以了解轨道的劣化程度，而且可以通过对所有轨道单元区段TQI数值排序来确定需要重点维修的轨道区段。

2　支持向量机轨道不平顺预测模型建立

由于每个轨道单元受各种异质性因素影响，各个轨道单元的TQI数据的变化规律是不同的。本文的建模思路是针对每一个单元区段个性化的建立一个其自身的数据变化规律模型，利用该单元区段的历史数据所形成的序列来寻找该单元区段的变化规律，具体的思路是采用支持向量机的方法来建模。支持向量机的回归拟合的思想是寻找一个最优分类面使得所有训练样本离该分类面的误差最小。本文所构建的基于支持向量机的轨道不平顺预测模型建立以及性能评价，可以分为以下几个步骤，如图1所示。

图1　支持向量机的轨道不平顺预测模型建立流程Fig.1　Process of prediction for track irregularity based on support vector machine

其中：()tΓ为非线性映射函数。ω和a是2个变量，支持向量机思想是通过优化算法，选取支持向量机参数求解对变量ω和a的最优化问题。

定义ε为线性不敏感损失函数，线性不敏感损失函数具有较好的稀疏特性，通过选取恰当的ε可以使结果有较好的泛化能力，选取损失函数为：

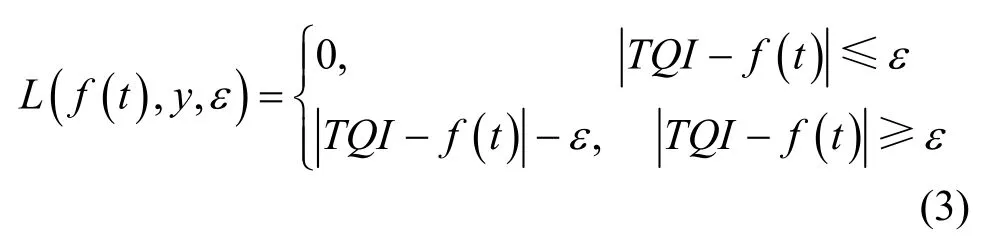
其中： f (t)为回归函数返回的TQI预测值，TQI为对应的TQI真实值。

为了得到式(2)中的ω和α，引入松弛变量τi，构造如下约束条件：

其中：C为惩罚因子，C越大表示对训练误差大于ε的样本惩罚越大。求解式(4)可得

其中：N为支持向量个数。

3) 数据预测。通过利用第1部分TQI数据建立的模型，来预测轨道质量状态未来的发展趋势。

结合式(4)，式(5)和式(6)，可得回归函数为

从式(7)可以看出支持向量机的结构与神经网络的结构比较类似，其结构图如图2所示。

图2　支持向量机的结构图Fig.2　Structure of support vector machine

4) 性能评价。根据选取的性能指标对预测结果进行评价。

为了检验预测模型的预测效果，选取评价指标均方误差E和决定系数R2，来对建立的预测模型进行性能评价。均方误差的值越小，说明预测模型具有较好的精度。决定系数越接近 1，表示所建立的模型参考价值越高；相反，越接近0时，表示参考价值越低。其计算公式如下：

3　案例分析

3.1　TQI预测模型建立

本文利用济南铁路局管辖范围内京九线 2008年2月～2010年7月的轨检车检测数据，选取100个200 m长的轨道单元区段的TQI数据，分析其轨道不平顺发展趋势，建立基于支持向量机的轨道不平顺预测模型，将预测结果与文献[6]中的BP神经网络方法预测结果进行对比，以说明其有效性。首先以具有代表性的2008年2月～2010年7月的京九线下行 K467+400～K467+600单元区段为例说明建模过程，该单元区段的TQI检测数据如表1所示。

从表1可以看出，在第10次(2008年11月)和第11次(2008年12月)2次检测之间，轨道的TQI值急剧减小，说明第 10次检测之后对轨道进行了维修作业，使得轨道质量状态转好。以此为分界点，将TQI数据按照2个周期考虑。本文针对京九线下行K467+400～K467+600单元区段TQI的变化，通过利用Matlab分别对表1中的轨道质量指数进行模型建立和预测。

表1　京九线下行K467+400～K467+600单元区段TQI数据表Table1　TQIs of Jingjiu Railway Line’s K467+400～K467+600

在第1个周期内，选取前7个数据作为训练样本，在第2个周期内选取前17个作为训练样本，分别建立预测模型，预测模型结果如图3(a)和3(b)所示。

3.2　对TQI发展趋势预测

通过利用3.1中所建立的预测模型，在第1个周期内选取后3个样本为性能观测指标。在第2个周期内后3个样本作为观测指标，得到的预测结果图如图4(a)和4(b)所示。

通过预测结果可以计算得到性能评价指标，如表2所示。根据式(8)计算，2个周期预测模型的均方误差和决定系数分别为 E=0.012，R2=0.98和E=0.008，R2=0.97，可以明显看出该方法均方误差比较小，而且决定系数接近 1，可以证明该方法建立的预测模型是有效的。

3.3　预测结果的对比

与京九线下行 K467+400～K467+600单元区段的模型建立与预测过程类似，选取 2008年 2月～2010年 7月京九线下行 K425+000～K475+000的100个轨道单元区段的TQI数据进行预测，并将预测结果与文献[6]的递推合成BP网络预测方法的预测结果进行比较。

图3　2个周期TQI预测模型结果Fig.3　Predictive model results of TQIs for the two periods

图4　2个周期支持向量机TQI预测值与TQI实测值对比图Fig.4　Comparison of the prediction values of support vector machine and factual values for the two periods

表2　基于支持向量机的轨道不平顺预测性能评价结果Table2　Performance evaluation results of prediction for track irregularity based on support vector machine

随机抽取其中的3个轨道单元区段K467+400～K467+600，K472+600～K472+800 和 K430+800～K431+000，其利用支持向量机的预测方法得到的预测结果与文献[6]的递推合成BP网络方法的预测结果比较见表3。从表3中数据得出，本文方法所得该3个轨道单元区段TQI预测值的平均相对误差为0.97%，文献[6]方法所得TQI预测值的平均相对误差为2.04%。采用本文方法所建立的预测模型的误差精度相比于文献[6]中的预测模型的预测精度有所改善。

经过建模预测京九线下行 K425+000～K475+000的100个轨道单元区段的TQI数据，将预测结果与文献[6]的递推合成BP网络预测方法的预测结果进行比较。利用支持向量机方法得出100个轨道单元区段的TQI预测值的平均相对误差为0.85%，文献[6]方法所得 TQI预测值的平均相对误差为3.29%。从预测结果可以明显看出，相比于文献[6]中的预测方法，支持向量机的预测方法较为符合轨道不平顺的发展趋势，能够很好地反应轨道质量指数随时间变化的规律。

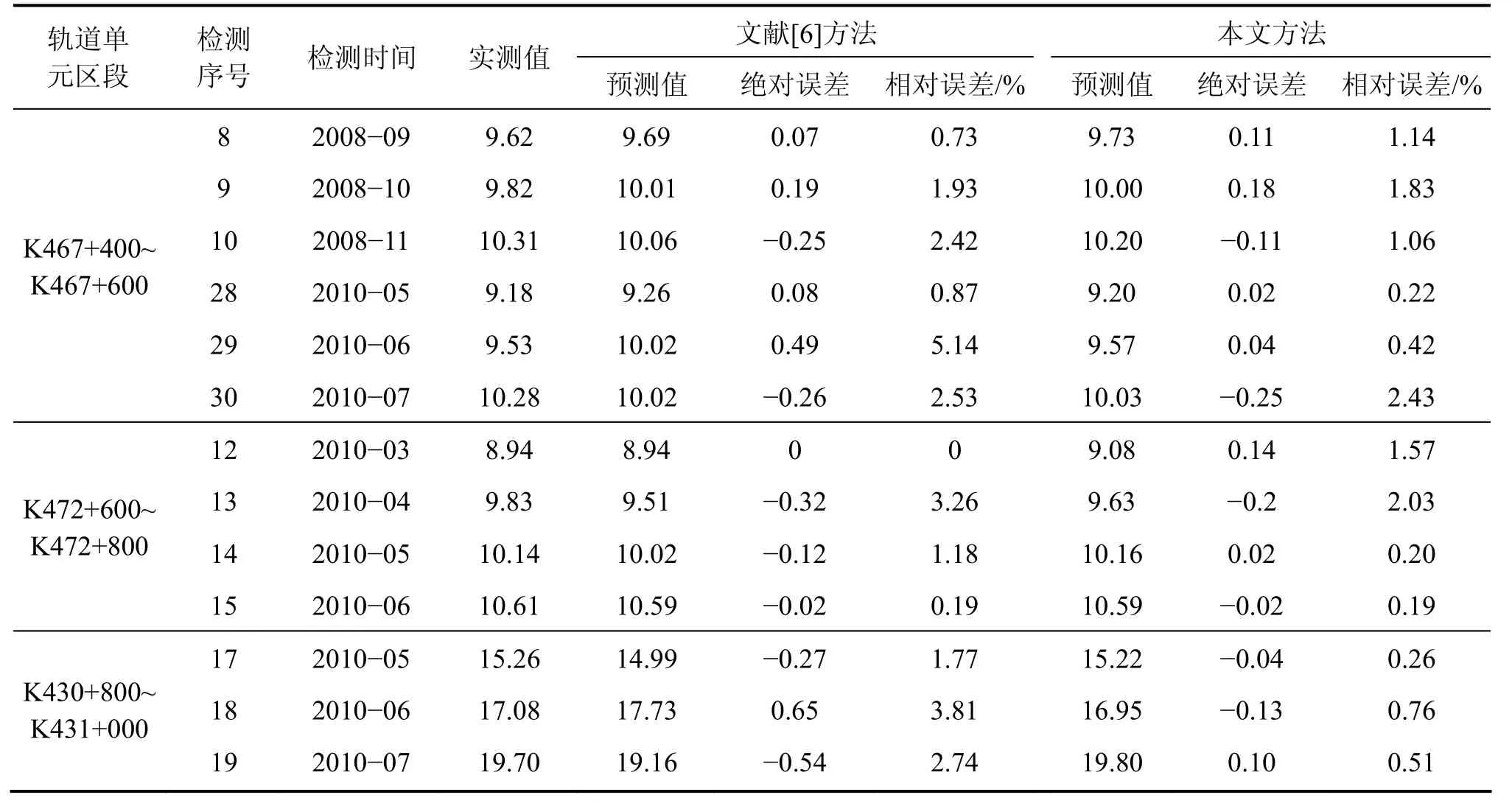
表3　2种算法的TQI预测结果比较Table3　Comparison of two algorithms for TQI prediction results

4　结论

1) 通过利用支持向量机强泛化能力，将其引入轨道不平顺预测研究中，通过对TQI序列建模预测，给出了支持向量机方法建立轨道预测模型的一般步骤和仿真预测。以京九线下行3个轨道单元区段的实际TQI检测数据为算例进行验证，该方法均方误差比较小，而且决定系数接近 1。结果表明，无论是在模型建立还是预测过程，支持向量机都具有较强的逼近能力，可以有效地对TQI进行建模预测。

2) 通过结合支持向量机的预测方法，对轨道不平顺 TQI值进行单周期预测，选取京九线下行K425+000～K475+000的100个轨道单元区段的TQI数据。利用支持向量机方法得到100个轨道单元区段的预测值的平均相对误差为0.85%，利用文献[6]中递推合成BP网络所得TQI预测值的平均相对误差为3.29%。相比于递推合成BP网络的预测方法，基于向量机的轨道不平顺预测精度相对有所提高。