“用2、5、3倍数特征”解决问题的策略研究

2018-07-16吴恢銮施娇娥

教学月刊·小学数学 2018年1期

吴恢銮施娇娥

【摘要】不同的学生解决同样的一个数学问题，由于他们的思维方式不同，可能会出现不同的解题策略。如整除问题，让学生运用“2、5、3倍数的特征”解决这个问题。发现出错原因及正确解题策略，并分析学生解决问题的思维过程。对教学启示如下：其一，关注学生数学思维能力的水平差异和类型差异，实施差异教学。其二，关注思维类型差异，渗透有序思想。其三，加强对比，理清2、5、3倍数特征关系，在综合性问题解决中实现知识求联。

【关键词】2、5、3倍数特征；解决问题；策略

一、问题提出

在同一年龄阶段，不同的学生解决同样的一个数学问题，他们的思维方式可能会有较大的差异，因此可能会出现不同的解题策略。当然解题策略既有共性又有独特性。例如，在教学2、5、3倍数的特征之后，我们想了解学生是否会综合应用“2、5、3倍数的特征”来解决实际问题。在解决问题的过程中，有多少人会错，有多少人会对？出现错误的原因有哪些？解题正确的人所采用的解题策略又会有哪些？这些问题并不十分清楚。为此，笔者给出一个整除问题：在五位数25□4□的方格内填什么数字，才能使它既能被3整除，又能被5整除？试图从学生的解题中，发现出错原因及正确解题策略，并分析学生“用2、5、3倍数特征”解决问题的思维过程。通过此题的研究，能读懂学生的思维差异，初步检测教学成效，并根据学生的特点来设计相应的教学策略，进一步改进教学。

二、研究方法

（一）测试目的

本测试主要通过一道综合的开放题，检测学生学习了2、5、3倍数特征之后，是否能综合应用“2、5、3倍数特征”来解决问题。主要是想了解学生对“2、5、3倍数特征”的应用能力水平及学生的解题策略和思维水平。试图通过对学生解题思维水平的分析，了解教学成效，进一步提出教学改进建议。

（二）被试对象

选择公办、民办小学四年级的两个班，共59人。该校使用浙教版新思维小学数学教材。测试对象已经学习了2、5倍数特征与3的倍数特征的内容。

（三）测试内容

所用问卷为本人根据《义务教育数学课程标准（2011年版）》关于“2、5、3倍数特征”相关知识与能力要求编制而成。测试具体内容如下。

问题一：在五位数25□4□的方格内填什么数字，才能使它既能被3整除，又能被5整除？

你能写出满足条件的这些数吗？请你写一写这些数。

问题二：刚才解决这个问题你是怎样思考的？请写一写你的思考过程，越详细越好。

（四）测试过程

在学生不知情的情况下，由数学老师组织进行测试。在测试前，没有给学生任何的解题提示，也没有读题，让学生独立解答，测试时间15分钟。学生在解题过程中没有任何的讨论与交流，整个测试过程基本反映了学生独立解答这一整除问题的水平。测试后，笔者对学生的解题情况进行初步的整理，并选择10名学生进行个别访谈。

三、结果分析

（一）从整体上分析，约有40%的学生能正确解答此题，且解题策略灵活多样，思维呈现出较高的有序性

对学生的解题情况进行统计后发现：学生能正确解答这个问题的有24人，占40.7 %；解答错误的有35人，占59.3 %。在正确解答的人数中，有83.3%的学生思维呈现出较高的有序性。解题正确的孩子，所采用的解题策略是多样化的，主要有以下几种策略：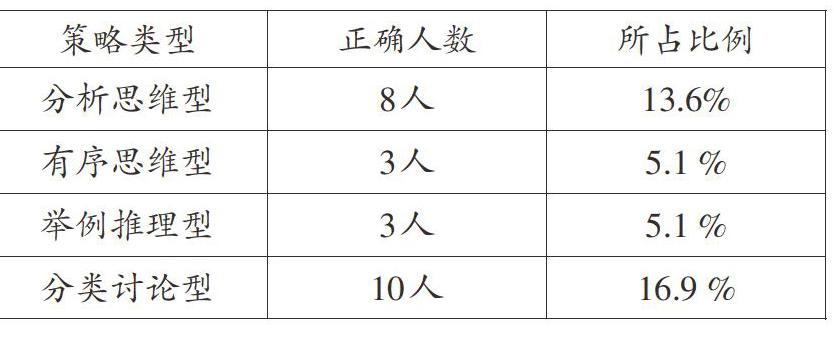

具体分析如下。

1.分析思维型

“分析思维型”是指学生能严格依据“3的倍数特征”与“5的倍数特征”的定义，对问题做出正确的分析。采用这种策略的有8人，占13.6 %。下面是两个学生的解答。

在图1中，学生能分别从“3的倍数特征”和“5的倍数特征”的定义出发，先考虑满足“5的倍数特征”，再考虑能同时满足“3的倍數特征”，有顺序地写出这些五位数。图2也是如此，只不过在分析满足“3的倍数特征”的思维过程中，是用算式去表达的。

2.有序思维型

“有序思维型”是指先确定某个数能同时被3和5整除，再选择其中的一个数位进行变换，依次增加3，使得各数位上的数字之和始终是3的倍数。采用这一策略的有3人，占5.1%。下面是两个学生的解答。

在图3中，学生先确定满足“5的倍数特征”，然后思考如何满足“3的倍数特征”。学生是通过先确定百位上的数可填1，再在这个基础上，依次增加3，使得各数位上的数字之和仍是3的倍数。图4也是如此，只不过学生对思考过程的语言描述不够规范，如“先把另外的数加起来，再加上一个数，使和能被3整除，其他把加上的那个数顺序加3”。其实这两个学生的思维过程基本一致，都是根据改变其中一个数位上的数，进行逐个递增的方法来思考的。

3.举例推理型

“举例推理型”是指学生在说明原理的基础上，进行举例推理，起到归纳概括的作用。采用该策略的有3人，占5.1 %。下面是一个学生的解答。

在图5中，学生能有序地写出所有满足条件的五位数。由定义出发陈述理由，并举例：2+5+4+0=11，要使和能被3整除，应该为12，又因为12-11=1，所以百位应该是1。同理，其他数位上的数也是如此。

4.分类讨论型

“分类讨论型”是指学生能够对问题进行合理的分类讨论。该方法思维严谨，条理清晰，值得推广。采用该策略的有10人，占16.9 %。下面是两个学生的解答。

以上两个学生的解题思路基本一致，都是先确定能被5整除的数的特征，也就是要先确定个位，分别有两种情况：个位填5或0；再进行分类讨论，如果个位是0，那么百位就有3种填法，分别是1，4，7；如果个位是5，那么百位也有3种填法，分别是2，5，8，共6种。采用这一策略的学生思维灵活并严谨。这一方法值得推广。

（二）从错误作品上分析，学生对“2、3、5倍数特征”的理解呈现出水平差异

通过对学生测试题的分析，笔者发现学生的错误解题思维多样化，学生在解决上述测试题时，主要有以下几种典型错误：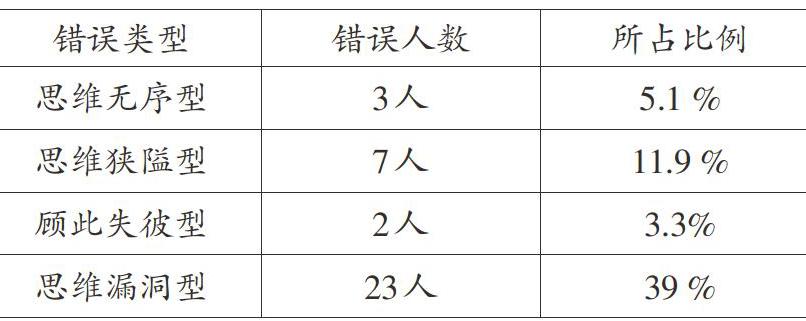

1.思维无序型

“思维无序型”是指思考问题思维混乱，理由离谱。出现这样错误的有3人，占5.1%。下面是一个学生的解答。

该生认为写出来的五位数必须是每个数位上的数字之和等于7或是7的倍数。而他写的数中，每个数位上的数字之和却不全是等于7或是7的倍数，而为什么会认为和7有关呢？这一问题在访谈中了解到，该生认为能被3整除的数只要末位能被3整除就行，而对于自己写的答案却说不出任何理由。显然，这个学生对3的倍数特征不理解，那么关于“3、5倍数特征的应用问题”就更不用说了，已超过他的认知水平。

2.思维狭隘型

“思维狭隘型”是指思考问题只从一个方面出发，不能多角度的思考。出现这样错误的有7人，占11.9 %。

下面是两个学生的解答。

以上两个学生的解答是错误的，但似乎错的有理由。在图9中，学生对3、5倍数特征都是了解的，也能根据特征来写数。但学生思考问题的方向是单一的、狭隘的。如单纯考虑能被3整除的数的特征，写出25041、25044；再如单纯考虑能被5整除的数的特征，写出25145、25240、25345。从学生思考过程的描述中来看，没有将既能被3整除又能被5整除的数的特征相结合，要同时满足两个条件，但学生却忽略了。同样，在图10中，我们发现学生写出来的数只满足5的倍数特征，从思维过程的描述中学生提到“前面的数则没有要求”，完全忽略3的倍数特征，更不要说将两者结合起来考虑了。

3.顾此失彼型

“顾此失彼型”是指思考问题能从不同的角度出发，但对问题做出最终的决策与判断时，又因为顾了这一头，而忘了那一头，不能综合考虑问题。出现这样错误的有2人，占3.3%。下面是一位学生的解答。

在图11中，学生写对了两个数，但在思考问题的逻辑上出现错误。学生先把五位数25（）4（）中的万位上、千位上及十位上的数相加，如：2+5+4=11，再在百位上填上4，认为只要将所有数位上的数相加之和是3的倍数就行，最后一位个位上填0或5。通过访谈得知详细思考过程如下：

该生的错误比较特殊，他对概念的理解是清晰的，知道既要被3整除的数的特征（要看各个数位上的数字之和），又要被5整除的数的特征（要看个位是否为0或5），对知识本身的理解是没有问题的；但在综合思考的时候，没有从个位先入手，只把除个位外的其余四个数位上的数相加作为判断依据，然后再判断个位出现的0和5的两种情况。

4.思维漏洞型

“思维漏洞型”是指思考问题能从不同的角度出发，能写出符合条件的不同的五位数，思考方法是对的，但会有遗漏。出现这样错误的有23人，占39%。下面是两个学生的解答。

在圖12中，学生能先从个位开始考虑，个位是0的情况下，写出了又要同时满足3的倍数特征的数25140、25440和25740；然后再考虑个位是5的情况，但学生却只写出了25245这一个数，有遗漏，考虑不全。在图13中，学生却只写出了个位是5的情况下的满足条件的三个数：25245、25545和25845。而个位是0的情况下却没去考虑。

四、建议与思考

针对本次测试的结果，笔者对教学改进提出如下建议。

（一）关注学生思维能力的水平差异和类型差异，实施差异教学

苏联的克鲁切茨基认为，数学能力差异可分为类型差异和水平差异。数学能力的类型差异又可分为以下三类：分析型（倾向以言语——逻辑的关系来思考）、几何型（倾向以视觉——形象的关系来思考）、调和型（兼具前两种类型的特征）。那么在上述该问题中，如图6（分类讨论型），这类学生属于分析型，他的语言逻辑成分占明显的优势，他习惯用严谨的语言去描述。而错误思维“顾此失彼型”（如图11）这一类型的孩子恰恰属于几何型。这类孩子具有非常好的视觉形象成分，习惯于形象地解释抽象的数量关系。在访谈中，我们可以看到他思维的独创性。他们总是坚持用视觉的图示、表象和具体的概念进行运算（这里用加法算式去表征）。在图5中，“举例推理型”的思维类型所表现的数学能力则更趋向于“调和型”。大多数能力强的孩子都属于这种类型，他们的特征是在语言逻辑成分的主导作用下，保持语言逻辑成分和视觉形象成分的平衡发展。在图5中，我们能看到该孩子逻辑表达能力强，而且会根据所表达的内容进行列举，并推理概括。

数学能力的类型差异是没有好坏之分的。在教学设计时，我们一线教师要兼顾这三种类型差异的学生，在课堂实践中，要创设机会，让学生充分地进行解题表征，让更多的解题图示都得以展示，促进不同类型学生的发展，创设适合的教育，让不同类型的学生都能获得不同的发展。

而学生的数学能力水平差异是有好坏之分的，思维也有高低之分的。在教學实践中，我们可以实施分层教学，也就是差异教学。如教师可以设计智慧A、B、C、D卡。（A卡层次最高，D卡层次最低）每一张卡上都有对2、5倍数特征的一些问题，也是一些提示。并明确告诉学生，如果A卡中你不能完成所有的题，你就需要看B卡或C卡，依次类推。智慧卡如下图：

利用智慧卡，能满足不同思维层次学生的需求，让不同的学生思维得以发展，创设不同的问题情境，让不同的学生获得不同的发展。

（二）针对学生解题的思想方法错误，渗透“分类讨论”思想

学生在用“2、5、3倍数特征”解决问题时，出现了几种思维类型错误。如思维无序型、思维狭隘型、顾此失彼型、思维漏洞型等，占总人数的59.3%。通过错例分析，大部分学生不能灵活运用分类讨论思想方法，思考问题无序混乱。该研究启示我们：在数学教学中，渗透分类讨论、有序思考的思想十分重要。所谓分类讨论思想是指：面对比较复杂的问题，有时无法通过统一研究或者整体研究解决，需要把研究的对象按照一定的标准进行分类并逐类进行讨论，再把每一类的结论综合，使问题得到解决。其实质是把问题“分而治之、各个突破、综合归纳”。而有序思维是指思考和解决问题时遵循一定的顺序、按照特定的线索和步骤去探索的一种思维方式。渗透“分类讨论”思想，培养“有序思维”，可以优化学生思维品质，提高问题解决能力。可以从以下途径开展。

其一，有序观察，有序思考。在数学课堂教学中，教师需引导学生有序观察，使学生进行有条理的思考，达到言之有序、思之有路的目的。例如图3，可以引导学生观察：如果被5整除，个位可以是0，其他数位上的数字之和：2+5+4=11，12-11=1，所以百位可以是1。紧紧抓住被3整除的特性：各个数位上的数之和是3的倍数。于是可以有序累加，1+3=4，百位可以是4；4+3=7，百位可以是7。同样个位换成5，也可以引导学生这样有序思考。

其二，合理分类，有序思考。小学生的思维处于无序思维向有序思维的过渡阶段。重视学生获取知识的思维过程，合理分类，就是引导学生有序思维。例如在归纳能被2整除的数的特征时，可以让学生分类思考，先思考个位都是2的两位数、三位数、四位数，是否能被2整除；再思考个位是4、6、8等数是否都能被2整除，从而推导出2的倍数特征。

其三，有序操作，有序思考。操作是思维的基础和源泉，学生的操作过程，其实就是他思考的过程。例如在教学2的倍数特征时，引导学生经历猜想、操作再到验证的过程，理解2的倍数特征：给出像18，22，36这样的数，利用实物图请学生先猜测如果2个2个分，是否刚好分完。然后通过实际操作验证猜测。接着让学生进一步猜测当5个5个分时，刚好分完，物体的个数应该是几，这些数的个位有什么特点。

（三）加强对比，理清2、5、3倍数特征关系；在综合性问题解决中实现知识求联

学生对概念的理解到应用是有一个过程的。在教学过程中应重视实际应用能力的培养。概念的理解到应用实质上是要经历由知识点—知识域—知识体系的求联过程。那么在解决上述这个问题中，学生需要了解并掌握的知识点是“能被5整除的数的特征是个位上的数是0或5”；“能被3整除的数的特征是各个数位上的数字之和能被3整除”。这两个知识点并非孤立的，学生在学2、5倍数特征时，所采用的思考问题的方法是具有共性的，可通性的，都是从个位开始研究，进行判断。而在3的倍数特征的学习中，也会把这种思考问题的方式进行迁移，发现个位是3、6、9的数不一定是3的倍数，于是就会另辟蹊径，一个新的知识点又诞生了，知识点的诞生扩充了知识域。

在教学时，我们要创设更多的综合性问题情境。不仅要关注一个知识点的丰厚，而且要关注知识点与知识点之间的知识链的求联。当要解决既能被3整除而又能被5整除的数时，我们就要把这两个知识点进行求联，要把这一问题放到整个整除的知识体系中去研究。知识链的求联是需要在综合性问题解决中得以实现的。