企业出口规模越大全要素生产率越高吗?
——基于中国出口企业的经验分析
2018-07-16邢志平
邢 志 平
(厦门大学 经济学院, 福建 厦门 361005)
一、问题提出
企业通过出口能够学习外国的管理经验、技术等以提高自身的生产率,这也是多数文献提到的“出口学习效应”。其具体表现在:发展中国家出口企业从发达国家的贸易伙伴那里免费获得产品设计和改善工艺的技术;国外市场更为激烈的竞争以及对产品质量更为严苛的要求,迫使出口企业更加努力地提高自己的生产率;市场规模的扩大给出口企业提供了增加收入的良好时机,但也给它们带来了提高生产效率的压力[1-2]。
关于出口学习效应,有大量的文献对其做了实证检验。一些文献认为存在出口学习效应。Van Biesebroeck运用1992~1996年南非9个国家制造业企业数据,并且在控制了自我选择效应情况下,发现出口企业在从事出口之后生产率增加了25%~28%,这也说明了出口学习效应的存在[3];De Locker运用1994~2000年间斯洛文尼亚的16个制造业产业的企业数据,发现企业一旦开始出口后将变得更有生产率,同时,还发现出口到发达国家的企业较出口到发展中国家企业有更大的生产率效应[4];张杰等利用1999~2003年间所有国有企业及规模以上非国有企业的企业层面微观数据进行经验分析发现,结果稳健地验证了出口通过出口学习效应促进了我国制造业全要素生产率的增长[2]。与上述结论相反,另一些文献认为并没有充足的证据证实出口学习效应存在。国外学者Bernard和Jensen[5-6]、Wagner[7]及Arnold和Hussinger[8]的相关研究均未发现出口企业和非出口企业在生产率增长方面的差异性;国内学者李春顶和尹翔硕实证检验得出了“生产率悖论”,并发现尽管企业规模是影响出口的主要因素,但出口贸易对于企业生产率的影响是不显著的[9]。通过文献梳理,已有的大多数实证类文献基本都在探讨及检验企业是否出口对其生产率的影响。然而,企业出口的规模是十分不同的,那么,出口规模的大小又是如何影响企业生产率的呢?因此,这一问题也就是本文研究的重心所在。
考虑到以中国工业企业数据为样本,使用OLS方法或固定效应模型对企业全要素生产率进行估计时,存在着同时性(simultaneity)问题和选择性偏差(selection biases)问题[10],因此,本文对Levisohn和Petrin[11]所提出方法(以下简称LP方法)进行改进以估计生产率。之所以选择LP方法是因为,Olley和Pakes[9]所提出方法(以下简称OP方法)以企业投资作为生产率的替代变量,然而企业调整投资的行为没有中间投入那么灵活,因此选择企业中间投入作为替代变量要优于选择企业投资作为替代变量[11]。并且,改进后的LP方法同时建立在OP方法和LP方法的基础上,弥补了传统LP方法无法解决选择性偏差问题这一缺陷。
在探讨企业出口规模对生产率的影响时,计量方面存在以下两个问题。首先,出口可能影响企业生产率,而生产率高的企业又会更有动力出口,即可能存在双向因果关系;其次,出口多的企业,多数是规模、研发、地理位置等方面占优的企业,而这些因素也会影响到企业生产率,因此,这就会造成计量方面的混杂偏差(confounding bias)问题。之前的文献在研究企业是否出口对生产率的影响时,为了克服上述两个问题引入了倾向评分匹配法(Propensity Score Matching,PSM),但该方法只适用处理变量为二元的情况(这里的处理变量即是企业是否出口)。因而,为了更好地反映出口规模对企业生产率的影响,本文引入了广义倾向评分匹配方法(Generalized Propensity Score Matching,GPSM)。
本文首先基于改进后的LP方法估计了企业全要素生产率,并按企业是否出口将企业分为两组,并分别计算各组的全要素生产率均值。其次,本文使用GPSM方法,分别分析了企业出口量及出口密集度对全要素生产率的影响。再次,本文按出口密集度大小将出口企业分为加工贸易型与一般贸易型后,分析出口密集度对全要素生产率的抑制作用在加工贸易型企业中是否存在,并对产生这种现象的原因进行了分析。
二、研究模型与研究方法选择
1.LP方法
假定企业生产采用C-D函数形式,取对数后的估计方程变为:lnYit=β0+βllnLit+βklnKit+ωit+εit。其中,ωit代表全要素生产率。如大多数研究一样,在使用最小二乘法及固定效应方法对TFP进行估计时存在着两个问题[12]:内生性(即异质性企业个体的生产率一定程度上决定了企业要素投入)[13]和选择性偏差(企业的生产率将一定程度决定企业进入和退出市场的概率)[14]。为了克服这两个问题,Olley和Pakes提出了使用企业投资量作为生产率的替代变量的OP 方法[5],Levinsohn和Petrin提出了使用中间投入作为生产率的替代变量的LP方法[11]。
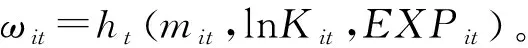
lnYit=βllnLit+φt(mit,lnKit,EXPit)+εit
(1)
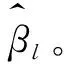
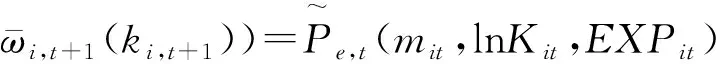
(2)
当企业在t期存在并在下一期续存则表示为χi,t+1=1,相应地存在于t期而在t+1期消失的企业则表示为χi,t+1=0。采用Probit概率计量模型估计,使用二阶多项式逼近,此为估计第二步。
基于企业生产率服从一阶马尔科夫过程的假设,可得:
(3)
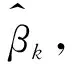
2.GPSM估计模型和方法
Hirano和 Imbens[15]在Rosenbaum和Rubin[16]的基础上将PSM方法中的二元处理变量扩展为连续型,提出了广义倾向评分匹配法(GPSM)。关于PSM方法及GPSM方法的前提假设条件,本文在此不再赘述,具体可参见Becker和Ichino[17]以及Hirano和Imbens[15]。基于之前有关PSM应用的文献[2,18-19],GPSM方法既能够有效解决出口规模变量与企业生产率之间的内生性问题,还能够有效消除出口规模变量与同时影响企业出口和生产率的各类变量之间的混杂偏倚问题。GPSM估计主要分为3步:
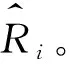
根据Abadie指出的匹配变量的选取规则[21],匹配变量中所包含的变量应为同时影响处理变量和结果变量的变量,即X所包含的变量应为同时影响企业出口规模和企业生产率的变量。因此,本文将X所包含的变量设置如下:①上一期的生产率水平lTFP;②企业规模变量lnl,用企业从业人数的对数值表示;③企业是否位于东部地区的虚拟变量region,其中region=1表示企业位于东部沿海11省份(北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南),其他省份,region=0;④企业是否研发的虚拟变量DRD,其中,DRD=1表示企业存在研发支出,DRD=0表示企业没有研发支出。
三、数据说明及描述性统计
本文所用数据来自中国工业企业数据库,数据时间跨度为2005~2007年。参照聂辉华等[22]、谢千里等[23]的方法,对不合理数据进行了筛选,剔除了那些不符合现实的企业样本,如从业人数少于8人的样本,以及不符合会计准则,如总资产小于固定资产净值、累计折旧小于当期折旧、主营收入大于营业收入、工业增加值或中间投入大于总产出的样本企业。本文使用各省出厂价格指数、固定资产投资价格指数、全国工业原材料燃料和动力购进价格指数对工业增加值、固定资产净值、中间投入进行了平减,数据来源于历年《中国统计年鉴》。同时,用企业从业人数衡量企业的劳动投入。

表1 出口企业与非出口企业生产率均值比较
注:***、**和*分别表示1%、5%和10%的显著性水平。
通过表1,我们看到,在本文统计范围内的所有行业中,出口企业的生产率均值均大于非出口企业,并不表现出“生产率悖论”的特点[24-26]。本文所得结论与范剑勇和冯猛[27]所得结论是相一致的。他们利用要素投入的流量与存量法以及OP、LP生产率估计法,更加细致地比较了出口与内销企业之间的生产率差异,发现出口企业生产率总体上要高于非出口企业。而究其差异的原因,主要在于生产率估计的准确性,反思李春顶[25]在得出“生产率悖论”这一结论时所采用的生产率估计方法,可以看到其所度量的生产率更多是劳动生产率,而在我国出口企业更多是加工贸易型企业的背景下,此类出口企业更多利用了我国廉价劳动的优势,也就是意味着利用更多的劳动替代资本,如果利用劳动生产率去衡量全要素生产率时,将低估出口企业的生产率。因此可以说,企业生产率估计方法的准确性将影响到结论的准确性。本文进一步发展LP方法,将OP方法对样本选择问题的处理引入到LP方法中,以使得生产率估计相比于前期文献更为准确,本文的结论也将更为可靠。
本文删掉出口小于或等于零的样本,仅留下存在出口的企业,以此来分析“出口规模的大小对企业生产率的影响”。首先选择企业出口量这一绝对变量来衡量企业出口规模,经计算可得,企业出口量EX的均值为80 100.28,最大值为1.81e+08,最小值为1。并且其偏度为100.2581,峰度为17 090.08。出口量对数化后均值为9.6352,最大值为19.0140,最小值为0。其偏度为-0.3763,峰度为4.6648,分布如图1。
依据出口量对数化后的分布图1,本文在进行GPSM估计时,第1步使用较为一般的正态分布形式,即g(Ti)|Xi~N(F(Xiβ),σ2)。那么,样本企业的广义倾向评分值为:
其中,g(Ti)是处理变量的合理转换函数。
同时,本文构造出口密集度指标exd(出口交货值除以工业销售产值)。可以看到,出口密集度是企业出口规模的相对指标。出口密集度指数的分布见图2。

图1 出口量对数化后的分布图 图2 出口密集度分布图
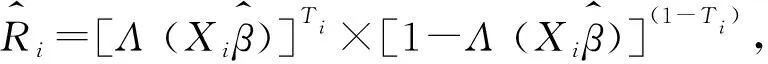
四、GPSM估计与实证分析
根据上文所述,GPSM估计分为3个步骤:第1步的主要目的在于获得样本企业的广义倾向评分值;第2步在于获得下一步估计所需的估计系数;第3步依据前两步的结果获得不同企业出口量或出口密集度所对应的企业生产率水平,此步也是我们最为关心的结果。GPSM估计第1步回归结果见表2。
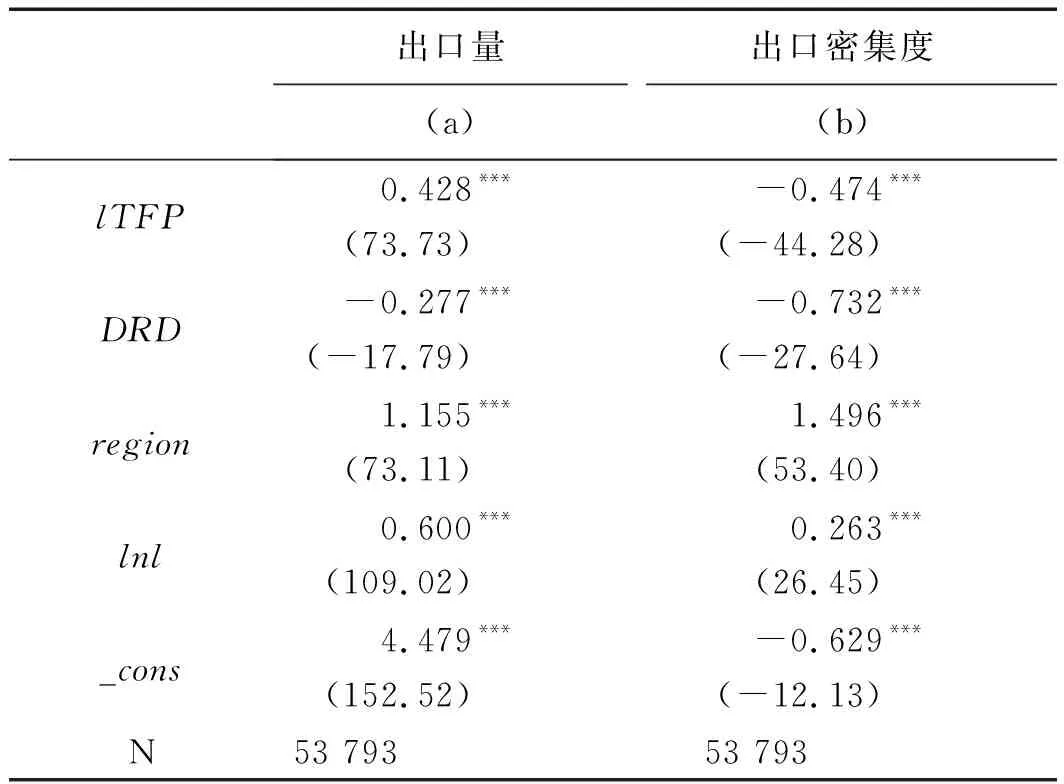
表2 GPSM估计第1步估计结果
注:括号内为回归系数的p值,***、**和*分别表示1%、5%和10%的显著性水平,下同。
通过表2,我们看到,随企业上年生产率的增加,企业出口量逐渐增加,而企业出口密集度逐渐减小。这主要是因为,随企业生产率的增加,企业的产值会加大,企业因而也会增加出口量,然而,企业会把生产的产品更多地销售到国内市场,因而企业出口密集度逐渐减小。企业从业人员越多,企业规模越大,企业出口量及出口密集度也会越大。并且,位于东部地区的企业的出口量及出口密集度都要大于非东部地区。
根据表2得到的回归结果以及各自的条件分布,计算得到了各自的广义倾向评分。其中,出口量广义倾向评分的最大值为0.319 820 7,最小值为1.08e-14,均值为0.241 938 2。出口密集度的广义倾向评分的最大值为0.998 604 1,最小值为0.037 928 2,均值为 0.578 267 7。
GPSM估计的第2步估计结果见表3。其中lnEX代表出口量的对数值;exd代表出口密集度;lnEX2代表出口量对数值的平方项;exd2代表出口密集度的平方项;RlnEX代表出口量对数值的广义倾向评分值;Rexd代表出口密集度的广义倾向评分值;RlnEX2及Rexd2代表广义倾向评分值的平方;lnEXR代表出口量对数值与其广义倾向评分的交互项;exdR代表出口密集度与其广义倾向评分的交互项。
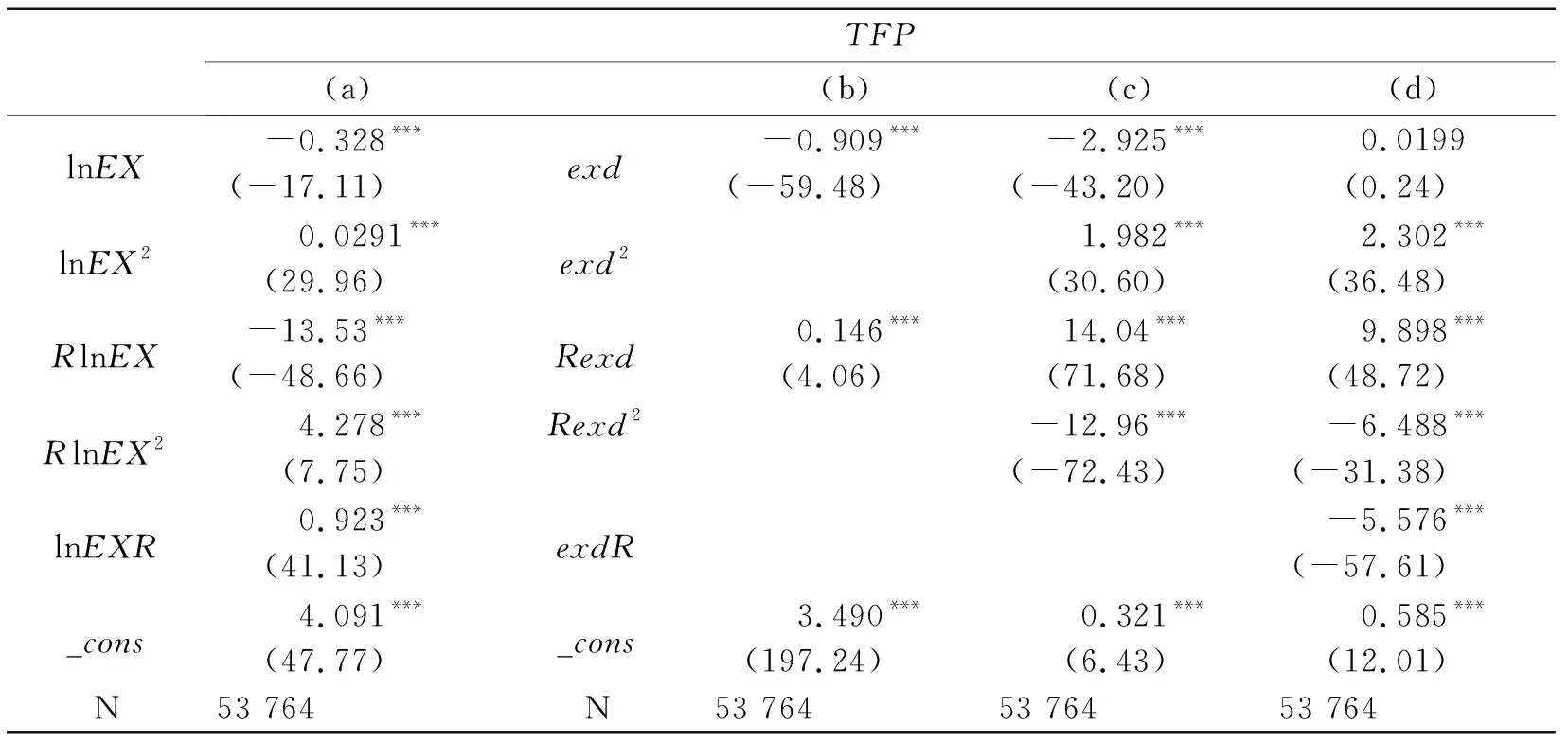
表3 GPSM估计的第2步估计结果
通过表3的估计结果可以看到,(a)列中所有自变量的系数都非常的显著。然而(d)列中exd变量的系数并不显著,因此,本文采用逐步回归法。基于本文的研究的目的,首先对exd及Rexd两个变量回归可以看到系数非常显著,然后逐步加入二者的平方项,系数仍然显著,并且可以看到exd及Rexd的系数的正负并不发生变化,然而当加入二者的交互项后,exd的系数变得不显著且系数的正负性发生变化,因此,本文采用(c)列的结果。
基于第2步的估计结果,我们可以得到出口量及出口密集度对生产率的因果效应散点图如图3、图4所示。
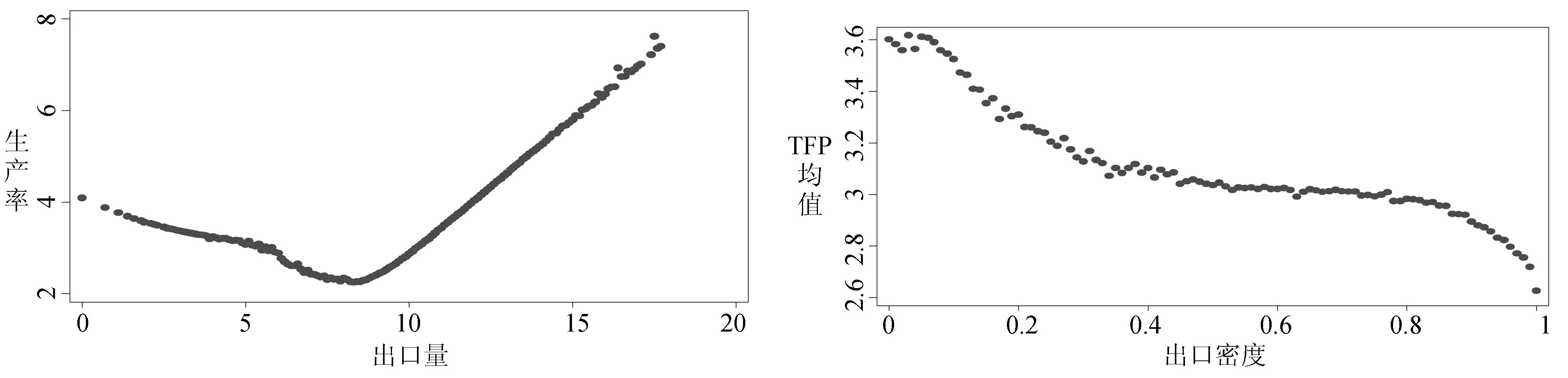
图3 出口量对生产率的因果效应 图4 出口密度对生产率的因果效应
通过图3可以看到,随出口量的增加企业生产率逐渐减小,而后到达一定数值后,即出口量的对数值为7.8时,随出口量的增加,企业生产率逐渐增加,出口量对企业生产率呈现出先抑制后促进的作用。本文通过计算发现,出口量对数值小于7.8的企业仅为9201家,而出口量大于零的企业有72 736家,也就是说,出口量对数值小于7.8的企业数量仅占总体的12.6%,因此,鉴于如此小的企业数量,总体上可以认为企业出口量对生产率具有正向的促进作用。相对于之前检验“出口学习效应”的文献,本文不仅仅分析了企业是否出口对企业生产率的影响,而且分析了企业出口多少对企业生产率的作用。这也进一步验证了企业的“出口学习效应”。
通过图4可以看到,随出口密集度的增大,企业生产率逐渐减小,企业出口密集度对企业生产率存在着抑制作用。根据之前相关文献的解释,之所以出现图4所示的现象,与出口企业的贸易类型不同有密切关系[28-29]。本文将出口企业主要分为两类,一类是一般贸易型企业,另一类是加工贸易型企业。由于本文使用的数据库中没有加工贸易类型这一统计项目,无法直接得到企业出口类型,然而,加工贸易型企业的主要特征是最终产品大多数用于出口。因此,本文借鉴李春顶[25]的做法,将企业出口密集度大于50%的企业定义为加工贸易型企业。经过测算,60%的出口企业都属于加工贸易型企业。对于加工贸易型企业,该类企业主要是利用中国廉价的劳动力资源,承接发达国家企业外包出来的产品价值链中低技术劳动密集型工序[29]。并且,该类企业的技术、管理基本上依靠从外方授权获得[30],然而,外方企业会严格控制技术转移,使得中方加工贸易企业的技术水平提升基本处于停滞状态。这也说明我国加工贸易企业的出口密集度越高,意味着对外方企业的依赖程度也越高。因而最终表现出,我国企业出口密集度对企业生产率呈现反向抑制作用。
为了进一步找出图4所示现象的原因,本文将出口企业分为一般贸易型及加工贸易型两组,并分别估计了出口密集度对企业生产率的影响。最终结果如图5、图6所示。
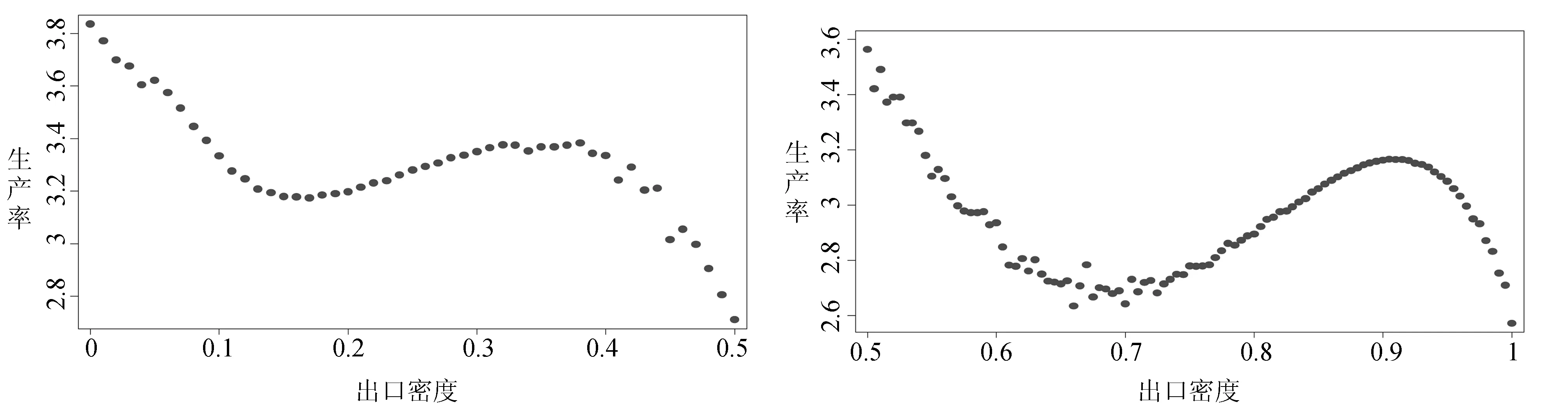
图5 一般贸易企业出口密度对生产率的因果效应 图6 加工贸易型企业出口密集度对生产率的因果效应
通过对各个区间段企业数量的测算,在图5中,出口密集度位于[0,0.17]区间的企业数量占一般贸易型企业总量的58.4%;位于[0.17,0.37]区间的企业数量占比为27.5%;位于[0.37,0.5]区间的企业数量占比为14.1%。可以看到,一般贸易型企业中多数企业位于生产率随出口密集度下降的区间段。因此可以看出,出口密集度对生产率的反向抑制作用不能仅仅归结为加工贸易型企业所存在的问题,一般贸易型企业也存在着出口密集度对生产率的提升具有抑制作用这一现状。本文通过对出口密集度与企业研发强度(研究开发费/产品销售收入)作相关分析,得到两者的pearson相关系数为-0.0373,同时p值为0.000,可以看到,出口密集度越大的企业其企业研发强度反而越小,这也就意味着,一般贸易型出口企业存在着显著的研发“惰性”现象。随着出口企业出口密集度的增大,出口企业的研发“惰性”增大,而导致企业生产率逐步减小[28-29]。并且,由于我国出口导向政策使得政府对出口企业的限制较为宽松,对出口企业也存在着一系列优惠政策,使得出口企业提高自己生产率的动力不足。在图6中,出口密集度位于[0.5,0.72]区间的企业数量占加工贸易型企业总量的16.7%;位于[0.72,0.9]区间的企业数量占比为16.8%;位于[0.9,1]区间的企业数量占比为66.5%。可以看到,加工贸易型企业中,大多数企业都位于生产率随出口密集度增大而下降的区间段,也就是说,出口密集度对企业生产率的提升确实存在着明显的抑制作用。
基于以上分析,出口带来企业生产率提高的原因在于“出口学习效应”,并且出口学习效应也将随着企业出口绝对量的增加而增强。如果企业出口绝对量越多,那么该企业将对国外企业或国外环境更加亲近和了解,相反,更深入亲近和了解也将从绝对量上更多更深地影响到出口企业,使其加深对国外的先进技术或是管理经验的了解和学习,国外激烈的竞争和严苛程度也将更多地从绝对量上影响出口企业(本文通过对出口量与企业研发投入量作相关分析,得到两者的pearson相关系数为0.2695,同时p值为0.000)。然而出口密度则更多地反映了出口企业对出口的相对依赖程度。对于加工贸易型企业来讲,该类企业主要是利用中国廉价的劳动力资源,承接低技术劳动密集型工序部分,技术管理也基本依靠外方,在外方企业技术严格控制下,出口企业更多成了一个无自己技术的加工厂。对于一般贸易型企业来讲,出口密度也同样意味着相对依赖,出口密度越高,相应依赖程度越高,自己进行研发而提高自身技术的激励相应越小,尤其是在一些出口优惠政策的刺激下,自己努力研发的激励就变得更小。最终表现出,企业出口密度越高,企业生产率反而越小的状况。
五、结论与政策建议
综上分析,我们看到:所有制造业行业的出口企业的生产率均值普遍大于非出口企业,企业出口并不表现出“生产率悖论”的特征。并且,随出口量的增加,企业生产率逐渐增高,出口量对企业生产率存在着明显的正向促进作用,这进一步验证了企业的“出口学习效应”。然而,出口密集度对企业生产率存在着反向抑制作用。通过将样本分为一般贸易型和加工贸易型两组,我们看到,出口密集度对生产率的抑制作用不仅在加工贸易型企业中存在,在一般贸易型企业中也存在。
上述分析结论比较全面地描述了企业出口规模对生产率影响的现状,同时,该结论对我国贸易政策改革具有重要的借鉴意义。
第一,出口贸易对提高企业生产率确实存在着一定的促进作用,我国贯彻执行的出口导向政策对帮助提高企业的技术水平和生产率起到了积极作用。并且,随企业出口量的增加,企业生产率也呈现增大的趋势。然而,企业出口密集度对企业生产率却存在着反向作用。因此,出口企业应该在自己做强做大的同时增加自己的出口量,不能仅仅以出口作为自己的目标。
第二,加工贸易型企业对外部依赖程度较大,导致企业生产率随出口密集度的增大而减小。其原因在于,该类企业凭借国内廉价劳动力优势,承接国外外包而来的低技术劳动密集型工序,其技术主要从发包方获得,然而发包企业为保持自己的竞争力会严格控制核心技术的转移,最终导致国内加工企业的技术提升基本处于停滞状态。因此,加工贸易型企业应该积极挖掘自己的核心竞争力,努力走出自己的一条创新道路,而不是仅仅依靠外国企业低技术含量业务的外包。随着中国劳动力成本的升值,外国企业必然逐步将外包业务转移出中国,如果加工贸易型企业对外部依赖程度仍然较大,那么很有可能会面临关闭的风险。
第三,一般贸易型企业也面临着企业生产率随出口密集度增大而减小的问题。究其原因,本文认为,一般贸易型企业的技术进步更喜欢依赖于从国外模仿、学习,而依靠自主研发的程度较弱,并且随着企业出口密集度的增大,出口企业的研发“惰性”会进一步强化。同时,由于政府对出口企业的各项优惠政策,导致出口企业提高生产率的动力减弱。因而政府应该积极鼓励出口企业加大自己的研发投入,并逐步退出各项优惠政策,以此倒逼出口企业努力提高自身生产率及竞争力。
