基于阵列天线结构优化的自适应抗干扰技术

项建弘，李高原，许庆帅

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

0　引言

得益于卫星独特的广域和高度优势，卫星导航系统已经成为高精度、全天候、全球导航定位应用最为广泛的导航系统。然而卫星导航信号到达地面时极其微弱，很容易受到有意或无意的干扰，所以研究卫星导航抗干扰技术具有重要意义。在卫星导航抗干扰中，传统自适应波束形成算法在干扰方向形成零陷，从而抑制干扰。然而信源与干扰源时域相关、空域相邻时，传统自适应波束形成算法会导致波束畸变，期望信号会被抑制造成检测不理想。针对上述问题，均匀阵列通常需要增加阵元数和通道数，以获得更大的阵列孔径，提高分辨率。随着现代技术的发展，天线阵元成本降低，接收机成本受通道数影响较大，主要集中在射频模块、下变频模块以及数模转换模块[1-2]。而且通道数增多，同时会增大通道失配带来的影响。在通道数受限的条件下，阵元位置即阵列天线结构，成为影响阵列自适应波束形成抑制干扰性能的重要因素[3]。

自适应阵列的抗干扰性能不仅仅取决于自适应抗干扰算法的优化，同时还取决于抗干扰模块前端的自适应阵列结构上的优化。由H.Van Trees[4]的最优阵列处理一书可知，天线阵元之间的相对间距和相对位置在天线设计阶段就已经完成，阵列间距和位置一旦确定，阵列流型便固定了，阵列的自由度不高，一定程度下会导致固定结构阵列在某些干扰角度上的自适应抗干扰性能不如结构灵活可变的阵列。1982年，H.C.LIN[5]提出了空间相关系数的概念，并结合阵列结构和空间相关系数，提出了影响自适应阵列性能的因素；1992年，苗振江[6]提出了通过合理设计阵列能够使自适应阵列具有最优的抗干扰效果的观点；2014年，王向荣[7]提出了阵列可重构的思想。结合上述分析，通过引入空间相关系数评价，提出了基于平面阵转向的自适应抗干扰技术。通过阵列天线结构优化，优化期望信号与干扰信号的空间相关系数，控制平面阵最佳转向，克服期望信号与干扰信号空域相邻时在固定阵列上相关程度高导致性能严重下降的不足，提高输出信干噪比，增强导航的抗干扰能力。

1　自适应波束形成技术的基本原理

阵列是由一系列阵元根据相应的形状排列组合而成，其结构如图1所示[8]。主要以拥有M个阵元、阵元间距d为半波长的均匀线阵为基本数学模型结构，且定义入射信号方向与天线阵列的法线夹角为θ。

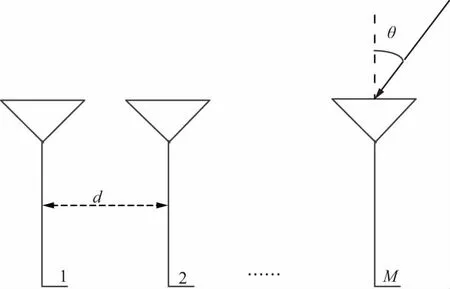
图1　均匀线阵的结构

将1阵元作为参考阵元，令τm为其他阵元与参考阵元收到相同信号的相对时延，其中m∈[1，2，···，M]，则τm可表示为：

(1)

由式(1)可得该阵列的方向矢量为：

(2)

由式(2)可以看出，在阵列结构和接收信号波长一定的条件下，阵列的方向矢量只与图1中的空间角θ有关，与其他元素无关。所以，可以用a(θ)来表示均匀线阵的方向矢量。除此之外，方向矢量与参考阵列的选择也无关。若信号源的数量为D，其方向矢量可分别用a(θi)(i=1，2，...，D)表示，因此可得出方向矢量矩阵为：

(3)

输出的阵列向量可以表示为：

(4)

其向量表达式为：

y(n)=wTx(n)，

(5)

式中，w(θ)=[w1(θ)，w2(θ)，...，wM(θ)]T表示权矢量。

2　基于平面阵转向的自适应抗干扰技术

2.1　空间相关系数理论研究

阵列天线是通过调整每个阵元的权重来将其主波束对准期望方向的，零陷对准干扰方向，实质上调整权值的过程也是变相地调整阵元的位置[9]。用空间相关系数表示期望信号与干扰信号在阵列上所体现的空间相关程度，则空间相关系数的推导过程如下:实验设置N个阵元阵列，期望信号和干扰信号的俯仰角和方位角信息，分别为(θs,φs),(θj,φj)。根据基础知识易得，俯仰角和方位角信息可以定义为：

us=[sinθscosφssinθssinφs]T，

(6)

uj=[sinθjcosφjsinθjsinφj]T。

(7)

Vs和Vj分别为期望信号和干扰信号的导向矢量，且不考虑极化矢量，

(8)

(9)

式中，P=[P1，P2，…PN]T∈RN×2包含了阵元的位置信息。即阵元的位置信息定义为：

(10)

假设各阵元的噪声相互独立且与信号独立，卫星导航信号功率远远小于干扰信号功率，易得出对应自适应阵列的协方差矩阵为：

(11)

(12)

式中，σ2为每个通道的热噪声功率；Ps为期望卫星导航信号的功率；Pj为干扰信号功率。

由式(12)可知干扰和噪声的协方差矩阵，应用经典矩阵求逆公式[10]，求逆公式为：

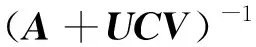
(13)

在单干扰情况下，式(12)可以写成：

(14)

应用SMW矩阵求逆公式可得：

(15)

定义空间相关系数：

(16)

由式(16)易得|αjs|≤1，这个参数被定义称为空间相关系数，它表征期望信号和干扰信号在阵列上的空间分离程度(相关程度)。

由此结合式(15)得到：

(17)

通常阵列输出的信干噪比(SINRout)[11]定义成式(18)的形式：

(18)

结合式(15)可得：

(19)

式中，Ps表示期望信号功率；SNR=Ps/σ2；

(20)

ρ描述干扰和噪声功率的比值，由式(19)可知，0≤ρ<1；当干扰相对于噪声功率较小时，ρ接近于0，噪声对输出信干噪比影响较大；当干扰相对于噪声功率较大时，ρ接近于1，干扰对输出信干噪比性能影响较大。

上述分析可知，输出信干噪比是空间相关函数的减函数，且在干噪比较大的情况下，输出信干噪比受空间相关系数影响明显。由此可知，在已知阵列的阵形下，只需要知道期望信号和干扰信号，就可以计算出期望信号与干扰信号的空间相关系数，阵列的输出信干噪比就可以计算出来。反过来，只要知道期望信号和干扰信号，就可以通过期望信号和干扰信号的空间相关系数来设计优化阵列阵形，提高卫星导航系统的有效捕获性能及其抗干扰能力。

在自适应阵列抗干扰处理中，干扰信号和期望信号的方向信息一旦确定，这个值在理论上是确定的，所以只能通过阵列结构上的优化，来达到减小空间相关系数的目的。本文不考虑阵元的方向函数及阵元的转向，只从阵列结构的角度出发，通过阵列结构的优化配置来改善输出信干噪比，进而在一定程度上提高卫星导航系统的抗干扰能力和有效捕获性能。

对于期望卫星信号的来向信息获取，可以由惯性导航信息和卫星星历获得。对于干扰信号的方位信息获取，可以针对不同的环境利用不同的测向方法获取干扰信号的方位信息。

2.2　基于平面阵转向的自适应抗干扰技术

由文献[12]可知，通过改变阵列天线的转向，能够使得卫星导航信号与干扰信号在阵列上所体现的空间相关系数减小，从而获得更好的输出信干噪比，进而在一定程度上提高卫星导航系统的有效捕获性能和抗干扰能力。

将阵列转向技术由均匀线阵扩展到平面阵，平面阵阵列转向也可以改变空间相关系数，提高输出信干噪比，下面进行平面阵转向技术的研究分析[13]。

假设已知期望卫星导航信号和干扰信号来向为(θs,φs)，(θj,φj)，由式(6)和式(7)可知空间DOA信息为：

s=[sinθscosφssinθssinφs]T，

(21)

j=[sinθjcosφjsinθjsinφj]T。

(22)

定义平面阵位于x-y平面内，平面阵阵元布局如图2所示，阵元的位置坐标可以定义为(xk,yk)(k=1,2,...N)，阵元间距为d(其中d=λ/2)，定义平面阵在平面的旋转角度为φ，阵元的位置信息定义为：

(23)

特殊情况下，均匀矩形阵是平面阵的一种有规则的情形，当平面阵为均匀分布的M×N矩形阵时，P可以改写成：

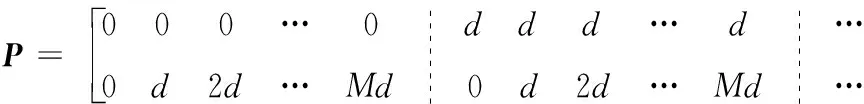
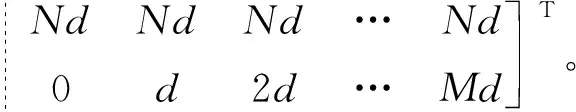
(24)

Vs和Vj分别为期望信号和干扰信号的导向矢量，且不考虑极化矢量，表示如下：

(25)

(26)

则将空间相关系数αjs进行分析有：

(27)

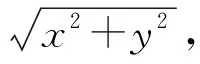
阵元的位置发生变化，由式(27)可知空间相关系数会发生改变。依据上述研究，实验中采用峰值搜索的方法，获得矩阵转向最佳角度φopt，分析转向角度与空间相关系数、输出信干噪比之间的关系，并实验仿真分析转向角度对阵列抗干扰后卫星信号捕获相关峰的影响[14]。

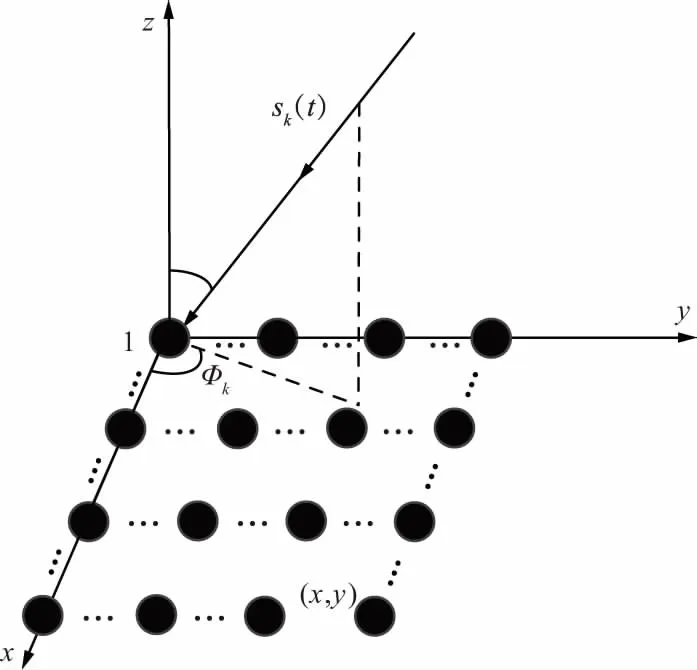
图2　平面阵阵元布局

3　实验仿真结果及分析

本实验以矩形阵为例，研究矩形阵转向φopt与空间相关系数的关系，并得到最佳转向φopt与最次转向φworst。并利用卫星信号捕获相关峰分析最佳转向φopt与最次转向φworst对阵列抗干扰的影响。

在本次实验中采用2行4列的均匀矩形阵，即M=2,N=4阵元数为8的均匀矩形阵，阵元间距为λ/2。设置信噪比SNR=-20 dB，干噪比JNR=70 dB，卫星导航信号的来向方位信息为(θs,φs)=(22°,20°)，干扰信号的来向方位信息为(θj,φj)=(20°,20°)。在仿真分析中设定阵列的旋转配置角度范围为0°～180°，通过仿真实验可得阵列转向角度与空间相关系数的关系曲线如图3所示，同时可得阵列转向角度与归一化的输出信干噪比关系如图4所示。

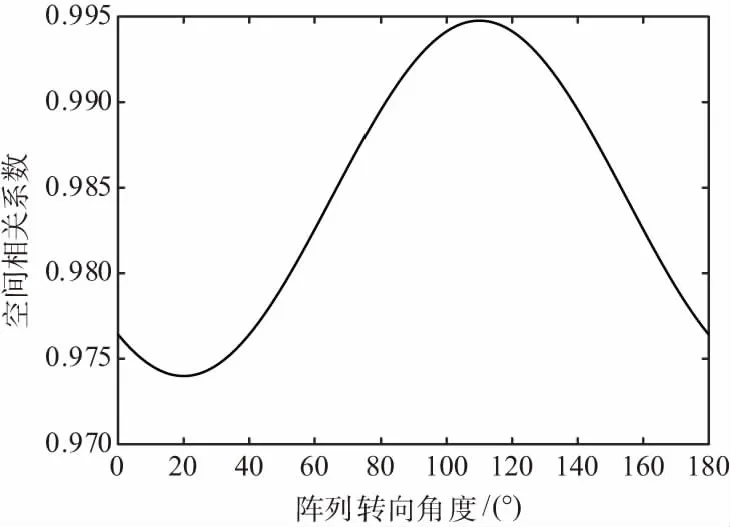
图3　转向角度和空间相关系数的关系

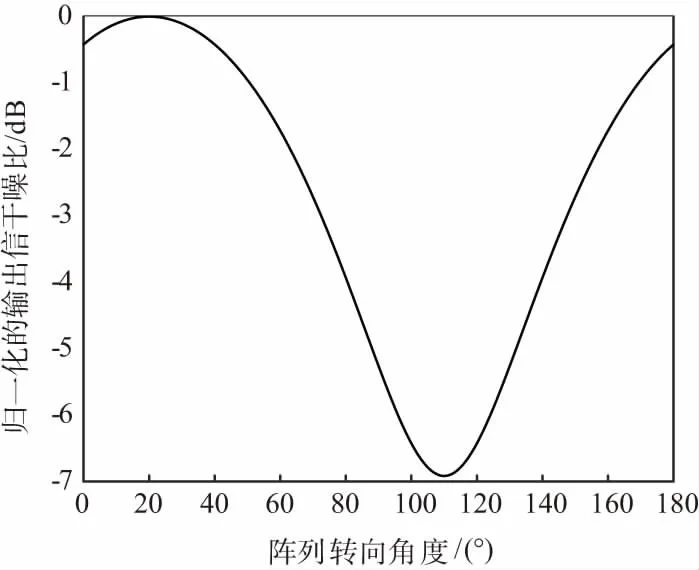
图4　转向角度和输出信干噪比的关系

由图3和图4可知，平面矩形阵阵列转向角度和空间相关系数仍然存在关系，转向角度可以改变空间相关系数。由分析可知在φ=20°左右时，空间相关系数最小，此时输出信干噪比最大；在φ=110°左右时，空间相关系数最大，此时输出信干噪比最小。当φ=110°时，比φ=20°时输出信干噪比提高约7 dB。可知，利用平面阵的最佳转向，优化期望信号与干扰信号的空间相关系数，克服期望信号与干扰信号空域相邻时在固定阵列上相关程度高导致性能严重下降的不足，提高SINRout，提高导航的抗干扰能力。

卫星导航信号到达导航接收机天线，信号经过前端处理，经过抗干扰模块后重新变成中频数字信号，中频信号进入接收机的后续处理模块，进行卫星导航信号的捕获等操作[15]。相关峰(Correlation Peak)[16-17]能够体现卫星导航系统的有效捕获性能，并直接反映了自适应抗干扰的效果。因此在本文均采用卫星信号的捕获相关峰来直观地描述自适应阵列的抗干扰性能。

对均匀矩形阵在不同的阵列转向方向上的卫星导航信号的捕获情况进行仿真分析，为了方便分析，本实验选择转向角度为最佳转向角度φ=20°与最差转向角度φ=110°做对比。设置捕获积分时间为8 ms，实验仿真结果如图5和图6所示。

由图5和图6的对比可知，当平面阵矩形阵转向角度为φ=110°时，相比转向角度为φ=20°时，阵列抗干扰后卫星信号捕获相关峰性能不佳，捕获因子小，即平面矩形阵的最优转向角度的阵列抗干扰后，卫星信号捕获相关峰要比最差转向角度捕获相关峰更理想。平面矩形阵具有类似线阵的转向特性，可以利用平面矩形阵的最佳转向，优化期望信号与干扰信号的空间相关系数，克服期望信号与干扰信号空域相邻时阵列性能严重下降的不足，提高输出信干噪比，提高导航的抗干扰能力。

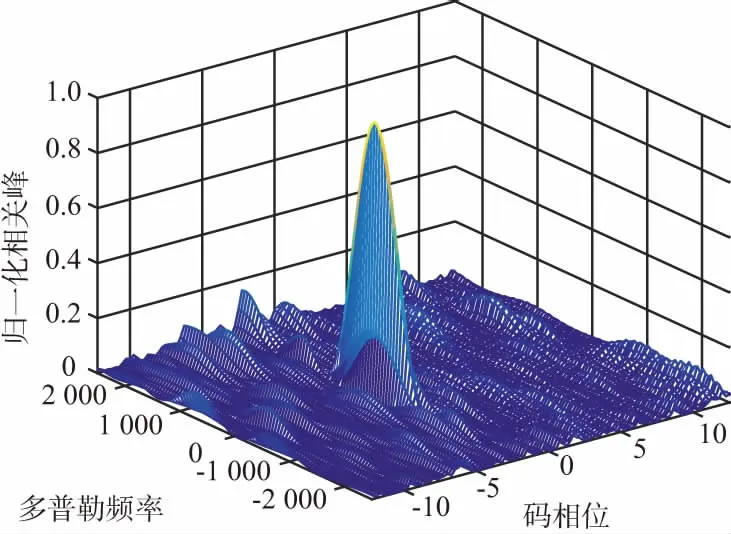
图5　最优转向角度的阵列抗干扰后卫星信号捕获相关峰

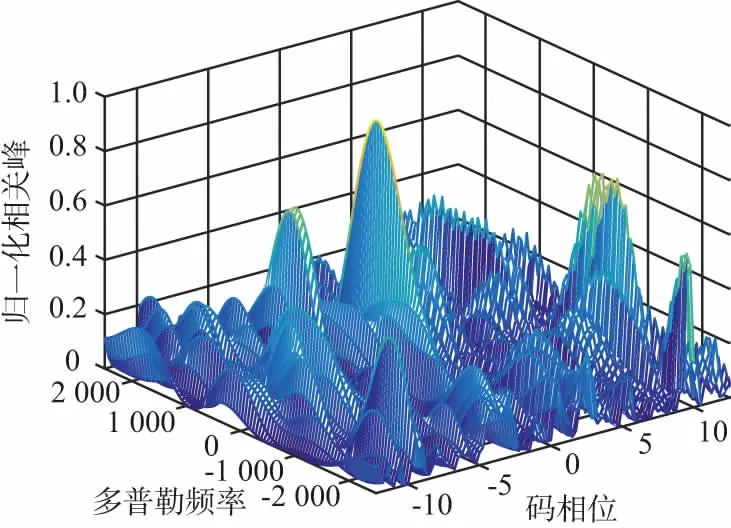
图6　最差转向角度的阵列抗干扰后卫星信号捕获相关峰

4　结束语

复杂电磁环境使得卫星导航系统很容易受到有意或无意的干扰，会导致卫星导航系统性能下降甚至失效，所以提高卫星导航系统的抗干扰能力至关重要。卫星导航系统的抗干扰性能不仅取决于自适应抗干扰算法的优化，而且还取决于抗干扰模块前端自适应阵列天线结构的优化。本文针对信源与干扰源时域相关、空域相邻情形，研究基于阵列结构优化的导航抗干扰技术。

通过引入空间相关系数评价，提出了基于平面阵转向的自适应抗干扰技术。通过改变阵列天线结构，优化期望信号与干扰信号的空间相关系数，控制平面阵最佳转向，克服期望信号与干扰信号空域相邻时在固定阵列上相关程度高导致性能严重下降的不足，提高输出信干噪比，增强导航的抗干扰能力。仿真结果表明，本文提出的基于平面阵转向的自适应抗干扰技术有效。信源与干扰源空域相邻时，平面阵转向技术可以提高阵列的输出信干噪比，增强卫星导航系统的抗干扰能力和有效捕获性能。