山地城市建筑桩基与土质边坡相互作用研究

陈欣韩军

（1.中国十七冶集团有限公司 马鞍山243000；2.重庆大学土木工程学院 400045）

引言

在山地城市的发展建设过程中，由于土地资源紧张，常需要在靠近边坡顶部的位置修筑建筑。这样不可避免地出现一些桩基建在靠近边坡顶的坡体中，这些桩基除了承受结构传来的竖向荷载和水平荷载之外，还将承受来自坡体的侧向土压力，这也导致坡体中的桩基同时具有承重与阻滑的双重功能，边坡对桩的承载力的发挥有一定削弱作用。另一方面，边坡失稳将会威胁到人民生命财产的安全，建筑桩基把上部结构传下来的力传给边坡，对边坡的稳定性也会产生影响。

目前边坡的支挡加固与建筑桩基础的设计还处在相对独立的状态，因此为确保边坡顶面上建筑物和边坡的安全，分析坡体内桩基的受力机理以及桩基对边坡的影响，对桩基以及支挡结构的设计与施工有一定的工程实用价值。

1 计算模型及参数确定

1.1 有限元模型的范围选取

大多数桩土分析问题都涉及无限域或半无限域，而数值分析法是在有限的区域内进行离散化。为了使有限元模拟的结果比较准确，必须取足够大的计算范围。但是如果计算范围过大将会导致单元数过多和计算时间过长。本文模型计算范围的确定参考了郑颖人院士［1］的研究成果：当坡脚到右端边界的距离为坡高的1.5倍，坡顶到左端边界的距离为坡高的2.5倍，且上下边界总高不小于2倍坡高时，计算精度最为理想。本文的土质边坡有限元模型，坡高5m，坡脚到右端边界的距离为20m，坡顶到左端边界的距离为40m，坡体上下边界总高14m，Z向土体的宽度为14m，符合郑颖人院士所指定的计算范围。边坡模型示意如图1所示。

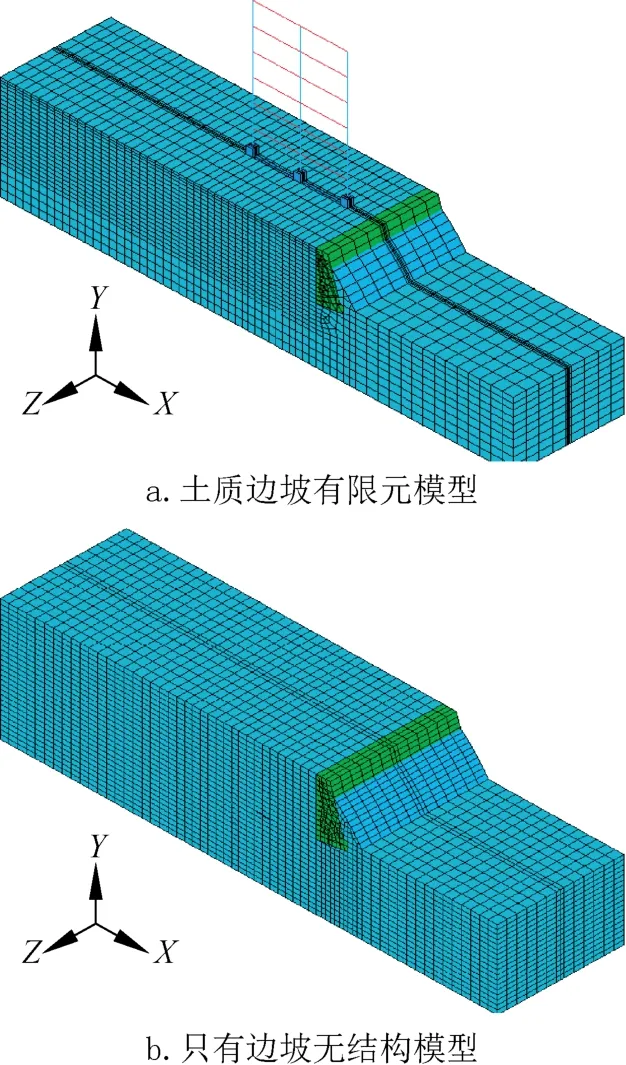
图1 土质边坡基本模型Fig.1 The basic model of soil slope under gravity

1.2 材料属性

梁、柱、桩、挡土墙定义为线弹性材料。土体采用ANSYS中的DP材料模型。

1.3 单元的选择

梁和柱采用三维梁单元beam4；底部的柱、桩、土体、挡土墙等采用20节点的三维实体solid95单元；桩土接触面采用targe170和conta174单元；多点约束单元MPC184单元用于连接梁单元的柱和实体单元的柱，以传递弯矩。

1.4 边界条件

边坡的底部边界为固定边界，设置X，Y，Z三个方向的约束，左右边界设置X方向的约束，前后边界设置Z方向的约束。

2 算例设计

结构-桩-边坡体系分析基本模型如图1所示，其基本参数为：框架跨度为6m，层高3m，梁尺寸为0.3m×0.6m，柱尺寸为0.8m×0.8m；采用均质土，土体X向尺寸为55m，Y向尺寸为14m，Z向尺寸为14m。桩长10m，桩尺寸0.8m×0.8m。坡高5m，切坡前坡率1：1。切坡后设置直立式重力挡土墙，墙顶宽1.5m，高度6m，墙面坡度为1：0.3，墙背直立，基底坡度为1：0.14，墙趾厚度为1m。挡土墙的设计按照挡土墙标准图集［2］选取，材料参数具体取值见表1。

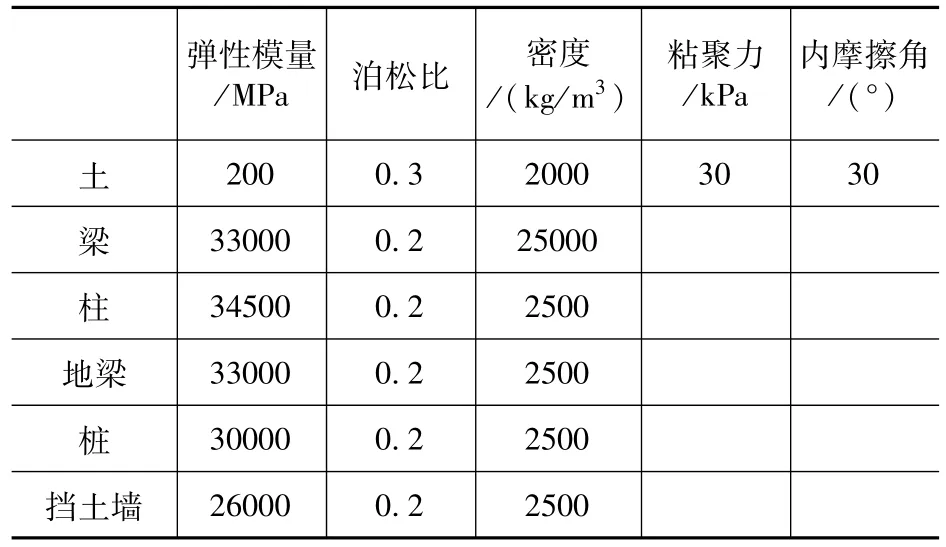
表1 土质边坡材料参数Tab.1 The material parameters of soil slope model

另外，建立了只有边坡无建筑结构的模型，用于与边坡有结构模型进行对比，研究建筑框架和桩基对边坡支挡结构的作用。

3 结果及分析

3.1 建筑桩基对边坡的影响

用有限元折减法对土的抗剪强度进行折减后，边坡出现贯通的塑性区，使土达到极限平衡状态，土压力的分布也出现变化。

试算出无结构模型的安全系数为4.2，等效塑性应变如图2所示，边坡破裂面在45°左右。有结构模型的安全系数为4.05，建筑和建筑荷载减小了边坡的安全系数，边坡仍然出现了贯通塑性区，但是由于有建筑桩基的存在，在桩附近的土没有形成45°左右的贯通破裂面，塑性区主要出现在桩周围以及桩和挡土墙之间。

有结构模型和无结构模型挡土墙上不同高度土压力平均值如图3所示。由图3可知，有结构模型和无结构模型的挡土墙上部1m的土压应力很小，几乎为零，可知它们都为主动土压力。由图4可知，云图应力等值线接近一条条水平的平行线，在中部靠近桩基的部位应力等值线没有出现明显的弯曲。说明当边坡达到极限平衡状态时，建筑桩基传力到边坡的作用很小。

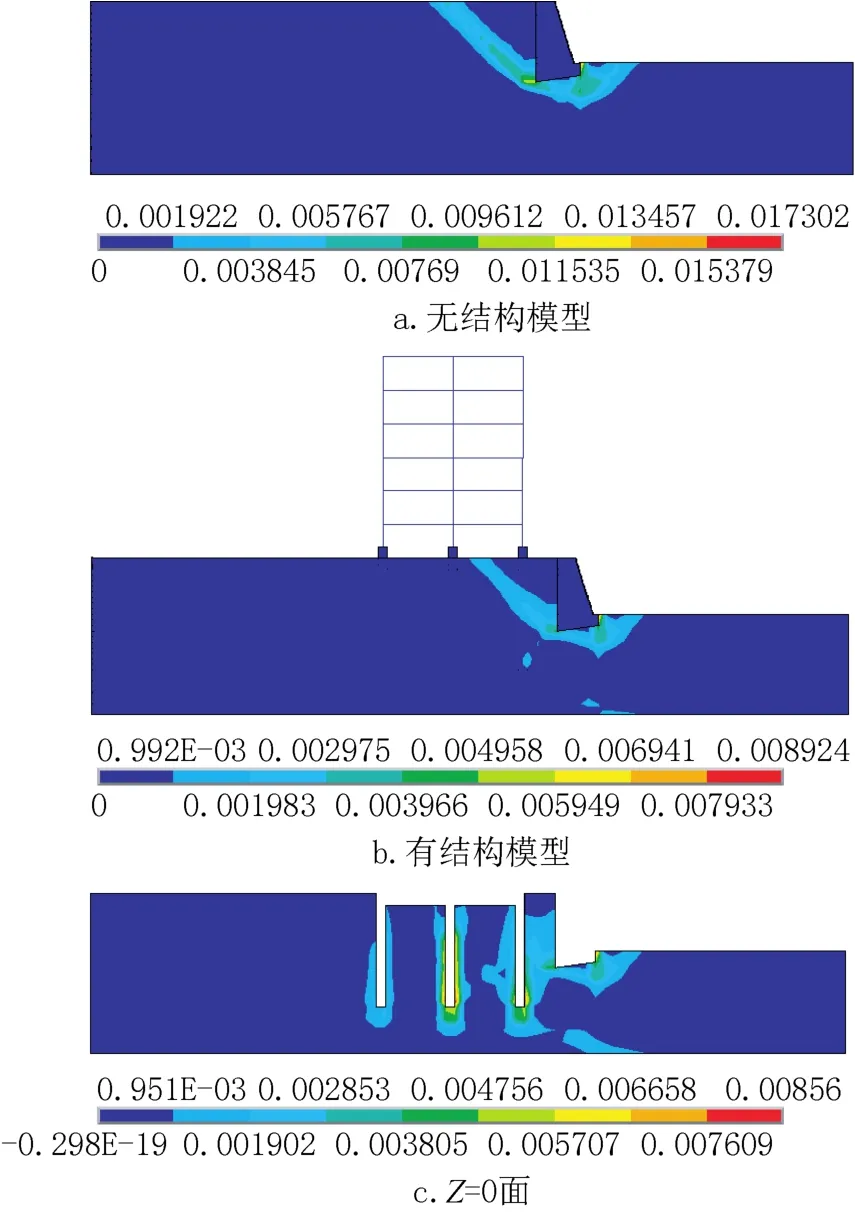
图2 基本模型等效塑性应变云图Fig.2 The equivalent plastic strain contour image of basic model

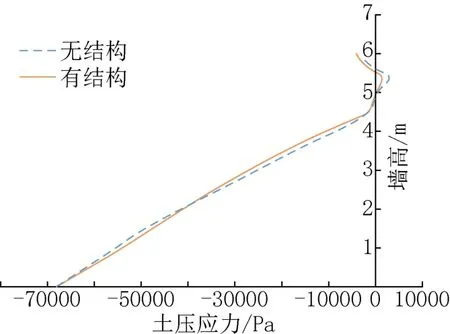
图3 平均土压应力Fig.3 The average earth pressure of retaining wall

图4 有结构模型土压应力云图（单位：Pa）Fig.4 The soil pressure contour image of retaining wall（unit：Pa）

由图5可知，无结构模型挡土墙最大位移为16.47mm，而结构模型的挡土墙最大位移为8.39mm，为无结构模型的50.94%。这说明建筑桩基的存在起到了类似抗滑桩的有利作用，减小了边坡的变形。此时无结构模型挡土墙的位移除以墙高为0.27%。文献［3］中分析出挡墙不同的变位模式时，平动模式所需的挡土墙位移和墙高的比值为Δ/H=0.14% ～0.16%，绕墙底模式所需挡土墙位移和墙高的比值为Δ/H=0.35% ～0.40%，绕墙顶模式所需挡土墙位移和墙高的比值为Δ/H=0.2% ～0.25%。本文的无结构模型极限状态下挡土墙的最大土压力出现在下部，为绕墙顶模式，Δ/H=0.27%，满足主动土压力状态所需的挡土墙位移。

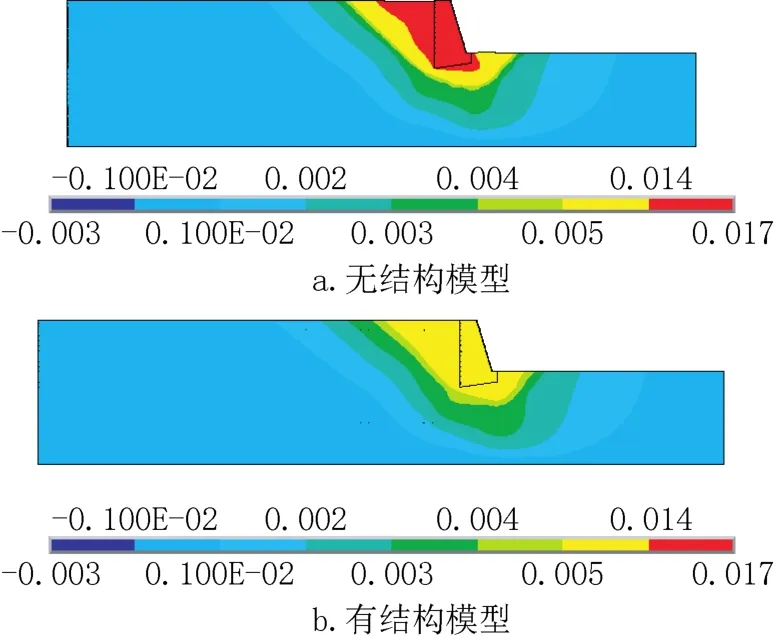
图5 土体和挡土墙Ux位移云图（单位：m）Fig.5 TheUxdisplacement contour image of soil and retaining wall（unit：m）

3.2 边坡对建筑桩基的影响

用ANSYS的路径功能在桩基的沿Z方向-0.4m～0.4m不同高度处取水平的路径，把X方向应力Sx映射在路径上，Sx对路径长度积分得到桩后推力和桩前抗力的总的分布力，如图6所示。

图6中的桩后推力和桩前抗力的分布力相减，得到用来设计桩基的设计推力，如图7所示。由图7可知设计推力在桩埋深接近5.5m位置为0，此处为桩基穿越边坡滑裂面的位置。在滑裂面以上，桩基承受土体向坡方向的推力，推力的分布呈抛物线的形状。在滑裂面以下，桩基承受土体背坡方向的抗力。

3.3 桩到坡顶距离的影响

图6 桩后推力和桩前抗力分布力Fig.6 The distributed force in front of pile and behind pile

桩到坡顶的距离以及桩与边坡潜在滑动面的相对位置对桩与边坡相互作用影响很大。模型编号及右桩到坡顶的距离如表2所示。

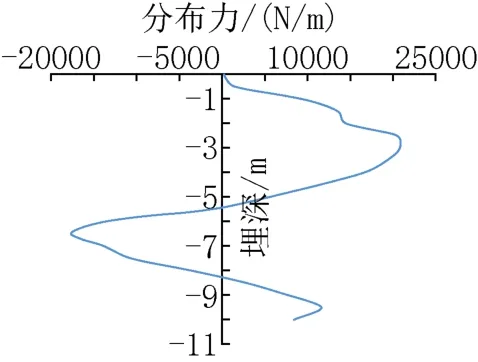
图7 设计推力（一）Fig.7 The design pushing forceⅠ

表2 右桩到边坡距离参数Tab.2 Pile slope distance parameter

由图8可知，在极限状态下，建筑桩基到坡顶的距离变化对挡土墙土压力的影响较小，d2模型的土压力变得更小，主要是因为桩基发挥了类似抗滑桩的作用。

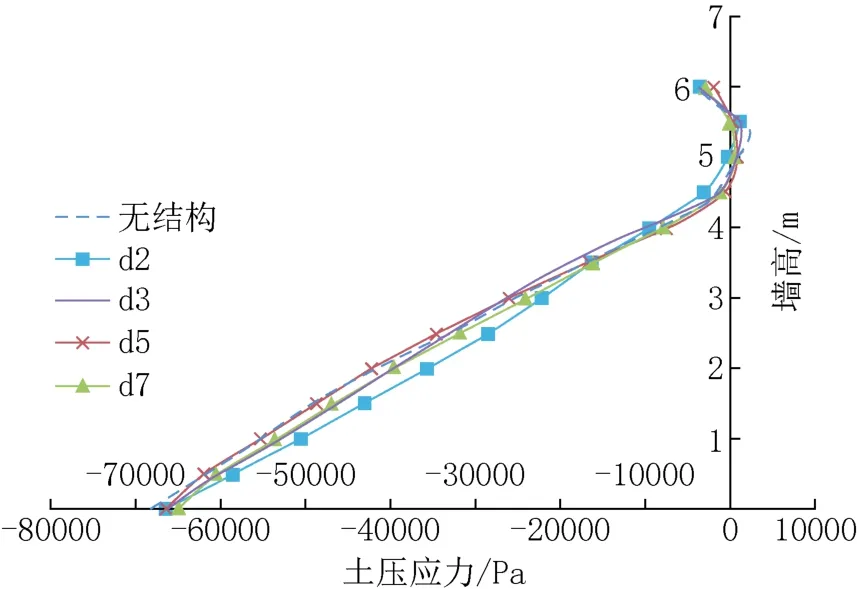
图8 平均土压应力Fig.8 The average earth pressure of retaining wall

由图9可知，随着建筑桩基到坡顶的距离变大，桩基的设计推力变小。d2、d3、d5、d7模型的最大推力分别为23.18kN/m、20.79kN/m、8.45kN/m、3.75kN/m，后三者分别为d2模型最大推力的89.69%、36.45%、16.18%。由设计推力零点位置可以看出桩基穿过滑裂面的位置，d2模型右桩穿过滑裂面的位置在埋深6m附近，d3模型右桩穿过滑裂面的位置在埋深5.5m附近，d5、d7模型右桩穿过滑裂面的位置分别在埋深4m、2m附近。

4 算例取值

《建筑边坡工程技术规范》［4］中7.2.3条规定，当基础外边缘到边坡距离a小于0.5H（边坡高度）时，侧向岩土压力取静止土压力；当0.5H≤a≤1.0H时，侧向岩土压力取静止土压力和主动土压力的平均值；当a＞1.0H时，侧向岩土压力取主动土压力，即不考虑建筑基础对挡土墙的影响。

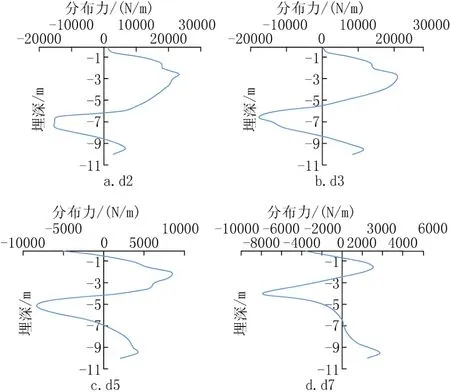
图9 设计推力（二）Fig.9 The design pushing forceⅡ

由于本文算例的边坡滑动面在45°左右，所以规范中规定当a＞1.0H时，建筑基础在边坡的滑裂面以外，侧向岩土压力取主动土压力，即不考虑建筑基础对挡土墙的影响是可取的。

5 结语

当边坡处于极限状态时，如果桩基的底部在滑动面以下，靠近挡土墙的桩基对挡土墙上的土压力基本没有影响，边坡内的桩基对边坡起到类似抗滑桩的有利作用。在设计坡体内桩基时，应根据边坡的实际情况计算边坡推力，计算配筋。