基于云模型QFD的产品服务系统工程特性重要度分析

耿秀丽,徐轶才

(上海理工大学 管理学院，上海　200093)

0　引言

产品服务系统(Product Service System, PSS)是产品设计与服务设计高度集成的系统，其目的是最大限度地满足顾客需求。方案设计是PSS设计的首要环节，对最终设计结果质量的影响最大。因此，PSS设计的核心问题是如何依据顾客需求进行方案设计。质量功能展开(Quality Function Deployment, QFD)作为一种顾客需求驱动的方案设计方法与工具，能够有效地帮助设计者解决PSS方案设计问题。

通常QFD包含方案规划、零部件配置、工艺规划和生产规划4个阶段。其中：方案规划阶段的主要目的是将顾客需求映射到具体的工程特性中，最终通过顾客需求重要度和顾客需求与工程特性之间的关联关系矩阵来确定工程特性重要度。方案规划阶段的核心就是确定工程特性的重要度，而顾客需求重要度的确定是其前提。在确定顾客需求重要度方面，文献[1]提出基于粗糙集的顾客需求重要度确定方法；文献[2]提出运用三角模糊数处理QFD评价信息的方法计算顾客需求重要度。运用粗糙集或模糊数可以解决QFD评价过程中存在的模糊性问题，但是不能解决QFD评价信息中的随机性问题。云模型是一种能实现定性概念与定量信息之间不确定性转换的模型，其数字特征熵En同时反映了定性概念的模糊性和随机性，并揭示了二者的关联性[3]。目前云模型已被广泛应用于信息处理、知识发现、人工智能和决策评价等方面。文献[4]将云模型应用到巷道的冒顶风险评价中；文献[5]提出了基于前景理论及云模型的多准则决策方法；文献[6]提出了基于云模型的信任评估方法。本文将云模型引入到QFD的重要度评价中，解决了QFD评价信息中的模糊性和随机性问题。

采用云模型处理QFD评价信息，将顾客/专家对顾客需求重要度的评价转化为云模型，通过云图可以同时反映评价信息的模糊性和随机性；然后通过顾客需求重要度与关联关系矩阵的乘积计算工程特性重要度。由于顾客需求重要度和关联关系矩阵都是以云模型表示的，无法直接相乘得到一个精确数值。因此，如何计算两组云模型之间的乘积是一个难点。文献[7]提出采用相对偏好关系分析计算两组三角模糊数的乘积，解决了三角模糊数不能直接相乘的问题。基于此，本文提出云相对偏好关系分析方法来计算两组云模型之间的乘积。采用云相对偏好关系分析计算各评价云模型与均值的相对偏好关系，将重要度或关联关系评价云模型转换成精确数值，进而计算工程特性的重要度。

为得到更准确的工程特性重要度，有必要对基于顾客需求重要度所确定的工程特性重要度进行修正。文献[8]和文献[9]在确定工程特性最终重要度时均考虑了对技术竞争性的分析，有效提高了重要度的准确性。故本文提出基于技术竞争性评估矩阵的工程特性重要度修正方法，先采用所提云相对偏好关系分析处理技术竞争性评估矩阵，再结合信息熵法确定各工程特性的重要度修正因子，进而确定最终的工程特性重要度。

本文采用云模型处理QFD评价信息，通过逆向云发生器生成评价信息的云模型，然后利用所提出的云相对偏好关系分析计算出工程特性初始重要度。在此基础上，通过分析技术竞争性评估矩阵对初始重要度进行修正，进而确定工程特性的最终重要度。最后，以某机械制造企业一款装载机的产品服务系统工程特性重要度分析为例，验证了所提方法的有效性。

1　云模型

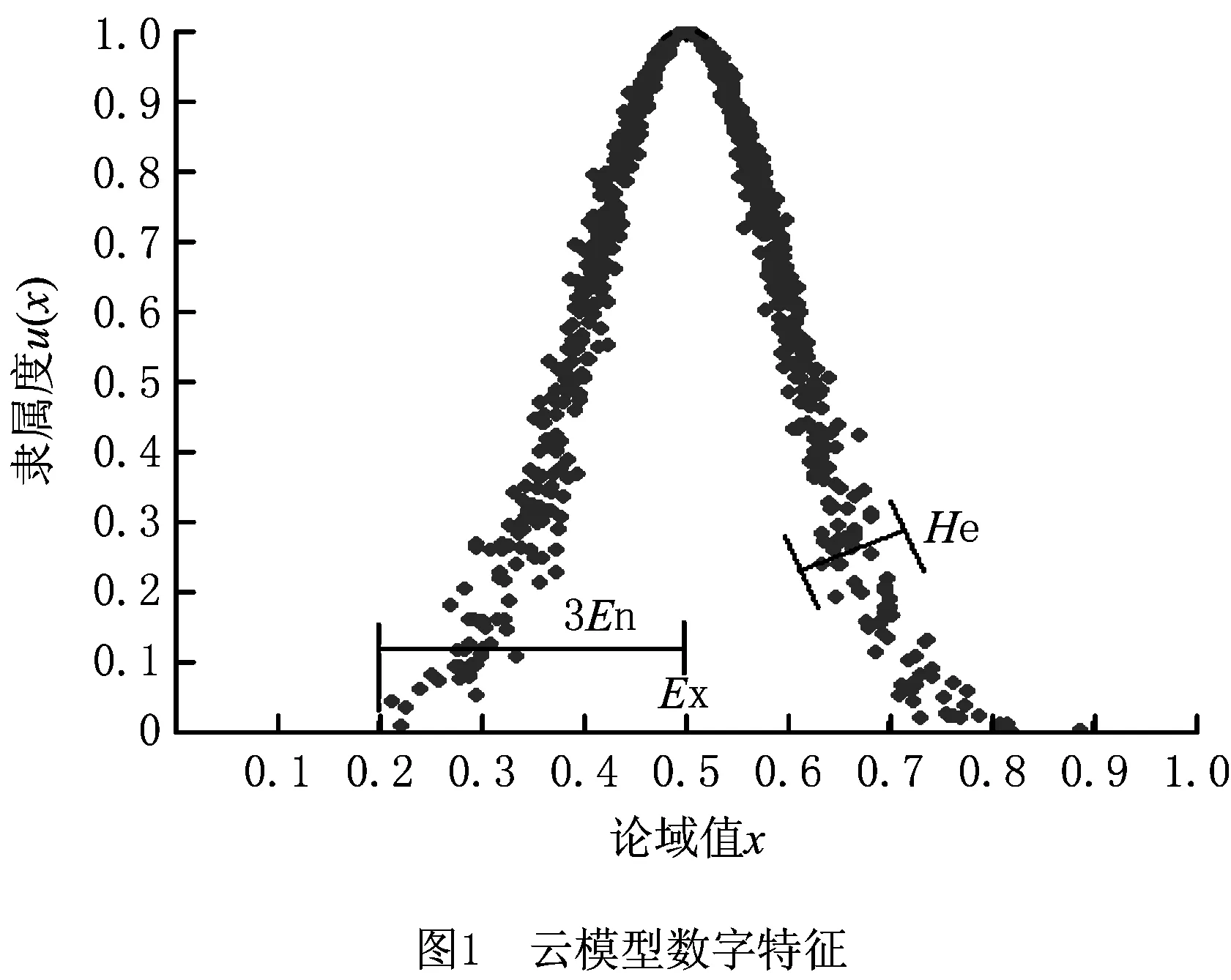
云模型是由李德毅院士于1995年首次提出，是一种能够实现定性概念和定量信息之间相互转换的模型。云模型通过数字特征反映定性概念，其表现形式为(Ex，En，He)，具体如图1所示。其中：Ex是最能够反映对应定性概念的数值。En一方面反映了定性概念被论域中的值所能接受的范围，即度量了模糊度；另一方面反映了论域中的值能代表这个定性概念的概率，即代表定性概念的云滴出现的随机性[3]。En同时反映了定性概念的模糊性和随机性，也揭示了它们之间的关联性[3]。通常，En越大，概念越宏观，模糊性和随机性也越大，确定性量化越难[3]。He是对En的不确定性的度量，它反映了En的离散程度，He值越大则云的厚度越大[3]。

1.1　云模型及其运算规则定义

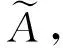
定义2[11]假设有两朵云，分别为A(Ex1,En1,He1)和B(Ex2,En2,He2)，其运算规则如下:

1.2　云发生器

1.2.1正向云发生器

正向云发生器是能实现定性概念转变为定量信息的数学模型，该模型对应实现算法的具体步骤如下：

(1)输入已知定性概念对应的云模型数字特征(Ex，En，He),云滴数y。

(2)生成一个满足正态分布N(En，He2)的正态随机数，记为En′。

(3)生成一个满足正态分布N(Ex，En′2)的正态随机数，记为x。

(5)生成一个云滴(x，μ)。

(6)重复步骤(2)～步骤(5)，直到生成y个云滴。

1.2.2逆向云发生器

逆向云发生器与正向云发生器功能相反，它是实现定量信息转换为定性概念的模型。逆向云发生器的算法按照是否利用确定度信息可分为需要和不需要两种。本文选取后者，采用文献[12]提出的逆向云算法，仅利用样本云滴的定量值来计算定性概念的云模型数字特征，其具体步骤如下：

(1)输入z个评价指标定量值xi(i=1,,z)。

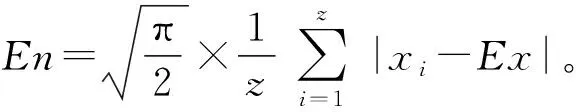
巴赫金认为：“文类在历史演变之中可能出现一种创造性记忆，文类不仅能持续保持自己的统一框架和连续性，它还能不断地在更高的水平上复活自己；一种文类愈加完善，它同时将愈加充分地回忆起自己的过去。”(巴赫金,1988:165)因此，模仿发展成熟的文体而又对其突破，唤起读者文学记忆的同时，又达到了推陈出新的目的。这种被模仿的文类主要包括武侠小说、侦探小说、科幻小说、神话等，这些文类都有自己非常突出的形式特征，所以容易被模仿。《爵士乐》采用了典型的侦探小说模式。

2　考虑云相对偏好关系分析的云模型QFD计算

2.1　采用云模型处理QFD中的评价信息

将QFD各部分评价的专家打分作为输入，采用逆向云发生器生成各评价云模型。通过云图的绘制以及云模型中熵的大小反映评价信息的模糊性和随机性。超熵也能反映评价信息的随机性，若云模型的超熵值较大，即云图厚度大，则说明专家所给评价值的隶属度随机性大。现实应用中可参考超熵进行评价信息的反馈整理。由于反馈整理过程繁琐，本文不考虑信息反馈。

假设通过市场调研获得了QFD方案规划中的顾客需求，记为Ci(1≤i≤m)，再将顾客需求映射到具体的工程特性，记为Ej(1≤j≤n)。采用给定的评分集，请专家对各项顾客需求的重要度、顾客需求与工程特性之间的关联关系和工程特性的竞争性进行评价。例如：专家采用1～10进行评价，位于不同区间的评价值具有不同的等级含义，各评价等级对应的分值区间如表1所示。

表1　各评价等级对应的分值区间表

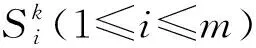
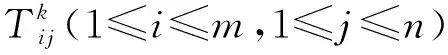
根据QFD的重要度计算方法可以得到工程特性Ej的重要度wj计算公式如下：

(1)

2.2　考虑相对偏好关系分析计算工程特性重要度

式(1)中的Ai和Bij均以云模型的3个数字特征形式表示，都不是精确数值，无法直接相乘计算工程特性重要度。模糊相对偏好关系分析可以解决两组模糊数不能直接相乘的问题，其原理是通过计算各三角模糊数与该组模糊数均值的相对偏好关系，间接将其转换成精确数值。本文提出云相对偏好关系分析方法，用以计算两组云模型的乘积。所提云相对偏好关系是以一组云模型的均值为基准，计算各云模型与均值的相对偏好关系，进而将其转换成精确数值。

(2)

式中：

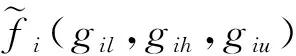
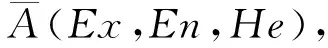
(3)

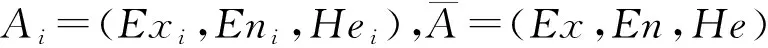
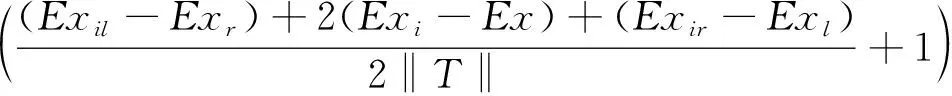
(4)

式中：Exil=Exi-3Eni，Exir=Exi+3Eni，Exl=Ex-3En，Exr=Ex+3En；

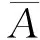
(5)

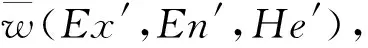
3　产品服务系统工程特性重要度修正分析

基于顾客需求重要度计算得出的工程特性初始重要度，由于没有考虑到技术竞争性评估，还不够准确，需要进行修正。修正方法的基本思路是先采用所提云相对偏好关系分析处理竞争性评估矩阵，将竞争性评价云模型转换成精确数值，再采用信息熵法计算工程特性重要度的修正因子，确定工程特性最终重要度，具体修正方法如下。

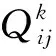
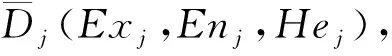
(6)

M1=

对企业而言，若其产品的某项工程特性Ej在行业中处于领先水平，则企业应该继续保持或者扩大竞争优势，适当提高Ej的重要度；若Ej在行业中各企业的水平接近，则说明该项工程特性不是很重要或者已达到技术瓶颈，因此应该适当降低Ej的重要度；若Ej在行业中处于很差的水平，则需要对其进行改进以缩小差距，因此应适当提高Ej的重要度。信息熵能很好地反映信息的离散性，信息越趋于一致，熵值越大，信息越离散，熵值越小[13]。因此，本文将所提出的云相对偏好关系分析法与信息熵法相结合，进而确定各工程特性重要度的修正因子。

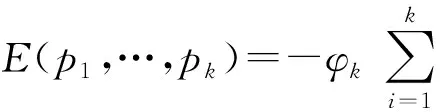
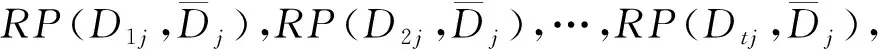
(7)

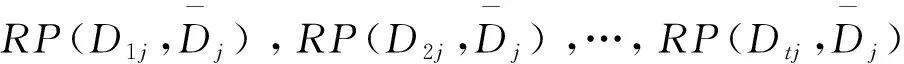
(8)

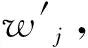
(9)

(10)

4　案例分析

某企业是一家知名的机械制造企业，主要制造装载机，其装载机有4大类型：小型装载机、石材叉装机、燃气型装载机和大中型装载机。针对市场中的一类客户群，为提升顾客满意度，该企业欲对其产品进行改进。但因资源有限，企业必须确定产品各工程特性的改进优先级，以合理分配资源，从而最大限度地满足顾客需求。本文以该企业的一款额定载荷为3 t的装载机为例，采用所提方法确定其工程特性的重要度，为企业改进该产品提供依据。

该企业通过市场调研获取了6项顾客需求：动力强劲(C1)、灵活高效(C2)、易操控(C3)、稳定可靠(C4)、服务及时(C5)和低能耗(C6)。由专业人员给出该装载机的工程特性，分别为：发动机额定功率(E1)、最大掘起力(E2)、斗容量(E3)、最大卸载高度(E4)、三项和时间(E5)、最小转弯半径(E6)、变速操纵方式(E7)、预防性维修策略(E8)、服务响应效率(E9)、服务完成效率(E10)、节能方案(E11)和尾气排放标准(E12)。

由于产品经理和售后服务工程师对顾客需求及其与工程特性间的关联关系和工程特性的竞争性都有较深的认识，故选取10位产品经理和10位售后服务工程师组成专家组。给定评分集，如表1所示。专家采用1～10之间的精确数对各项顾客需求重要度进行打分。然后以专家的打分为输入，利用逆向云发生器生成各项顾客需求重要度的评价云模型。最后利用式(3)～式(4)计算出各项顾客需求的相对重要度，计算结果如表2所示。

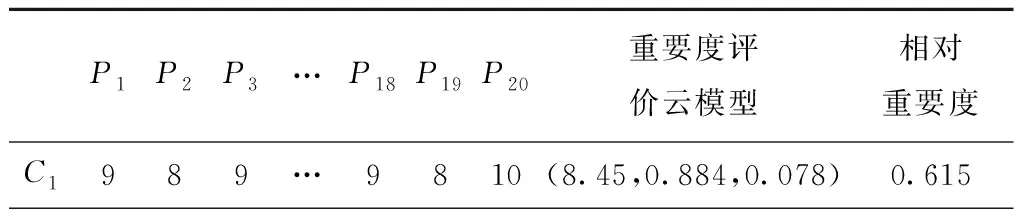
表2　顾客需求重要度评分及其相对重要度

续表2

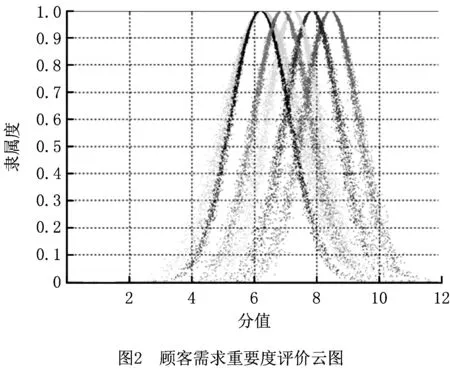
为直观反映表2中各项顾客需求的重要度评价云模型，利用正向云发生器生成相应的云图，具体如图2所示。从左到右依次为顾客需求C4，C5，C6，C3，C2，C1的重要度评价云图。云图可以很好地反映出各项需求重要度所属的等级，以及评价信息模糊性和随机性的大小。例如：图2中从左数第一、二个云图分别是顾客需求C4和C5的重要度评价云图，从图中可以看到C4和C5的重要度评价分值均处于[5,7)之间，属于“一般”等级。C4和C5的重要度很接近，一般方法难以再继续深入加以分析。但是从图2中可以看出，C4的云图跨度及云厚度均大于C5，跨度越大说明模糊性越大，厚度越大说明随机性越大，因此得出C4重要度评价信息的模糊性和随机性都比C5要大，即C4重要度评价的可靠性比C5差。与本文所提方法相比，传统QFD计算中采用的精确数值法则仅仅只能得到各项顾客需求的重要度大小，无法反映其他信息。

同理，再由20位专家对顾客需求与工程特性的关联关系进行打分。以专家打分为输入，利用逆向云发生器生成关联关系评价云模型，具体结果如表3所示。

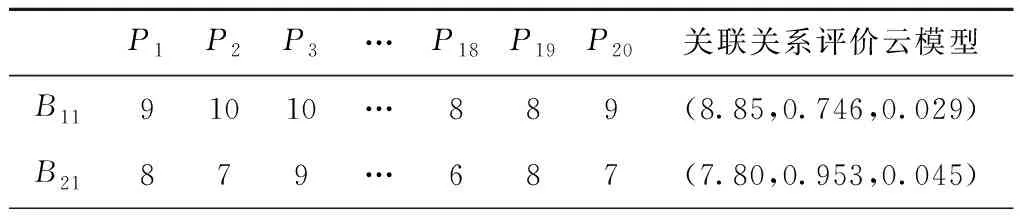
表3　顾客需求与工程特性关联关系评价结果

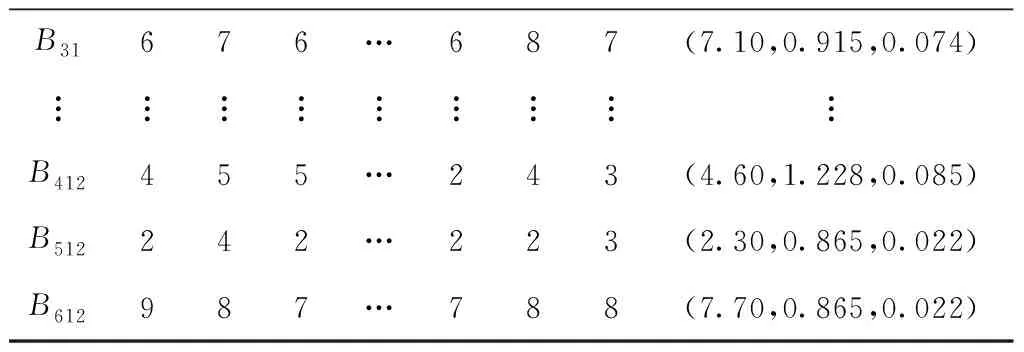
续表3

再将表3中数据进行整理，即可得到云模型关联关系矩阵，具体如表4所示。根据顾客需求相对重要度和关联关系矩阵，利用式(5)计算各工程特性的重要度评价云模型。最后，利用式(3)～式(4)计算出工程特性的初始重要度，其结果依次为0.627，0.618，0.551，0.386，0.544，0.397，0.525，0.366，0.521，0.538，0.468，0.458。

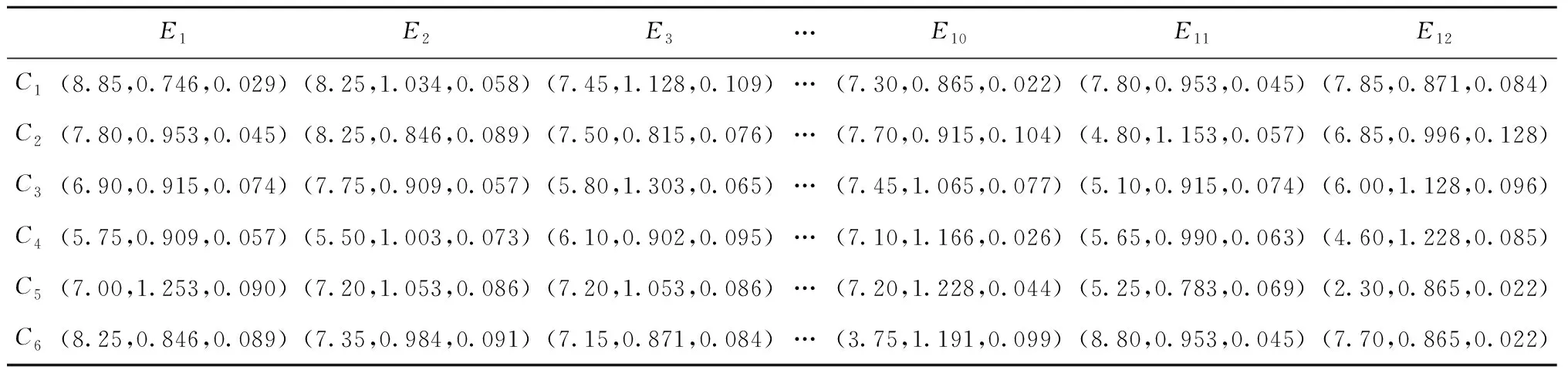
表4　顾客需求与工程特性云模型关联关系矩阵

考虑技术竞争性评估矩阵来修正工程特性的初始重要度。首先，由20位专家对包括本企业在内的6个企业各项工程特性进行竞争性评估打分；再以专家打分为输入，利用逆向云发生器生成各企业的工程特性竞争性评价云模型，即得到技术竞争性评估矩阵，具体如表5所示。

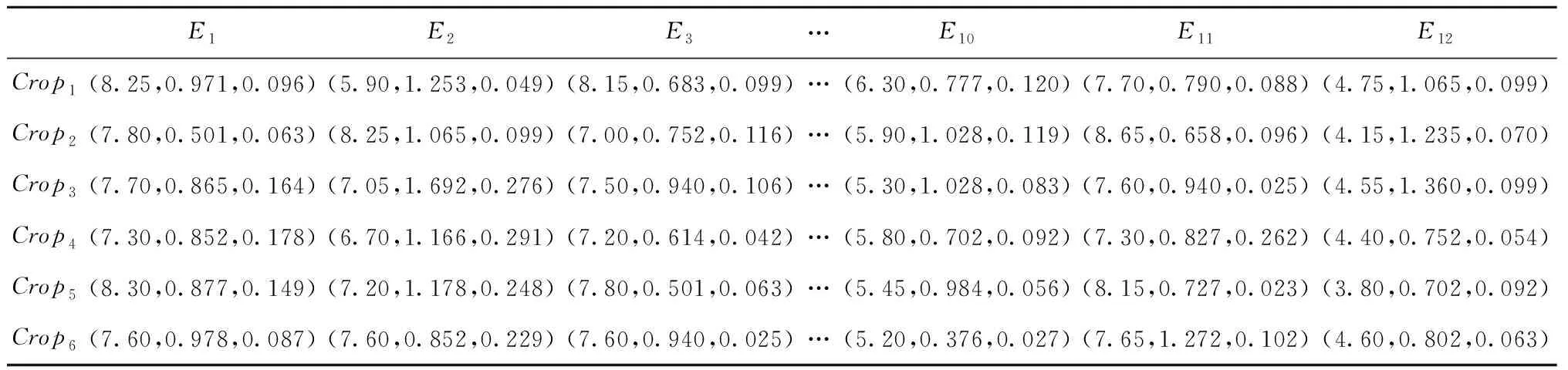
表5　技术竞争性评估矩阵

利用云相对偏好关系分析对表5所示的技术竞争性评估矩阵进行处理，利用式(2)～式(3)将各竞争性评价云模型转换成精确数值，结果如表6所示。

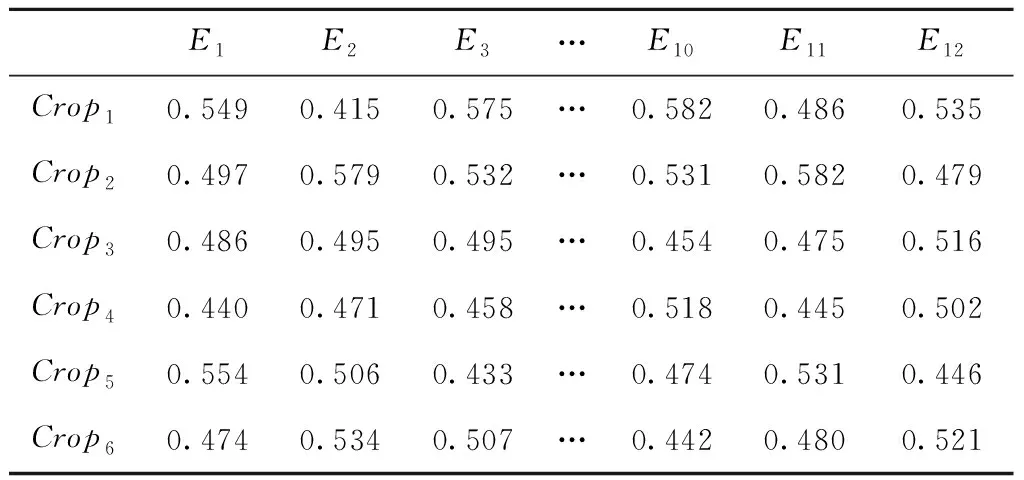
表6　基于云相对偏好关系分析的技术竞争性评估矩阵

根据表6中的数据，采用信息熵法来计算各工程特性重要度的修正因子。以工程特性E1的重要度修正因子计算为例。则有：

RP1=0.549+0.497+0.486+0.440+

0.554+0.474=3;

p11=0.549/3=0.183，p21=0.497/3=0.166，

p31=0.486/3=0.162；

p41=0.440/3=0.147，p51=0.554/3=0.185，

p61=0.474/3=0.158。

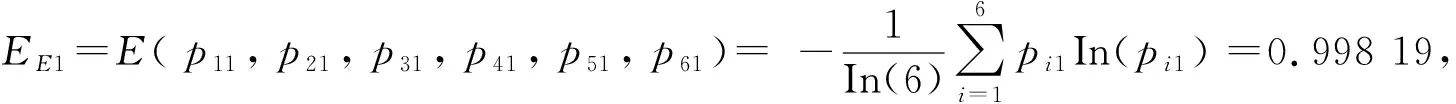
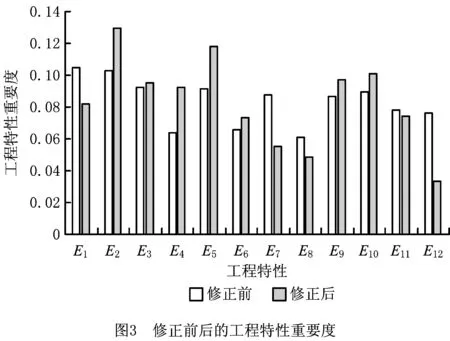
为直观地反映修正前后工程特性重要度的变化，将修正前后的重要度绘制成直方图来进行比较，具体如图3所示。显然，修正前后各重要度均发生了明显变化。例如：修正前E1的重要度最大，修正后E2的重要度最大。其原因是专家对工程特性的竞争性评价表明，各企业的工程特性E1都处于较好的水平，差距不大，故由式(7)和式(8)可知，其由熵值确定的重要度修正因子e1较小，而专家评价表明工程特性E2在行业中各企业之间水平相差较大，且本企业E2目前处于最差水平，故其由熵值确定的重要度修正因子e2较大。e1和e2的大小分别为：0.065 6和0.105 1，因此，修正后E1的重要度相对降低，而E2的重要度相对提高。总体而言，修正前按重要度从大到小对工程特性的排序为：E1，E2，E3，E5，E10，E7，E9，E11，E12，E6，E4，E8；修正后的排序为：E2，E5，E10，E9，E3，E4，E1，E11，E6，E7，E8，E12。因此，企业应该将资源重点用在改进工程特性E2，E5和E10上。

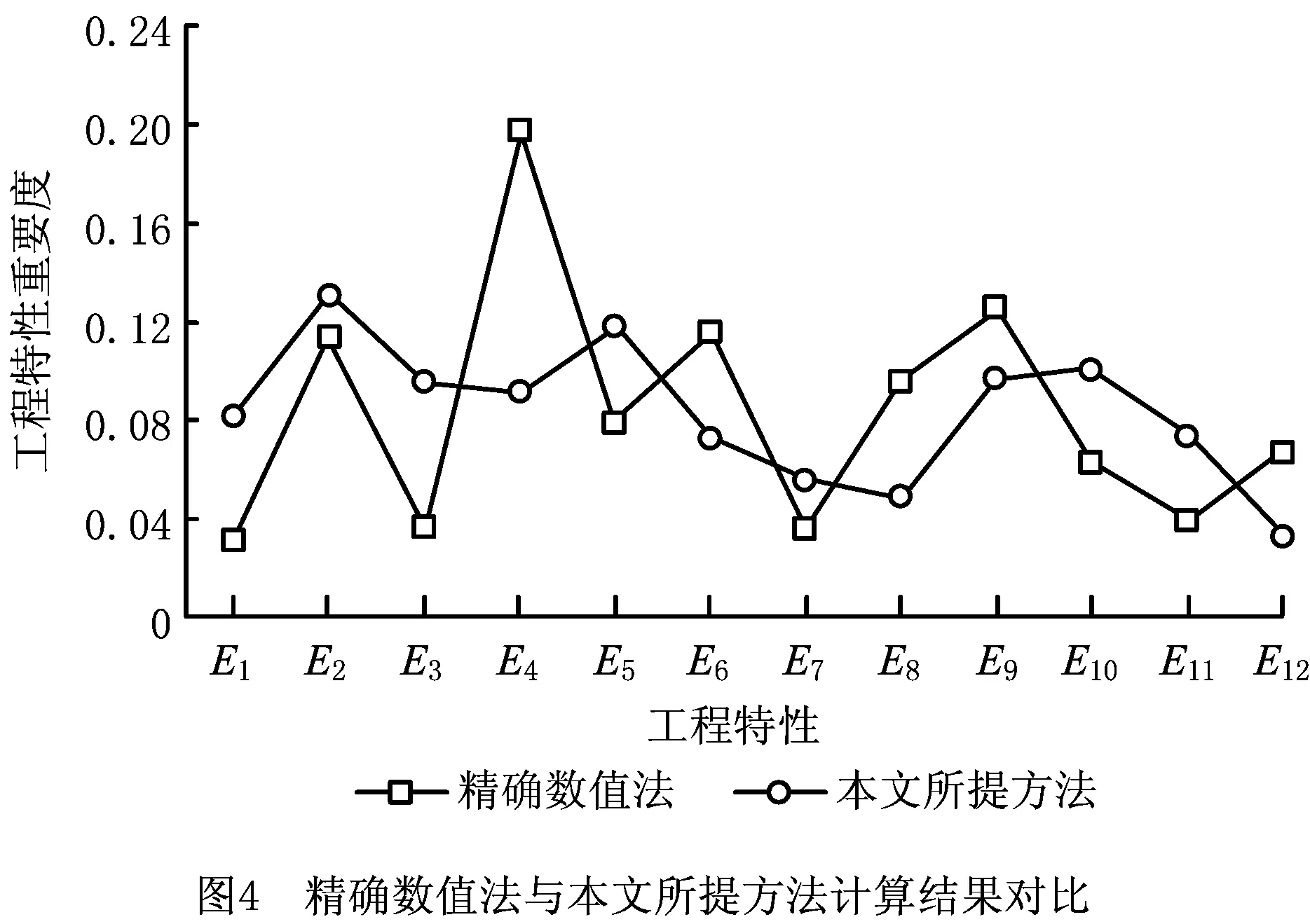
另外，为反映本文所提方法的有效性和可行性，将传统QFD计算所采用的精确数值法与本文所提方法进行比较。以表2、表3中的数据为例，传统QFD计算中所采用的精确数值法一般是直接将表2中各项顾客需求的重要度打分取算数平均值，再通过将各项均值除以均值之和来确定顾客需求重要度。然后对表3中的分值数据进行处理，求出各项关联关系打分的均值，再将确定的顾客需求重要度和关联关系均值代入式(1)，最后作归一化处理即得各工程特性基本重要度。利用精确数值法计算出工程特性E1～E12的基本重要度并进行修正，得最终重要度分别为：0.032，0.114，0.036，0.198，0.080，0.115，0.036，0.095，0.125，0.063，0.040，0.067。

图4为精确数值法与本文所提方法的结果对比图。通过图4可以看出，两种方法所计算出的工程特性重要度大小存在明显差距。按工程特性的重要度从大到小对工程特性进行排序，得到精确数值法对应的排序为：E4，E9，E6，E2，E8，E5，E12，E10，E11，E3，E7，E1，而本文所提方法确定的排序则为：E2，E5，E10，E9，E3，E4，E1，E11，E6，E7，E8，E12。产生这些差异的主要原因是精确数值法未能考虑到专家评价信息的模糊性和随机性，而本文采用云模型来处理专家的评价信息，通过将能同时反映评价信息模糊性和随机性的熵值En纳入工程特性重要度计算中，较好地解决了评价信息的模糊性和随机性问题，从而提高了工程特性重要度的准确性。

上述对比分析表明，采用本文所提方法能够更准确地确定工程特性重要度，从而有效指导企业进行产品改进。

5　结束语

PSS工程特性重要度的确定是PSS方案设计的关键，而QFD作为一种很好的方案设计工具，能有效地计算PSS工程特性重要度。针对传统QFD中计算工程特性重要度时未能解决评价信息的随机性问题，本文提出一种基于云模型QFD的产品服务系统工程特性重要度分析方法。所提方法的特点有：

(1)采用云模型处理QFD评价信息，同时解决了评价信息中的模糊性和随机性问题，并提出云相对偏好关系分析计算出基于顾客需求重要度的工程特性初始重要度。

(2)考虑技术竞争性评估矩阵，采用所提云相对偏好关系分析法和信息熵法确定工程特性重要度修正因子，进而确定最终的工程特性重要度。

通过对某企业的装载机产品服务系统工程特性重要度分析，验证了所提方法的有效性和可行性。不少论文都采用Yager值对信息的反模糊化进行了评判比较，下一步研究将深入考虑和分析Yager值与相对偏好关系分析的优劣，提出改进的云模型量化方法。此外，还将研究本文所提方法的原型系统开发。