基于维护效率的设备多目标预防维护优化建模

方玲珍，史凯龙，陆　彪，周晓军

(上海交通大学 工业工程与管理系，上海　200240)

0　引言

设备的预防性维护一直是维护领域的研究热点，通过合理的预防维护保障设备性能是制造企业降低运行成本、提高生产效率和市场竞争力的重要途径。随着我国经济的快速发展，资源环境约束日益突出，企业愈发追求用更少的资源消耗获得更大的经济效益，如何提高维护活动的投入产出效率已成为当务之急。

传统的维护决策多将维护视作一项投入型活动，并试图从降本着手为企业优化维护计划。Doostparast[1]以设备可靠性为中心建立了基于维护总成本的预防维护优化模型；王华[2]引入了备件成本，并通过最小化租赁维护总成本获取维护计划；Lu[3]考虑了设备衰退对产品质量的影响，构建了包含质量损失的维护总成本目标函数；张博文[4]将成组维护策略集成到生产计划决策中，建立了生产与维护的联合决策模型，在保障生产前提下尽量减少生产与维护的总成本。而随着生产效率的不断提升，企业对设备高可靠性的依赖程度逐步增大，维护已成为企业的利润来源。为此，也有学者从产出效益的角度来建模并量化维护价值。Alsyouf[5]提出维护决策时需考虑维护改善设备可靠性带来的价值；Jiang[6]以开动率为目标进行维护建模，最小化设备的平均停机时间；Marais[7]用不同状态下的系统产出来描述维护价值，进而建立了一种基于马尔科夫决策过程的动态预防维护策略；Liu[8]围绕系统中零部件的维护价值定义可靠度函数，并以维护价值最大化为目标建立了多部件系统的预防维护模型。综合来看，以上投入型和产出型模型在提高设备生产效率、降低设备维护成本方面都发挥了重要作用。然而，上述模型均没有考虑维护投入与维护产出的相关关系，无法实现维护效益的最大化。事实上，已有不少学者通过多目标建模的方式来解决维护投入与产出的平衡问题。夏唐斌[9]整合维护成本率和设备开动率，建立了动态预防性维护的多目标决策模型；陆志强[10]运用模糊加权平均优化算法，综合考虑单位时间成本和制造系统设备开动率，建立了多目标维护决策模型；崔维伟[11]以工件流程时间最短和维护成本最小为联合优化目标构建了生产与维护的决策模型，并设计了改进的遗传算法进行求解。可以看出，以上模型综合考虑了维护和生产相关的多个目标，是对现有维护理论的有益拓展。不过，这些模型对权重因子的取值多基于经验或定性分析方法(如层次分析法)，没有客观的定量分析依据。此外，以上研究也未考虑维护资源的利用效率，尚缺乏从效率角度实现维护决策的建模思路。

本文聚焦于设备的维护效率，将其定义为维护投入产出比，以维护直接成本为投入，以涵盖设备开动率和产品合格率的多目标维护效果为产出，进而以各指标单位变动所影响的产品数量为基准分配指标权重，建立了多目标维护效率函数与设备预防维护模型，从而获得设备的最优维护计划。

1　问题描述

考虑一机加工设备，在维护规划期内稳定地生产某一种产品。随着设备使用时间增加，其磨损、疲劳等老化过程加剧，导致设备可靠性逐渐恶化。在设备失效前，其可正常运转但以一定的概率产出次品。随着设备状态恶化，次品率逐步上升。基于这一事实，设备性能的变化拟通过设备可靠性和产品质量的状态来衡量。设备的可靠性指标采用维护周期内设备的开动率来表征，而输出产品的质量状态则用维护周期内产品的合格率来表示。在此基础上，整合设备开动率和产品合格率构建多目标维护效果以衡量维护活动的产出，其中，各指标权重由其单位变动所影响的产品数量决定。

对于机加工设备，影响产品质量的因素众多，本文将设备中对产品质量有显著影响的部件称为质量相关部件。质量相关部件是设备的重要组成部分，其性能的衰退不仅会导致产品质量的衰退，还会影响设备的故障率。为表征以上影响机理，拟通过集成设备历史故障信息和质量相关部件的状态信息对设备进行故障率建模，进而得到设备开动率指标；通过响应模型量化质量相关部件衰退与产品质量衰退的关系，进而得到产品合格率指标。

设备发生故障时，实施小修修复，小修不改变设备的损害情况，只恢复设备的正常运行。每经过固定的时间周期T即对设备实施预防维护，预防维护可使设备回到全新状态。假设每次预防维护和小修的时间及成本不变。

2　维护决策优化模型

质量相关部件衰退不仅影响设备开动率，还会导致其输出产品的质量特征发生偏移，影响产品合格率，故需先对质量相关部件的退化过程进行建模。为此，机加工设备的维护决策建模可分为质量相关部件退化建模、设备开动率建模、产品合格率建模和维护策略优化建模4个步骤。

2.1　质量相关部件退化过程建模

由于维护可改善质量相关部件，将表征质量相关部件衰退的特征参数称为可控过程变量，如刀具或夹具的磨损等，假设这些变量均为以时间为参数的函数且相互独立，记为X(t)=[X1(t),X2(t),,Xn(t)]T。其他不能由维护改变的随机因素称为噪声变量，如人为和环境因素等，记为Z=[Z1,Z2,,Zl]T。

在设备使用过程中，质量相关部件的负载情况、内部状态和外部环境的改变使得退化过程具有随机和动态的特征，而Wiener过程可有效描述此类随机过程，已被广泛应用于退化建模[12-14]，因此本文采用该过程来模拟质量相关部件的衰退过程，可表示为

Xi(t)=Xi(0)+μit+σiωi(t),i=1,2,,n。

(1)

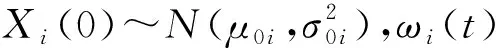
(2)

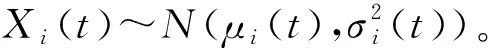
(3)

2.2　设备开动率建模

维护领域内设备开动率一般可定义为设备实际运行时间与总时间的比值[15]，因此，本文根据单个维护周期内设备的工作时间和维修时间构建设备开动率指标，定义为

(4)

式中：Tp为单次平均预防维护时间，Tc为单次平均小修时间，H(T)为预防性维护周期T内设备的累积故障次数。Tp和Tc可以通过统计历史维修数据得到均值，因此，要得到开动率，关键在于设备的故障率建模以计算累积故障次数。

作为关键部件，质量相关部件状态差异对设备故障率有着显著影响。本文基于比例故障率模型(Proportional Hazard Model, PHM)对设备故障率进行建模，以实现对设备老化信息和质量相关部件信息的综合考虑[16]，设备故障率函数表示为

κ(t)=λ(t)e[βX(t)]=λ(t)e[β1X1(t)+β2X2(t)++βnXn(t)]。

(5)

式中：t为设备有效运行时间,λ(t)是基本故障率函数，表示设备的老化过程，e[βX(t)]是连接函数，表示X(t)对设备故障率的影响，β∈Rn,βi为回归参数,表示Xi(t)对设备故障率的影响。Xi(t)退化服从Wiener过程，t时刻Xi(t)具有不确定性，因此t时刻设备的故障率h(t)为κ(t)的期望值，可表示为

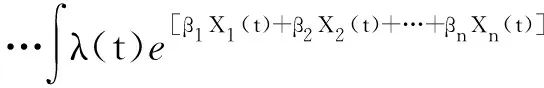
f[X1(t),X2(t),,Xn(t)]

dX1(t)dX2(t)dXn(t)。

(6)

由于Xi(t)相互独立，则有

(7)

将Xi(t)的概率密度函数式(3)代入式(7)，可得

(8)

将式(2)代入式(8)，可得

(9)

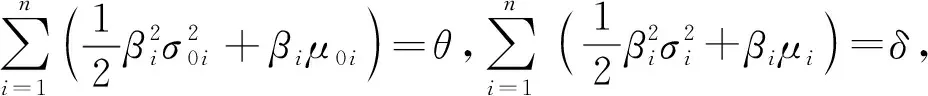
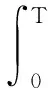
(10)

将式(10)代入式(4)，可得

(11)

2.3　产品合格率建模

随着质量相关部件的衰退，设备所加工产品的质量特征逐渐发生偏移，而响应模型能有效描述输出产品质量特征与过程变量的关系[3,17]。因此，本文针对机加工设备，通过响应模型得到维护周期内产品合格率的变化情况。通常，设备加工的产品具有多个质量特征，将其随时间的衰退量记为Y1(t),Y2(t),,Ym(t)，基于响应模型，该衰退量可表示为

j=1,2,,m。

(12)

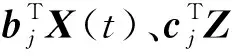
(13)

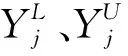
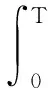
(14)

故平均合格品率Q(T)可表示为

(15)

2.4　周期性维护策略优化建模

以最大化维护效率即维护投入产出比为目标构建预防维护决策模型，为了衡量单位维护成本得到的产出，将维护效率η定义为

(16)

式中：TDC为设备维护直接成本，V为包含设备开动率和产品合格率的多目标维护效果。通常，维护成本包括预防维护成本、小修成本、生产损失成本和质量损失成本等。其中,预防维护成本和小修成本可视为维护直接成本，其决定了设备的性能状态，而生产损失和质量损失可视为维护直接成本投入所导致的间接成本，其由设备的性能状态所决定，反映维护活动的效果。基于这一考虑，本文将维护直接成本作为维护投入。假设Cp为单次平均预防维护成本，Cm为单次平均小修成本，则

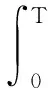
(17)

在此基础上，以设备开动率衡量设备可靠性，以产品合格率衡量输出产品的质量状态，综合考虑维护对两者的提高，引入权重因子wA和wQ(wA+wQ=1)，定义多目标维护效果V为

V=wAA(T)+wQQ(T)。

(18)

对于多目标维护决策问题，各目标权重的分配多基于专家经验或定性分析方法，如层次分析法[18]等，而以上方法很难获得全面准确的信息且带有主观性[19]。本文寻求指标自身的客观性标准，以各指标单位变动所影响的产品数量为基准定义分配权重wA和wQ，以避免传统方法带来的人为因素的影响。具体来说，可通过统计设备在较长一段生产时间T′内的生产数据来完成权重分配，包括：设备在时间T′内的开动率A(T′)、维修时间a、产品合格率Q(T′)、生产的不合格品数d、生产速率r。由于维修期间设备不能生产，维修时间视为损失的生产时间，则损失产量为LA=r×d。在此基础上，提高单位开动率带来的产品增量SA可表示为

(19)

提高单位合格品率带来的合格品增量SQ可表示为

(20)

增量SA和SQ均为产品数，故可通过增量SA和SQ分配设备开动率和产品合格率的权重，表示为

(21)

将式(17)和式(18)代入式(16)，可得维护效率表达式为

(22)

在此基础上，通过最大化维护效率η，确定最优的预防维护周期T*。

3　算例分析

3.1　算例介绍及优化结果

考虑一用于加工传动轴的卧式车床，传动轴零件图如图1所示。该零件直径50 mm，回转面的加工分为粗车、半精车、精车3个阶段。随着车床使用时间增加，刀具逐渐磨损，导致轴的直径慢慢偏离标准值，为此，将刀具视为质量相关部件。刀具的磨损为可控过程变量，记为X(t)，该传动轴直径偏移即为输出产品质量衰退，记为Y(t)，人为因素导致的误差为噪声变量，记为Z。机床处于全新状态时刀具磨损量为0，即X(0)≡0，Z～N(0,0.01)。传动轴直径的设计标准为φ50 mm，上下公差限分别为-0.025和0，故t时刻合格品率Q(t)=P{-0.025≤Y(t)≤0}，通过响应曲面法得到响应模型[20]

Y(t)=-0.009-0.79X(t)+0.008Z-

0.013X(t)Z。

(23)

而合格品率降至80%被认为不可接受，设经过时间U后设备生产的产品合格率降至80%，因此最优的预防维护周期T*∈(0,U)，通过式(23)求得U=29。

威布尔分布适用于描述机电类产品故障的分布形式[21-22]，选取基于威布尔分布的PHM模型来描述卧式车床的故障率分布函数，表示形式如下

(24)

式中α、γ分别为威布尔分布的形状参数和尺寸参数。根据以往文献中对威布尔比例故障率模型[23]和Wiener过程[24]的参数估计方法，结合车床的历史数据设定模型中参数取值如表1所示，表中小修和预防维护的平均成本和时间可通过统计车床日常生产数据得到。此外，由实际生产数据得平均每年维修时间100.69天，平均每天生产89件，平均每年次品数为2 678件。通过式(19)～式(21)可求得wA=0.58，wQ=0.42。

表1　模型参数表

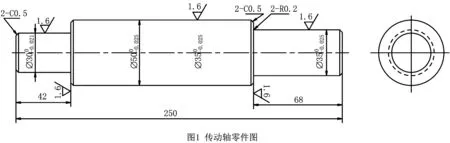
图2给出了在(0,U)内搜索步长为1的优化结果。图2显示，设备的最优维护周期T*=12，维护效率ηmax=432.446。随着设备维护周期的增长，维护效率呈现先升后降的变化趋势。这主要是因为维护周期过短易导致维护时间占用过多，进而使得设备开动率降低；而维护周期过长易导致设备故障频发，进而增加小修成本并影响产品合格率。可见，有效平衡维护的投入与产出才能实现维护效率的最大化。

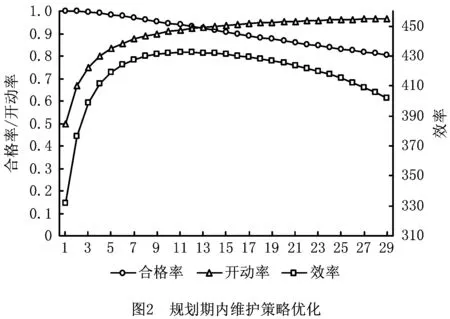
图3给出了其他因素不变的条件下，小修成本与预防维护成本单独变化对最优维护周期和维护效率的影响。图3显示，随着小修成本的增加，维护周期逐步缩短，应通过减少故障次数防止小修成本的过度增长；而随着预防维护成本的增加，维护周期相应变长，表明预防性维护代价较高时，应通过适当延长维护周期来提高维护效率。

3.2　对比分析

为了体现本文以效率为导向的维护决策模型的优越性，将其与传统的以成本率为目标的维护决策模型进行比较。预防维护可使设备修复如新，因此设备在每个维护周期的维护成本率均相等。根据文献[3]中的计算方法得到维护成本为

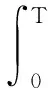
(25)

式中P(t)=E[qY(t)2]。由生产数据得到损失系数q=50.1 $/mm2。单个维护周期内的维护成本率可表示为

(26)

通过最小化目标函数可得到传统以成本率为目标的决策方法下的最优维护周期T*=63，维护成本率cmin=4.255，此时，维护效率η=43.373，产品合格率已经降至64.18%。而前文效率导向优化得到的最优维护效率ηmax=432.446，维护成本率c=16.475，产品合格率Q(T)=93.04%，虽然维护成本率是原来的3.87倍，但维护效率却达到了成本模型的9.97倍。可见，维护效率导向模型在保证维护效率和质量提升上都有更好的表现。这也验证了以维护效率为优化目标的有效性，维护效率能有效评估设备可靠性和产品质量多项指标，并较好地平衡维护的投入和产出，可满足企业的实际维护需求。

4　结束语

本文提出了维护效率的概念，从投入产出的角度出发，考虑质量相关部件衰退对设备故障率和产品质量衰退的影响，以单位维护成本的产出最大化为优化目标，构建了一种维护效率导向的设备预防维护模型。算例分析表明，传统的采用单纯追求成本最小化的维护建模方式，并不能完整地反映设备的维护需求，无法反映投入资源的利用效率。而效率导向的维护建模方式综合考虑了维护的投入产出比，可获得更高的维护效率，为设备的维护决策提供一种新的建模思路。未来针对多设备串并联制造系统，从效率角度出发建立多目标预防维护模型。