关于高考数学运算考查要求的几点建议——以2017年全国高考江苏卷为例

崔志荣

(江苏省东台市安丰中学　224221)

2017年高考已落下帷幕，江苏考生普遍感到数学试卷有一定难度，为此，笔者对江苏数学卷的一些“把关”题作了一点探讨，认为试卷的运算考查要求偏高.数学运算能力，当然是高考数学考查的一个重要指标，但要把握好度，尤其是计算机高速发展的今天，我们不需要培养人脑计算机，要培养学生的运算理念，强化运算程序的分析，那些繁杂的机械运算，可由计算机代劳.基于以上思考，本文将结合江苏数学卷的部分试题，以笔者个人对数学运算的理解，对高考命题提出几点建议，不足之处，敬请谅解！

1　把准运算定位

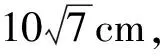
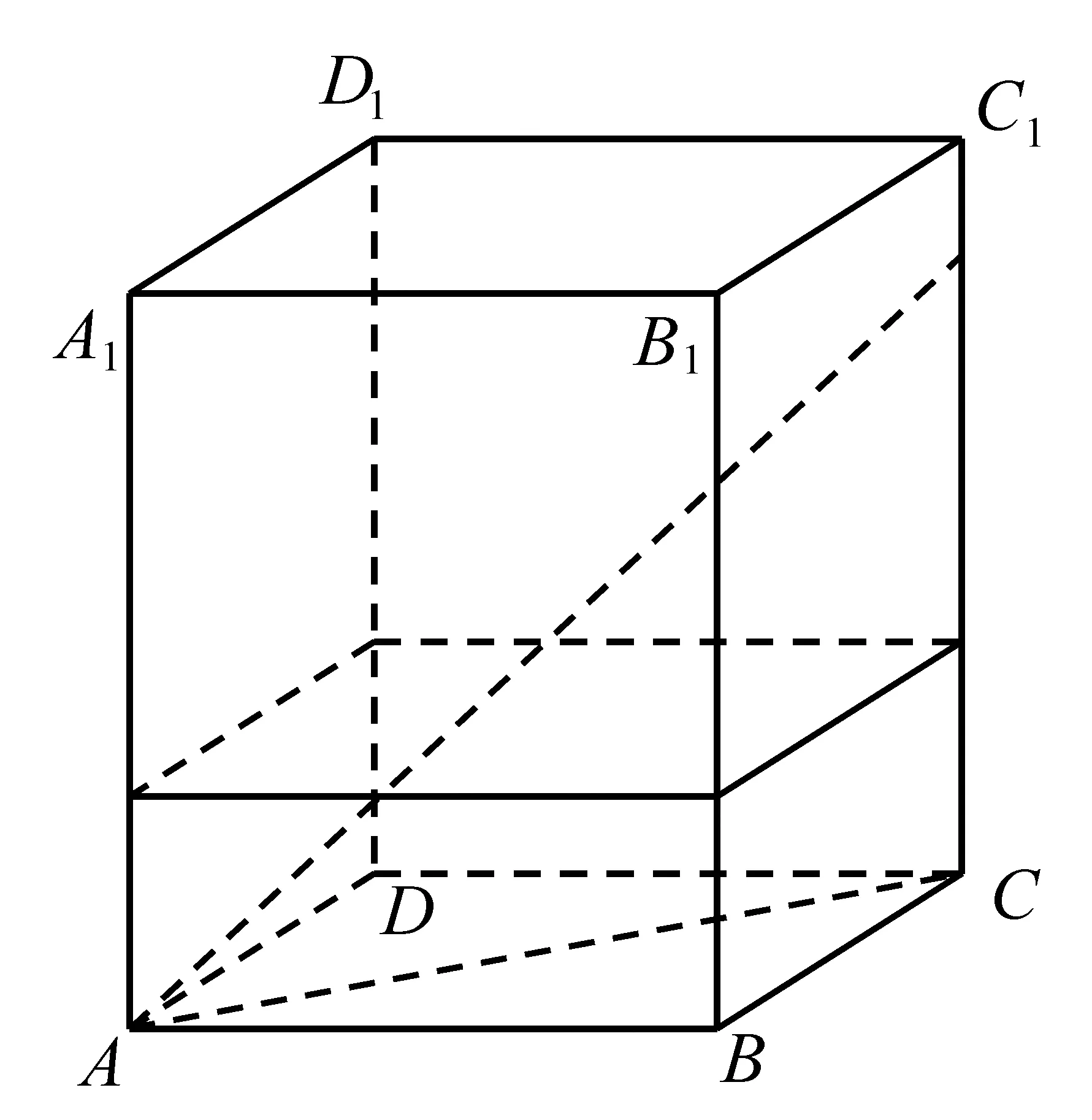
图1

(1)将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；

(2)将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度.

图3

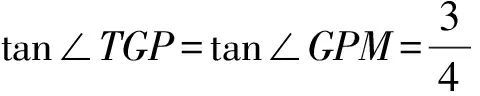
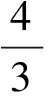
作为命题者，应尽可能预测考生所使用的解题方法.如果少数考生分析能力不强，只能找到了一个不常用的复杂方法，运算很繁，那怨不得人；如果考生是合理分析得到的常用方法，因运算繁琐而不能求解，那就不合适了.运算考查要把准定位，不能让考生因一些机械运算而耗费大量时间，如上文考生想到了不错的方法别解1、2，怎能因一元二次方程的求解，限制考生的正确率呢？其实，只要调整一下等腰梯形上下底与高的长度即可.当然，命题者也许有另外的想法，不想让考生运用别解1，这与高中所学内容关系不大，想重点考查学生三角函数知识的运用，那这道题的设问，应将原没有太大价值的第(1)小题去掉，只考虑正四棱台，增设第(1)小题“求sin∠EGG1”，引导学生运用正余弦定理研究Rt△EGP.一般来讲，试题考查不应限制学生的思路，但短时间内命题，又找不到更好的模型，为防止考生运算偏差，以致运算考查定位不准，不得已而运用的“铺路”命题手段.

2　把控运算时间

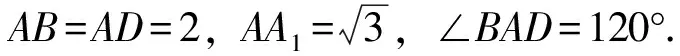
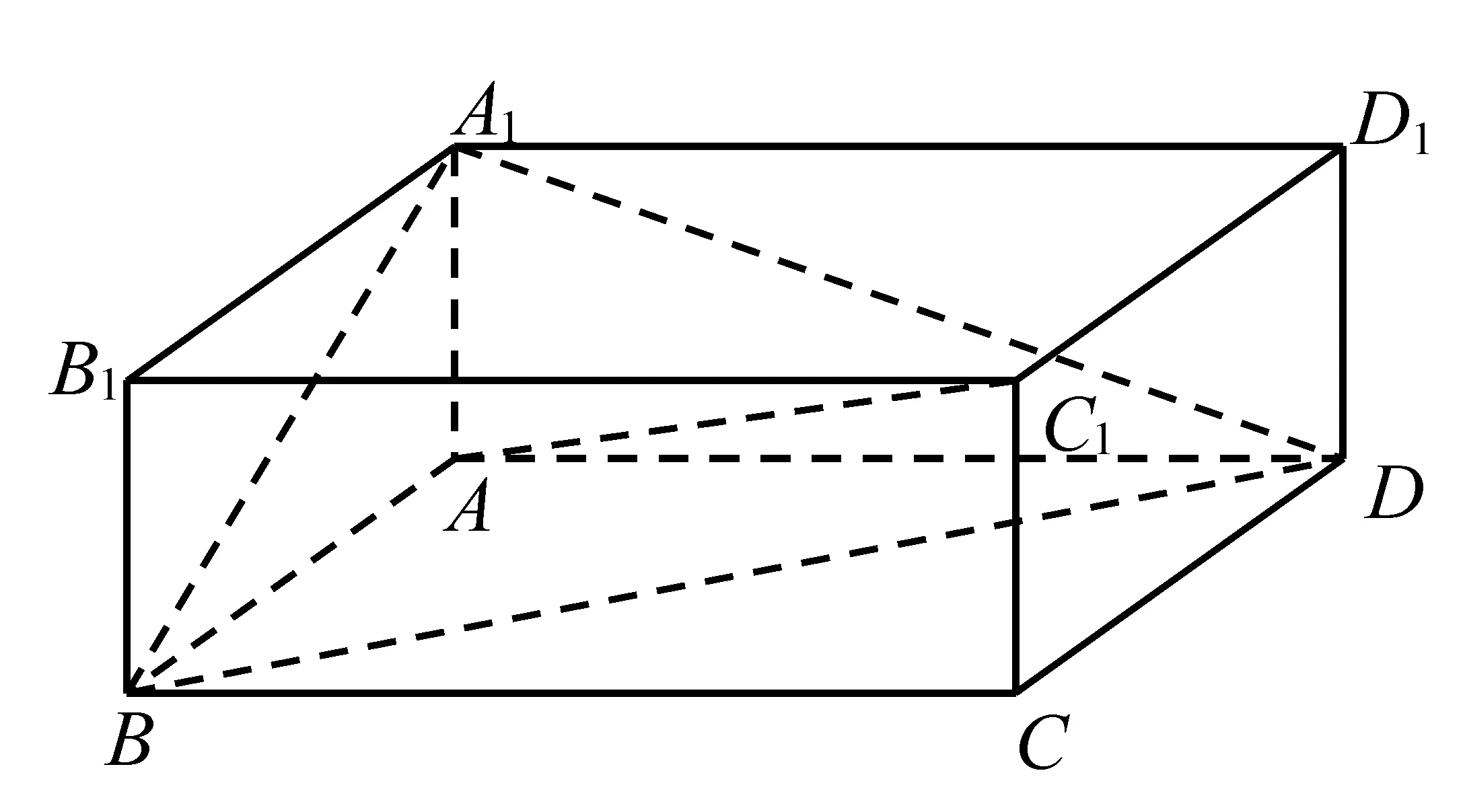
图4

(1)求异面直线A1B与AC1所成角的余弦值；

(2)求二面角B-A1D-A的正弦值.

案例3(2017江苏高考第23题)已知一个口袋装有m个白球，n个黑球(m，n∈N*，n≥2)，这些球除颜色外全部相同.现将口袋中的球随机的逐个取出，并放入如图5所示的编号为1,2,3，…，m+n的抽屉内，其中第k次取球放入编号为k的抽屉(k=1,2,3，…，m+n).

123…m+n

图5

(1)试求编号为2的抽屉内放的是黑球的概率p;

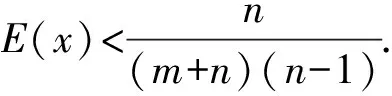
案例2、3是江苏理科附加卷的最后两题，附加卷共3大题，第21题是从平面几何、矩阵与变换、极坐标与参数方程、不等式4道容易题中选2道题完成，时间共计30分钟.笔者觉得总时间有限，运算量不宜过大.一般来讲，第21题4选2大约需要5至8分钟，案例2主要是空间角的运算，考生方法很熟悉，用空间向量的数量积求解，但需要较长时间运算，通常要10分钟左右，完成压轴题的时间肯定不超过15分钟，而案例3需要审题时间，好在这道题的列式不难，但第(2)小题运算技巧强、运算量大，恐怕只有题型熟悉、训练过类似技巧的考生才能完成.笔者总是觉得江苏理科附加卷的时间与题量不匹配，要适当减少一点题量，要让大部分考生有时间思考压轴题，如果考生实在想不到方法，那另当别论；如果很多考生是因为时间不够，而未能思考压轴题，那不合情理.

其实，不只是附加卷要注意控制运算时间，2小时的必做卷也一样，考生要审题时间、要方法的思考时间，整份时间要将运算量控制在合理的范围内，以使绝大部分考生有时间思考每一道题.因此，命题组要关注试卷完成时间问题，特别是试卷定稿，要有完全不熟悉试题的命题成员试做，要能在规定的时间内提前30分钟完成，考试院抽调的命题老师，都是解题高手，他们来不及，大多数考生肯定来不及.

3　淡化运算技巧

4　关注运算程序

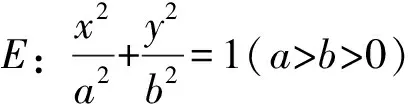
图6

(1)求椭圆E的标准方程；

(2)若直线l1，l2的交点Q在椭圆E上，求点P的坐标.

案例4作为高考题的中档题，其思路方法不难，运算量也不大，笔者没有异议，只是借此说明，解析几何题可变通运算考查要求.以往经常发现一些高考解几题，思路方法灵活多变，运算量也比较大，耗费考生大量时间，得分率也很低.其实，我们可以变通考查要求，强调学生的思维分析能力，关注运算流程，淡化繁难的机械运算，节约考生时间.如案例4的第(2)小题，可要求考生写出解题步骤：

第一步：设P(x0,y0)，并写出直线l1，l2的方程；

第二步：联立直线l1，l2的方程，解出交点Q的坐标；

第三步：将点Q的坐标代入椭圆E的方程，即可求点P的坐标.

当然，对于案例4这样难度的解几题，没有必要只考查运算流程.如果是思路方法灵活多变、运算量又较大的解几题，那么强调思路方法的运算流程的考查，效果就比较好了.问题的设计，可要求考生写出两种(或以上)不同的思路方法，阅卷主要看考生方法的科学性、创新性、灵活性以及运算结果的预见性、运算步骤的程序性等等，由此评价考生，给出合理的得分.我们需要学生有一定能力的运算水平，但没有必要培养他们超强的运算能力，着重思想方法的考查，考生运算程序清晰，就可以！他们将来到高校学习计算机，运算不是问题.

5　杜绝无效运算

案例5(2017江苏高考第20题)已知函数f(x)=x3+ax2+bx+1(a>0，b∈R)有极值，且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)

(1)求b关于a的函数关系式，并写出定义域；

(2)证明：b2>3a;

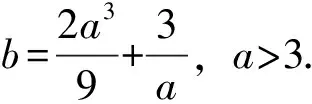
结束语

笔者虽没有参加过高考命题，但多年参加大市调研考试的命题，能体验到高考命题专家的艰辛，为体现高考的选拔性功能，“把关”题要原创，这不是件容易的事，往往是绞尽脑汁！但不管怎么样，我们命题还是要以人为本，站在考生的立场上看问题，“考生的时间来得及吗？，要不要减少试卷的运算量？”、“这道题有哪些方法，考生会不会在某个方法的运算上栽跟头？”、“这是不是运算技巧？考生能算理分析吗？”、“这样的运算考查，有必要吗？”等等.提高高考试卷的科学性、公平性，让考生考出正常的水平，是高考命题要关注的焦点，我们不能因一些运算细节问题，失去试卷的区分度，让一些优生栽跟头，影响他们的终生发展.