基于伪白噪声法的食品缓冲衬垫振动仿真试验

陈 宁 张功学

(陕西科技大学机电工程学院，陕西 西安 710021)

随着社会不断发展，食品的运输量日益增加，食品在运输期间的完整性也越来越重要，减少食品在运输过程中的损坏对经济发展有着重要的影响。在食品运输领域众多学者有着大量的研究，比如邓成江等[1]研究了卷烟工艺中激振的振动松散动体；马涌航等[2-3]对包装材料进行了研究；吴旭填等[4-5]对缓冲衬垫包装性能进行了研究和分析。但对于动力学模型、白噪声激励和食品运输这三者归纳综合研究却很少。食品运输工况同其他物品运输工况相类似，主要是于激励模型建立方法的研究；相比实际测量利用计算机模型相对方便且便于归纳，现主流的运输工况方法有AR模型法[6]、滤波白噪声法[7]和小波包法[8]等。

设计合理的仿真方案不仅可以减少运输系统在实际时间空间的验证，大大缩短食品缓冲材料研发费用及对环境造成的危害，而缩短产品的运输周期，最终达到节约成本促进经济增长的目的。在国内外的研究过程中，大多数对现有的缓冲衬垫及结构设计都采用相关仪器设备进行测试，进而花费大量时间及财力，反之对于虚拟仿真研究则甚少且考虑因素单一。针对该类问题对缓冲衬垫的性能仿真研究十分必要。建立整体的虚拟仿真研究思路，为深入研究和评价食品缓冲衬垫特性有着重要意义。

王文军等[9-10]对不同食品的运输保存做了相关防护保质性试验，其研究重点在于化学防护对食品运输过程中的保鲜，但较少考虑到物理振动过程中影响；巩桂芬等[11]做了力学和结构方面的可行性仿真研究，其重点在于为食品运输过程中的缓冲包装进行结构设计，并进行了包装结构的基本性质测试，但没有将食品的物理特性考虑在内；张功学等[12-14]做了运输条件测试的仿真研究，其研究重点在于对路面激励及运输工具的仿真，没有对货运过程进行仿真试验。本研究使用在车辆运输领域已较为成熟的方法对食品运输过程中的物理振动展开探究，为开展相关综合性研究提供参考。

1 食品缓冲衬垫材料参数

仿真模型分为以某泡沫材料衬垫[15]为运输缓冲模型和以伪白噪声法为运输激励环境模型。在运输缓冲泡沫材料模型中包括有食品缓冲包装和运输工具的刚度系数、质量和阻尼系数的匹配，如果食品缓冲包装材料质量相对较小，可忽略。运输激励环境模型为外部环境对运输缓冲模型的激励，这里采用以泡沫材料制作的方形缓冲衬垫为运输工具，缓冲衬垫的4个支脚分别受到计算机随机产生伪白噪声激励。将随机激励以时域顺序循环代入动力学方程，得到缓冲衬垫在该激励工况下的各项响应结果。在此以被运输食品所受的垂直位移响应着手，通过仿真结果得到相关的激励图，并采用优化结构设计，重新选择衬垫材料等手段为防止发生共振现象做准备。通过仿真得出缓冲衬垫在相应路面激励的共振区间及结合被运输食品的固有频率等特性，降低被运输食品在时域内加速度大于脆值而发生损坏现象。图1为某泡沫材质的缓冲衬垫。根据文献[15]测得相关刚度阻尼系数见表1。

2 衬垫包装系统动力学模型

在衬垫食品包装运输系统中主要是建立运输工具及食品缓冲包装的动力学模型。运输缓冲系统的参数化动力学模型具体是由衬垫和被运输食品组成，在建模过程中以整车模型各部分起缓冲的振动特性的零件为支撑，将其转化为具体的动力学简易模型。

根据缓冲衬垫各支脚在不同激励下运行的状态不同，简化衬垫非阻尼刚度部分，对二轴运输车做如下假设：

① 衬垫在振动过程中基于本体在平衡位置做微小的振幅运动，而且排除变速运动；

② 模型中被运输食品假设为刚体并于衬垫为铰接，不考虑弹性刚度和阻尼性质；

图1 实体泡沫材质的缓冲衬垫结构Figure 1 Cushion structure of solid foam material表1 某实体泡沫材质的缓冲衬垫参数Table 1 Cushion parameters of a solid foam material

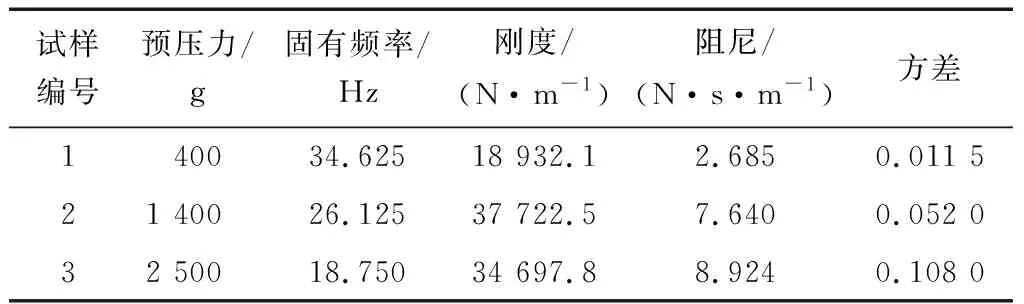
试样编号 预压力/g固有频率/Hz刚度/(N·m-1)阻尼/(N·s·m-1)方差140034.62518 932.12.6850.011 521 40026.12537 722.57.6400.052 032 50018.75034 697.88.9240.108 0

③ 模型中所有支脚接触均为点接触，激励只作用于接触点上过实际平面且垂直向上；

④ 模型中所有简化后的弹簧的满足胡克定律中弹力和弹簧伸缩位移呈线性的要求；

⑤ 模型中所有简化后的阻尼器满足阻尼力由速度的变化而呈现线性改变。

具体食品运输的空间动力学模型见图2。

ma. 被运输物品的质量，2.5 kgmj. 缓冲衬垫包装质量，0.5 kgmjy. 缓冲衬垫俯仰转动惯量，0.75 kg·m2mjx. 缓冲衬垫侧斜转动惯量，0.75 kg·m2m1、m2、m3、m4. 缓冲衬垫4支脚质量，0.1 kgc1、c2、c3、c4. 缓冲衬垫4支脚阻尼系数，8.924 N·s/mk1、k2、k3、k4. 缓冲衬垫4支脚刚度系数，34 697.8 N/me1、e2缓冲衬垫4支脚横向连接点距离，0.20 mf1、f2. 缓冲衬垫4支脚纵向连接点距离，0.15 mxa. 被运输物品的垂直位移，mxj. 缓冲衬垫的垂直位移，mxjy. 缓冲衬垫绕其质心处的纵向角位移，radxjx. 缓冲衬垫绕其质心处的横向角位移，radx2、x4、x2、x4. 缓冲衬垫各支脚的垂直位移，mq2、q4、q2、q4. 缓冲衬垫各支脚受位移激励，m

图2 食品运输的空间动力学模型

Figure 2 Spatial dynamics model of cushioning cushion

3 运输缓冲系统动力学方程建立

根据动力学模型的复杂程度以选择能量法为研究手段，故整车模型动力学中包括3种能量，分别为动能T、势能V和耗散能D，以下围绕这三部分列出整个系统的动力学公式。

整车的动能T为：

(1)

整车的耗散能D为：

(2)

整车的势能V为：

(3)

抓住主要影响因素，忽略不影响或者较小影响，对式(1)、(2)、(3)求导，整理成为经典动力学表达式，见式(4)。

(4)

式中：

[m]——质量矩阵，kg；

[c]——阻尼矩阵，kg；

[k]——刚度矩阵，N·s/m；

[kq]——路面激励矩阵，N/m。

其中：

[k]=

[c]=

k(1,1)=k1+k2+k3+k4,

k(1,2)=-k1e2-k2e2+k3e1+k4e1,

k(1,3)=-k1f2+k2f1+k3f1-k4f2,

k(1,4)=-k1,k(1,5)=-k2,

k(1,6)=-k3,k(1,7)=-k4;

k(2,2)=k1e22+k2e22+k3e12+k4e12,

k(2,3)=k1e2f2-k2e2f1+k3e1f1-k4e1f2,

k(2,4)=k1e2,k(2,5)=k2e2,

k(2,6)=-k3e1,k(2,7)=-k4e1;

k(3,3)=k1f22+k2f12+k3f12+k4f22,

k(3,4)=k1f2,k(3,5)=-k2f1,

k(3,6)=-k3f1,k(3,7)=k4f2;

k(4,4)=k1;k(5,5)=k2;k(6,6)=k3;k(7,7)=k4；

k(2,1)=-k1e2-k2e2+k3e1+k4e1,

k(3,1)=-k1f2+k2f1+k3f1-k4f2,

k(4,1)=-k1,k(5,1)=-k2,

k(6,1)=-k3,k(7,1)=-k4;

k(3,2)=k1e2f2-k2e2f1+k3e1f1-k4e1f2,

k(4,2)=k1e2,

k(5,2)=k2e2,k(6,2)=-k3e1,k(7,2)=-k4e1;

k(5,3)=-k2f1,k(6,3)=-k3f1,c(7,3)=k4f2；

c(1,1)=c1+c2+c3+c4,

c(1,2)=-c1e2-c2e2+c3e1+c4e1,

c(1,3)=-c1f2+c2f1+c3f1-c4f2,

c(1,4)=-c1,c(1,5)=-c2,

c(1,6)=-c3,c(1,7)=-c4;

c(2,2)=c1e22+c2e22+c3e12+c4e12,

c(2,3)=c1e2f2-c2e2f1+c3e1f1-c4e1f2,

c(2,4)=c1e2,

c(2,5)=c2e2,c(2,6)=-c3e1,c(2,7)=-c4e1;

c(3,3)=c1f22+c2f12+c3f12+c4f22,

c(3,4)=c1f2,

c(3,5)=-c2f1,c(3,6)=-c3f1,c(3,7)=c4f2;

c(4,4)=c1;c(5,5)=c2;c(6,6)=c3;c(7,7)=c4；

c(2,1)=-c1e2-c2e2+c3e1+c4e1,

c(3,1)=-c1f2+c2f1+c3f1-c4f2,

c(4,1)=-c1,c(5,1)=-c2,

c(6,1)=-c3,c(7,1)=-c4;

c(3,2)=c1e2f2-c2e2f1+c3e1f1-c4e1f2,

c(4,2)=c1e2,

c(5,2)=c2e2,c(6,2)=-c3e1,c(7,2)=-c4e1;

c(5,3)=-c2f1,c(6,3)=-c3f1,c(7,3)=c4f2。

4 滤波白噪声激励及MATLAB仿真

滤波白噪声在路面激励和汽车虚拟VPG中已被普遍使用，但在衬垫虚拟激励中应用中较少，在此以ISO/TC108/SC2N67标准产生对于缓冲衬垫的空间功率谱密度。常用到滤波白噪声具体表达式：

(5)

式中：

n0——空间原始频率，0.1 m-1；

Gq(n)——激励空间功率谱密度，m2；

n——空间频率，m-1；

Gq(n0)——不平激励系数，m2；

W——频率指数。

(6)

式中：

f——时间频率，Hz；

Gq(f)——时间功率谱密度，m3/Hz；

u——速度，m/s。

因为当n→0时则Gq(n)→0在现实中不存在，故引入空间截止频率nq，通过空间截止频率nq可将式(5)和(6)转化为：

(7)

(8)

(9)

通过MATLAB编程并产生仿真得出高斯白噪声，见图3；随机激励的高斯白噪声和经滤波后的白噪声见图4。

结合之前缓冲衬垫的动力学模型，将滤波白噪声激励频谱于MATLAB软件中进行仿真。由于数据较多，设定步长为500，解得高阶微分方程见图5～7。

图3 高斯白噪声激励Figure 3 Gauss white noise excitation

图4 滤波白噪声激励Figure 4 Filtering white noise excitation

由图5～7可知，以4个随机激励作为衬垫支脚的输入可以得到各支脚的垂直振动位移趋势一致，但在各时间节点会有不同的振幅偏差，其垂直位移的数值<0.007 5 m；衬垫平面两轴向角位移响应大致呈对称式，与测试样品的对称性相关，达到了仿真的效果，该材料在此工况作用下的偏转位移介于0.006 0 rad与0.007 8 rad之间；衬垫平面的垂直位移可以反映该衬垫缓冲性能好坏，被包装物所受垂直位移的响应为0.006～0.007 m，明显小于4支脚的垂直位移量。通过结合运输包装体系的跌落和脆值法对照等综合分析可知，在该激励作用和食品运输系统的减振作用下，被运输食品得到了有效的防护，并且通过线性趋势和实测趋势基本吻合，达到了仿真的效果，验证了在该工况下缓冲衬垫的缓冲特性。

图5 各支脚垂直位移响应Figure 5 vertical displacement of each leg

图6 衬垫平面两轴向角位移响应Figure 6 Cushion plane two axial angular displacement response

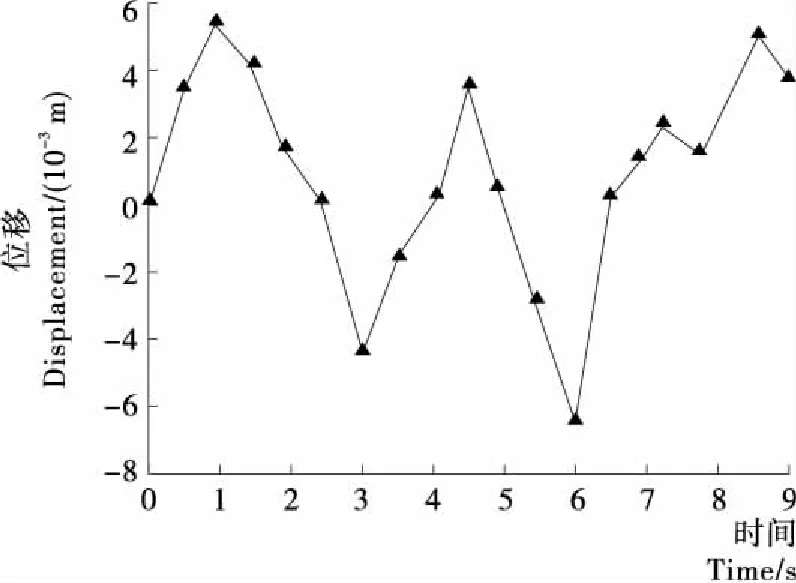
图7 衬垫平面的垂直位移响应Figure 7 The vertical displacement response of the liner plane

5 结论

通过滤波白噪声法模拟食品运输工况中的受激励模型，建立了针对某泡沫材料衬垫的常规七自由度的动力学模型，得到在虚拟激励下食品衬垫系统的垂直位移和偏转角位移响应。

(1) 在该激励作用和衬垫系统的减振作用下，被运输食品的完整性得到了有效保护，并且通过线性趋势和实测相吻合，达到了实操前仿真的目的。

(2) 对多因素综合影响下的食品运输领域仿真提供了创新性的发展，验证了运输动力学在食品运输领域的可行性，可为后续可行性试验操作提供依据。