初中数学最值问题研究与解题策略

陆长蓁

(江苏省扬州市邗江区美琪学校　225100)

一、代数最值解法举例

在生活实践中，人们经常面对带有“最”字的问题，如在一定的方案中，花费最低、消耗最少、产值最高、获利最大等；解数学题时，我们也常常碰到求某个变量的最大值或最小值之类的问题，这就是我们要讨论的最值问题，求最值问题的方法归纳起来有如下几点：

(1)运用配方法求最值；

(2)构造一元二次方程，在方程有解的条件下，利用判别式求最值；

(3)建立函数模型求最值；

(4)利用基本不等式或不等分析法求最值.

1.利用判别式

例1已知四边形ABCD的对角线AC与BD交于点O，若S△AOB=4,S△COD=9,求四边形ABCD的面积最小值.

分析与解答如图1，过A、C作BD的垂线，垂足为F、E，设AF=h1，CE=h2,BD=a,OD=x,则OB=a-x.由已知条件得：

又S四边形ABCD=S△AOB+S△COD+S△BOC+S△AOD=S△BOC+S△AOD+13.

于是求四边形ABCD面积最小值问题转化为求S=S△BOC+S△AOD最小值问题.

(13+S)x2-(18-S)ax+9a2=0(3)

若方程(3)有实数根，必须有

Δ=a2(18+S)2-36a2(13+S)=a2S2-144≥0.

而a>0,从而a2>0，于是必须S2-144≥0，因为S>0，所以最小值S=12.从而S四边形ABCD最小值为25.

2.运用函数思想

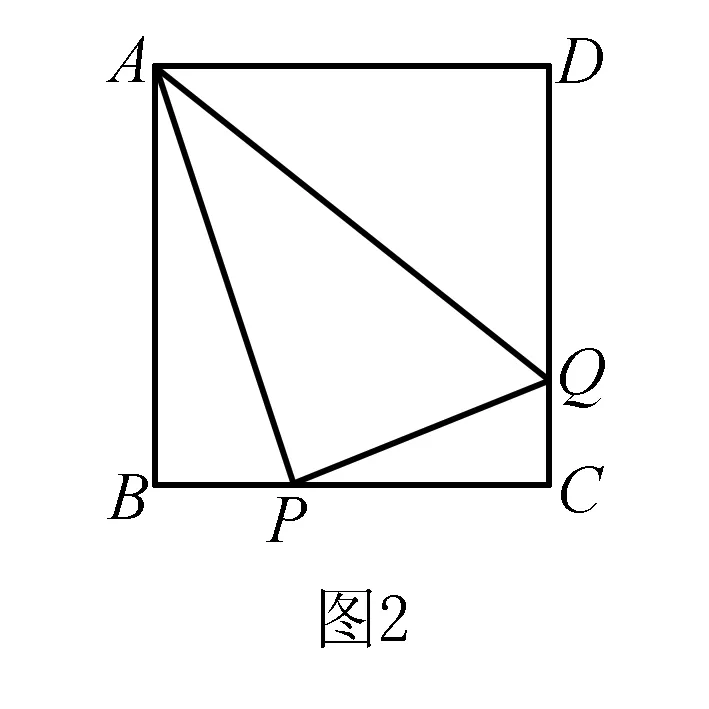
例2如图2，正方形ABCD的边长为4，P是边BC上一点，QP⊥AP交DC于Q，问当P在何位置时，△ADQ的面积最小？并求出这个最小值.

分析与解答根据作图实验可知，随着P点在BC上运动，Q点将在BC上运动，但在运动过程中△ABP与△PCQ始终相似，因此可利用相似三角形的性质表示出△ADQ的面积与BP之间的函数关系式，从而可进一步求解.

由二次函数得性质可知，当x=2时，y有最小值，最小值是6.即当P点在BC的中点时，△ADQ的面积最小，最小面积是6.

3.利用整数的奇偶性

例3一个直角三角形的三条边的长均为整数，已知它的一条直角边的长是18，那么另一条直角边的长有____种可能，它的最大值____.

分析与解答设直角三角形的直角边是a，斜边是c，由勾股定理可得c2=a2+18a2，移项，因式分解，得(c+a)(c-a)=182.因为c、a是正整数，所以c+a>c-a，且c+a与c-a的奇偶性相同，又182是偶数，故c+a、c-a必同为偶数.又(c+a)(c-a)=182=22×34=(34×2)×2=(33×2)×(3×2).

所以另一条直角边有两种可能，它的最大值是80.

二、几何最值解法举例

几何最值问题在初中数学中经常遇见，由于它涉及的知识面宽，灵活性大，综合性强，结构新颖，因而有利于考查学生的思维能力和创新意识，一直是中考和各类数学竞赛的热点之一.为帮助同学们掌握此类问题常见的解题策略，现举例如下.

1.利用对称变换

例4如图3，正方形ABCD的边长为3，点E在BC上，且BE=2，点P在BD上移动，则PE+PC的最小值是多少？

分析与解答要求PE+PC的最小值，即在直线BD的同旁有E、C两点，在BD上找一点P使PE+PC最小，可以通过对称变换，将PC变换后求解.

2.利用面积

例5如图4，正方形ABCD的边长为1，P为BC边上任意一点，分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，求BB′+CC′+DD′的最大值或最小值.

分析与解答正方形ABCD是确定的，线段BB′、CC′、DD′的长度随P的位置的变化而变化.BB′、CC′、DD′分别是△ABP、△ACP、△ADP中AP边上的高，若运用几个三角形面积的和的关系，可将求BB′+CC′+DD′的最值问题转化为为确定AP的最值.

连结AC、DP.

∵ABCD为正方形，且边长是1，且S△ADP=S△ADC.

3.利用几何图形特性

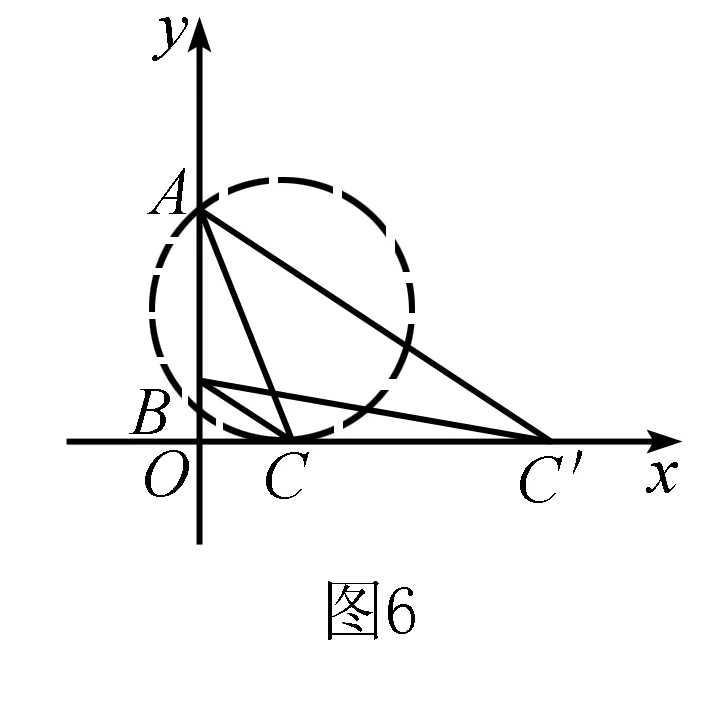
例7如图5，在平面直角坐标系中，在y轴的正半轴上(坐标原点除外)，给定两点A(0，a),B(0,b)(a>b).试在x轴的正半轴上(原点除外)求出点C，使∠ACB取得最大值.

分析与解答考虑到圆周角的特性：“在同圆中同弧所对的圆周角相等，且大于这条弧所对的圆外角小于这条弧所对的圆内角.”因此在过A、B两点的所有圆中必有一个圆与x轴的正半轴相切，这个切点即为所求的点C，如图6.C点的坐标可通过切割线定理求得.

以上几例介绍了求最值的基本方法，他们具有一定的代表性.在学习中同学们要不断地积累，归纳和总结，灵活地掌握和运用.