基于系统动力学模型的工业生长指数参数化模拟研究1

徐 健

（华南理工大学 经济贸易学院，广东 广州 510640）

1　引言

伴随着我国制造业的粗放式膨胀扩张，整体环境恶化已为人共知，工业园区的景观设计及规划也一直被从设计角度一再提及，但工业园区的总体实际景观比例和环境、景观设计的主观评价却鲜被关注.工业与环境的关系的研究始于Weber［1］的工业区位理论，经过Losch［2］等的工业生命循环阶段论和区域经济发展梯度转移论，止于Krugman［3］的空间经济模型.经过一些学者线性预测和从神经网络的挖掘［4］，对工业生长的研究目前一直处于定性分析提出策略的角度，至今仍缺乏一种工业与环境之间的整体模型对工业生长与环境及景观生态的矛盾关系进行规划指导.目前也没有基于景观生态实际量化关系对工业与景观生态用地发展的参数化模拟.

系统动力学方法基于定性分析，通过筛选系统因子将因子间逻辑关系写入程序流图，将数据带入可以量化的有预测、调试功能的系统动力学模型Vensim软件平台中进行仿真模拟，其结果具有很强的符实性、可靠性，擅长处理长期性、高阶、非线性、时变性的多元反馈问题，在处理社会经济问题时显示出了其他方法无可比拟的优越性.本文旨在通过建立工业生长—景观生态系统动力学模型和参数化模拟对城市基于平衡景观生态保护和工业发展的关系进行性可持续性规划提供建议.首先通过环境评价和景观元素构成比例揭示了工业发展对整个系统的影响，确立了模型架构及五个子系统间的关联特征以哈尔滨为例训练并验证了系统动力学模型，进而将量化关系进行编程导入Grasshopper对工业生长指数进行参数化三维模拟，对比模拟结果和哈尔滨市现有规划提出建议.

2　模型因子分析

为了解城市工业园区实际环境情况，并明确工业发展与城市体系的内在联系，找到城市工业发展的主要影响因子和相关联系，本文在全国范围内随机抽取9个工业园区进行270份环境问卷调查［5］.结果显示，空气、水和噪声污染满意度最低；受访者通过植物覆盖程度和动物生存迁徙情况评价表达了对绿化廊道和生态廊道的连通度的不满；在城市经济方面，公众对景观设计评价均为不满意，其中水景设计及应用最低；在体育活动设施方面，公众对康体设施的建设表示不满，但是对休闲广场表示满意；在公众的主观感受方面，工业城市中的人们普遍觉得舒适和安全；公众呼唤减慢工业建设速度以减轻环境污染和恢复景观生态，并有很强的与政府配合意愿和个体奉献精神.问卷结果体现了工业城市快速发展已经导致了严重的环境污染和景观生态破坏，当地民众呼唤政府参与性的控制与能协调景观生态和工业发展的可持续性规划.

为全面考虑客观环境对主观问卷结果的影响，对采访园区进行了视频采集，经过校正景深以及天空比例和MATLAB中值滤波处理后，将视频每十帧截取一幅分解成若干图片（1280*720，JPG）.进而通过定义三种主要景观元素在图像中的颜色阈值计算工业、景观绿化、公共设施像素各在视频中所占比例，得到主观评价和景观像素比例之间的相关性.

综上，将主观评价结果进行相关性统计，结合客观景观构成比例得出工业生长、环境污染、景观生态、发展和政策与包括主观感受、景观设计、体育活动设施在内的城市经济体系之间的联系依据，建立出工业城市系统因果关系框架，如图1所示，为工业城市系统动力学的模型建立了主观与客观交叉的量化关系基础.

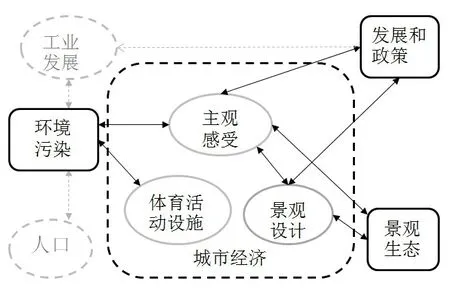
图1　城市工业生长系统因果关系流图

3　建立系统动力学模型

应用系统动力学方法实现工业与城市其它体系之间的相对闭合量化模型，较传统数学模型更能充分反映系统的非线性结构和动态变化，完成从定性到量化的转变.结合以上问卷及调研分析结果，并借鉴工业区域经济理论［1］及Wrigley等对工业区和人口变化关系的研究［6］及Pargal等对发展中国家的工业污染环境研究［7］等理论成果，本研究将整个体系分解为企业子系统、城市经济子系统、人口子系统、环境子系统、景观生态子系统.将调查问卷公众评价相关性结果及三种景观像素与问卷结果的相关性结论融入图1因果关系流图，生成了工业城市系统动力学子系统关系模型框架图，如图2所示.

哈尔滨从建国初期就是中国的工业基地，在过去的几十年工业发展迅速而目前却遭遇景观生态制约而陷入瓶颈停滞不前，具有研究典型代表性［8］，其社会基础数据完备且卫星图像清晰连续，具有研究可行性.因此，本文以哈尔滨为例，统计其2000-2010年社会、经济、人口、数据应用主成分分析和因子分析相结合约减变量的方法结合文献理论综述最终遴选出各个子系统的主要影响因子，确定子系统中的水平变量和速率变量.

图2　城市工业生长—景观生态系统动力学模型框架图

为避免工业系统无尽的向外扩张，系统设定以下边界：在工业子系统量化中，以政府年鉴中列入的大中规模企业数量计算；环境子系统因子取值按历年工业污染所占各项环境污染加权平均比例值进行计算；在以上限定下，分析主要影响因子间的因果关系用Vensim DSS建立工业城市系统动力学总模型，如图3所示，应用2005-2015年数据将模型训练使其平衡.

图3　工业生长—景观生态系统动力学总模型

由于Vensim软件的公式编辑限制导致的误差必然性［9］，模型进行历史数据检验和未来预测检验.选择2005-2015年所有系统因子与系统实际运行值相比较，全部因子平均误差率为2.96%；对模型进行未来模拟测试得到2010年模拟数据数据与实际数据相比误差为3.29%，在误差允许范围5%以内［10］，证明了模型的可靠性和有效性.

应用本模型可以对其它状态变量（如工业、人口、环境污染投资等）进行多种发展方案假设模拟，根据模型输出变化观察景观格局指数的动态变化趋势和范围，从而保持工业建设和城市经济发展、人口迁徙及环境污染、景观生态的平衡，从宏观上指导城市工业的可持续发展［11］；模型应用灵活，可以简化和变形及增加因子对多种问题进行假设模拟，例如，增加“城市分布形态”因子，使系统在不用城市形态下重新平衡，即可通过模拟比较分析不同城市分布模式下，城市景观生态风险性的不同［12］.还可以通过系统因子之间的关系发觉系统之间的量化关系，将其间的数学关系倒入可视化参数化模型，使量化关系变成可视化参数化模型，从而实际指导城市工业用地规划布局.

4　系统动力学的应用及参数化模拟结果

Grasshopper通过方案逻辑结合编程指导建模过程，可以通过参数的调整直接改变模型形态，完成从量化到形态化模拟的转变［13］.目前，哈尔滨在老工业基地复兴进程中面临工业生长和景观生态保护的矛盾，单纯系统动力学模型模拟结果不足以完整的指导具体工业发展方位性规划.因此，研究将量化转化为立体模拟，以点、线、面的路径对栅格（栅格为200*200m）内圆柱的高度影响模拟不同用地分类对周围用地工业生长指数影响，经过对电池组进行逻辑梳理和系统编程将量化关系在平面上“生长”出符合区域景观生态可持续性发展的哈尔滨工业生长曲面.

4.1　逻辑关系

根据工业生长—景观生态系统动力学模型（见图3）的各种用地关系得出各种用地斑块与工业用地之间的数学回归关系，如图4所示.经定性分析结合量化结果得出各种用地类型斑块对生产用地斑块的生成刺激、屏蔽及削弱的逻辑关系，如图5所示，建立参数化模拟的逻辑基础.

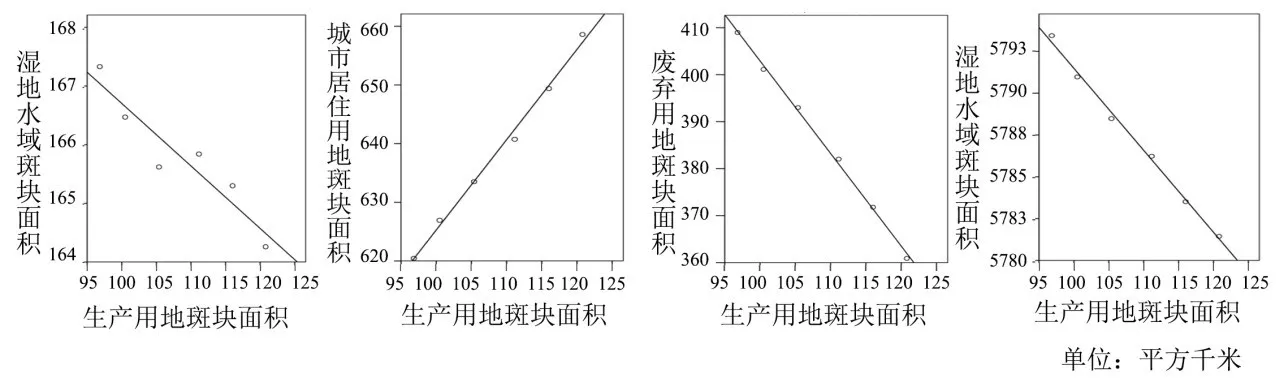
图4　各种土地类型与工业用地之间的数学回归关系

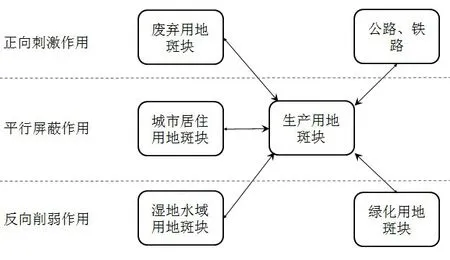
图5　各种土地类型与工业用地之间的逻辑关系

4.2　程序设定

由以上数学关系推演得到中的各种用地斑块对哈尔滨边界内的土地栅格工业生长指数（I）公式，如表1所示，公式的设定决定了最后的模拟效果.

表1　各种用地斑块对边界内工业生长指数影响类型及公式

4.3　参数化模拟结果

在城市景观生态与工业生长可持续平衡发展的前提下，为保证各种用地类型的镶嵌关系和绿地廊道的连续性，参数化模拟应在景观异质性指数在0.72-0.78和绿地景观联通度为0.35-0.39取值范围下进行（景观指数变化范围不超过系统动力学模型试验极限值的5%，如超过此范围Grasshopper中的公式因打破了系统平衡需重新设置）.其模拟结果如图6所示，a、b、c、d、e依次代表废弃用地、公路和铁路、城市居住用地、绿化用地、湿地水域用地对边界内的其他用地工业生长指数的影响，其影响强度和范围平面图如图6（a-e）-1所示；其影响的强弱以地块栅格内圆柱高度的代表，如图6（a-e）-2、6（a-e）-3以两个方向的鸟瞰图展示参数化立体模拟的结果.

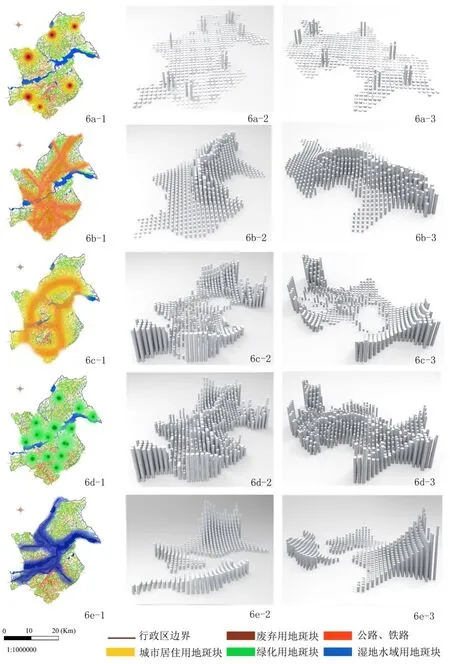
图6　各种用地对工业生长指数的影响演示及立体模拟效果

如图7所示，将各种用地对边界内土地工业生长指数的影响融合，在Grasshopper中进行效果叠加得到所有用地类型对哈尔滨市的工业建设指数分布图.如图7-1所示，栅格所对应的柱状高度代表此地块的工业生长指数，即柱形高度越高越该地块越适合发展工业.将柱状顶点连接成网状结构（如图7-2所示），再将网状结构渲染成面（如图7-3所示），对其进行进一步参数化设置，从景观生态保护的角度设定景观异质性指数和绿地联通度求取系统运行均值的情况下，如图7-4所示，图中绿色部分均为不适合发展经济的地区，灰色部分为可以进行工业开发的区域.

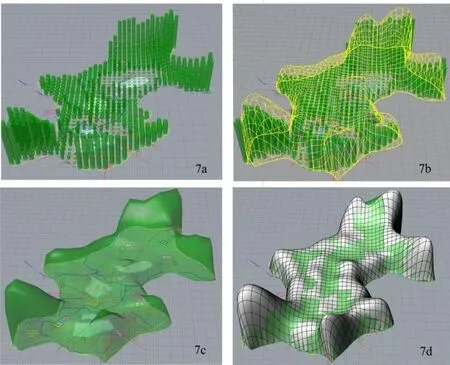
图7　多种因素共同作用下的哈尔滨工业生长指数曲面

将此模型对应哈尔滨实际的用地分类图即得到哈尔滨具体工业生长开发曲面，可观测到各栅格所对应的工业生长指数，如图8a所示，对比哈尔滨现有城市工业开发规划（2011-2020年）如图8b所示［14］，分析可以得到政府规划发展的工业用地的工业生长指数情况.

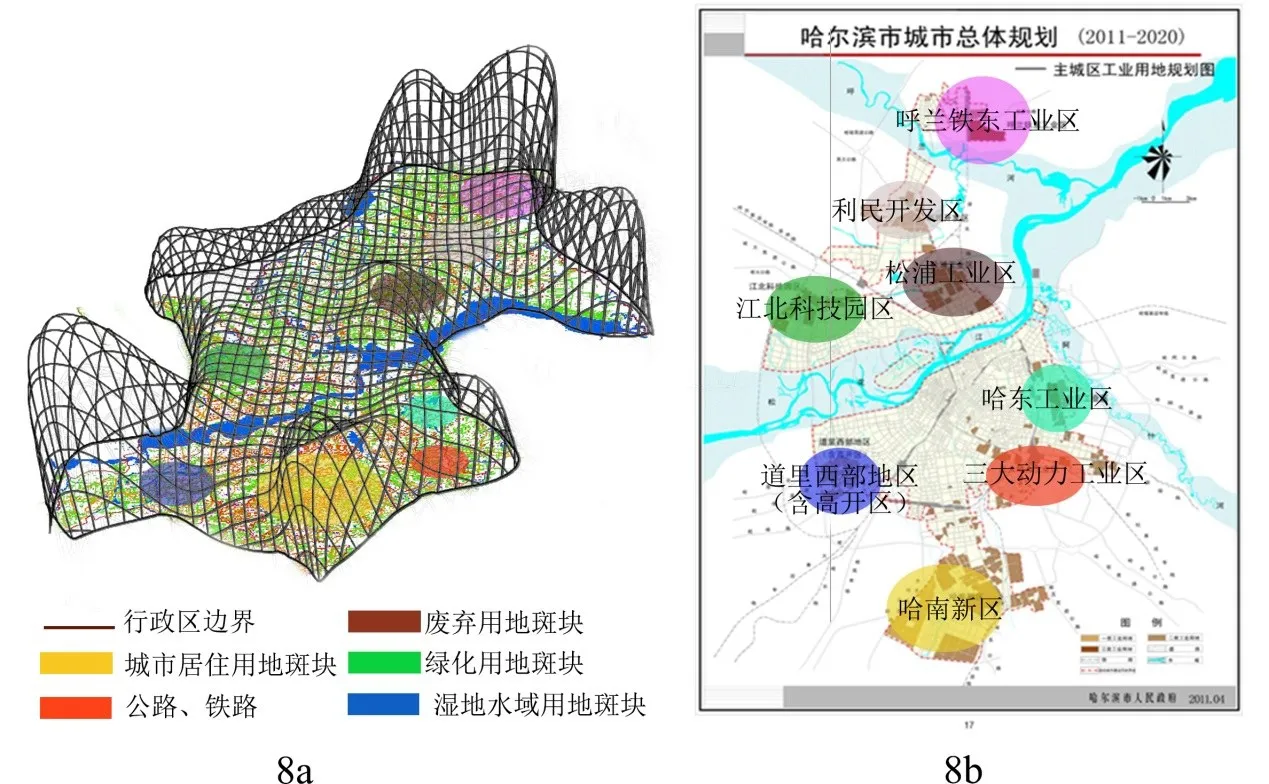
图8　基于景观生态保护的哈尔滨市工业生长指数曲面和（2011-2020）工业用地规划对比图

基于以上分析，得出对原有工业发展规划的两点建议：

（1）根据本文研究结果，哈尔滨的工业开发重点依次为呼兰铁东工业区、哈南新区、松浦工业区、哈东工业区、利民开发区、道里西部地区（含高开区）、江北科技园区和三大动力工业区，投资次序应按工业生长指数次序排序.

（2）基于城市景观生态学保护理论，道里西部地区（含高开区）、江北科技园区和三大动力工业区地理位置不适于作为大面积工业开发用地，如强制开发将对哈尔滨城市生态体系健康有不良影响.如必须对其进行工业建设，应限定产业类型，如绿色食品基地、科技合作基地等环境污染小的产业类型.

5　结语

本文通过主观问卷调研发掘城市工业和城市各系统间的关系，进而建立了城市工业生长—景观生态系统动力学模型.根据模型得到基于景观生态保护的各用地之间的量化关系，应用Grasshopper编程生成了基于景观生态保护的工业生长指数参数化三维模型.本研究将景观生态与社会发展相联系，实现了从理论到量化，从量化到动态形象化转变.工业生长曲面可以直观表达基于景观生态保护的规划用地的工业开发适宜度，根据曲面的高度指导工业开发的用地走向，使经济发展和景观生态及环境保护找到了一种可持续的平衡发展模式.规划决策者可以根据此模型对现有规划方案进行补充及校正，也可以对未来规划进行有效理论指导；另外，通过对系统动力学模型内的因子进行方案假设，如模拟人口、企业激增或锐减模拟，政府环保投资力度模拟，盐碱地绿化模拟等，既可以通过系统动力学的重新平衡得知经济、社会、环境、生态各子系统变化，又可由新的量化关系参数化模拟工业生长曲面的形态，对城市长期规划发展有着实践指导和理论模拟的双重意义.