论均质半圆环 半圆盘 半球体质心的求法

刘 红

(重庆市第一中学校　重庆　400030)

高中物理研究的物体一般可以看作质点，所谓质点就是有质量但不存在体积或形状的点，是物理学的一个理想化模型．物体的实际运动往往要复杂得多，我们要研究这个物体的整体运动，就只需找到这个物体的质量中心即质心(质心，指物质系统上被认为质量集中于此的一个假想点)的运动即可．物体任何一部分的运动一般都可分解为质心的运动和物体的该部分相对于质心的运动，如图1所示的跳水运动员的运动就是如此．

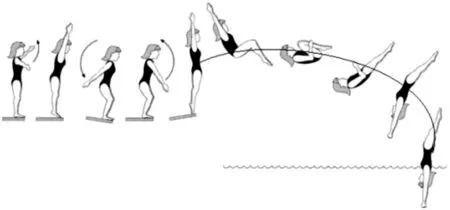
图1　跳水运动员的运动

多个物体组成的质点组中任何一个物体的运动一般都可分解为质点组质心的运动和该物体相对于质点组质心的运动．所以求物体或质点组的质心就显得特别重要．在对学有余力的高中生进行物理竞赛培训时，就会涉及到求物体的质心．

本文就均质半圆环、半圆盘、半球体质心的求法做一些探讨，以期在这方面有一点作用．因为面对的是中学生，所以微元的选取只限于一维情况．

1　质心的定义

如图2所示的物体组，参考位置为O．

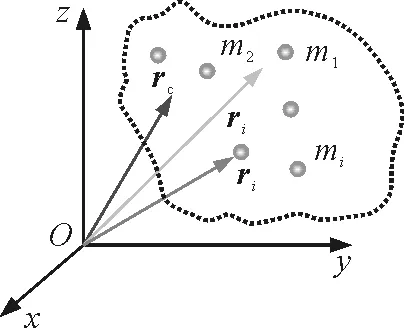
图2　质心的定义

2　巴普斯定理

(1)在一平面上取任一闭合区域，其面积为S，使它沿垂直于该区域的平面运动形成一个体积为V的立体，那么这个立体图形的体积就等于质心所经路程r乘以区域面积．表达式为V=Sr．

(2)设某一长为L的曲线段，让它沿着垂直于它所在平面的方向扫过一个面积S，那么这个面积的大小就等于线段的质心移动的距离r乘以线段的长度．表达式为S=Lr．

【例1】已知半圆环质量为M，半径为R．求它的质心位置？

方法一：巴普斯定理

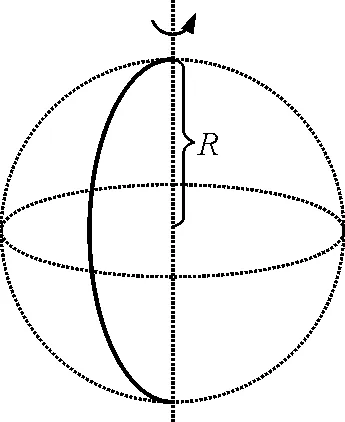
图3　半圆盘绕直径360°形成空心球

方法二：旋转法

据半圆环的对称性知它的质心在对称轴上，设质心距圆心距离为r．让半圆环绕它的直径在半圆环平面内转过一个极小角度Δθ(Δθ→0)，如图4所示．

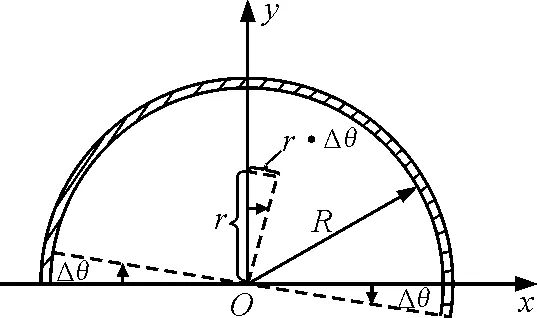
图4　半圆环转过一个极小角度

xc=r·Δθ=

代入

就得

方法三：微元法

据半圆环的对称性知它的质心在对称轴上，即在图5的y轴上．设质心距圆心距离为r(即yc=r)．

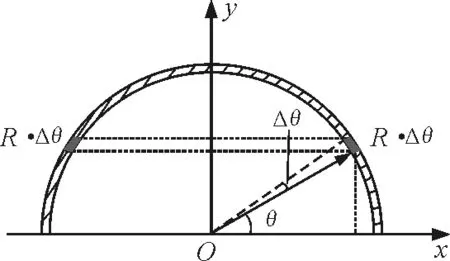
图5　质心在y轴上

半圆环上任意一点的坐标

x=Rcosθy=Rsinθ

半圆环上微小长度为R·Δθ，设半圆环单位长度的质量为λ，则

据质心的定义有

所以

代入

可得

【例2】已知半圆盘质量为M，半径为R．求：它的质心位置？

方法一：巴普斯定理

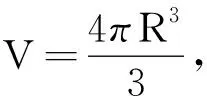
得到

方法二：等效半圆环

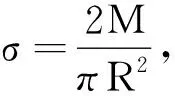
图7

代入

可得

方法三：微元法

半圆盘可以看成有无数多个矩形组成，如图8所示．半圆盘边沿上任意一点的坐标x=Rcosθ,y=Rsinθ．

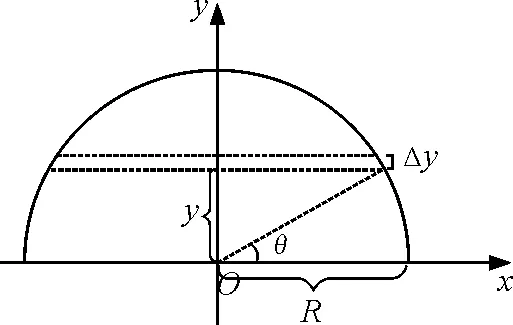
图8　半圆盘可看成无数个矩形组成

又因为

Δy=Δ(Rsinθ)=Rcosθ·Δθ

所以

代入

就得

【例3】已知半球质量为M，半径为R．求：它的质心位置.

方法一：巴普斯定理

图9　半球等效

据质心的定义即可求出半球的质心

所以关键就在求圆锥的质心．

设圆锥的质心距其底面的距离hc，如图10所示．圆锥的底面向下移动微小距离Δh(Δh→0)，据质心的定义和圆椎体质心的相似性知

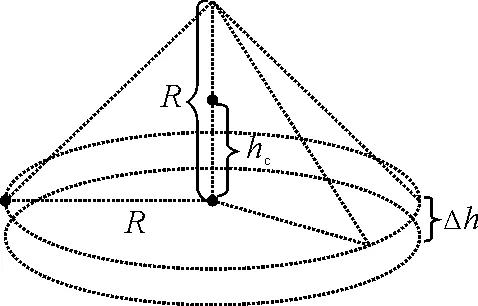
图10　圆锥质心距底面hc

可求出新圆锥体的质心

化简得

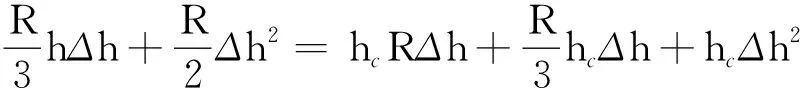
又因为Δh→0，略去二阶小量，所以

代入得半球的质心为

方法二：微元之圆柱法

半球可以看作是由无穷多个圆柱组成，如图11所示．

图11　半球看成无穷多个圆柱

据对称性可知质心在对称轴上，据质心的定义有

所以

方法三：微元之球壳法

半球体可以看作有无穷多个半球壳组成，如图12所示．

图12　半球体看作无穷多个半球壳

只要知道半球壳的质心位置，就可求得半球的质心位置．设半球壳的面密度为σ，半球壳可以看作有无穷多个矩形组成，如图13所示．

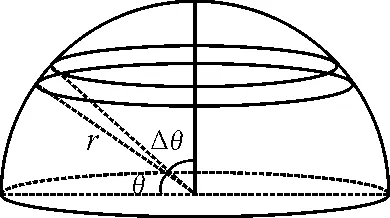
图13　半球壳看作无穷多个矩形

据质心的定义知半球壳的质心位置

设半球的体密度为ρ，则据质心的定义知半球的质心位置

通过对半圆环、半圆盘、半球体质心多种求法的讨论，打开了学生的思路，展示了微积分处理问题的思想方法，体现了数学、物理知识的融合，为学生以后解决更复杂的物理问题奠定了基础．