值得举一反三的一维阶梯势问题*
2018-07-13陆爱江杨沁玉
陆爱江 杨沁玉
(东华大学理学院物理系 上海 201620)
在《量子力学》课程中一维定态问题是一个教学的重点.它是学习量子化概念的基础,也是学生初次接触薛定谔方程,对量子概念有所体会的生动范例.我们在课堂上对很多基本的一维势阱、势垒问题做出了细致的讲解和计算,也有很多同仁对这些问题进行讨论[1,2].而对这一类问题——一维阶梯势问题[3,4],我们却较少关注.此类问题在习题中、考研试卷中偶尔出现[5,6],考查学生求解一维薛定谔方程的基本技能.一维阶梯势的问题不是一个特殊的问题,但是在与学生的讨论和教学中我们发现,这是一个值得认真研究的问题.
1 高于零点的阶梯势 且粒子能量E>V0
1.1 粒子从左侧入射
首先我们来看看教材中的习题设计[7].首先,一维阶梯势的势分布以分段函数形式给出 ,如图1所示.

图1 高于零点的一维阶梯势分布
(1)
假设粒子(能量E>V0)从左侧入射,求解反射系数和透射系数.
规范的求解步骤如下.
(1)写出薛定谔方程
(2)
(2)对不同区域求解
I区
(3)
ψI=Aeikx+Re-ikx
(4)
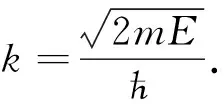
II区
(5)
ψII=Teik′x
(6)


(7)
进而得到反射系数为
(8)
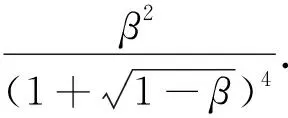
对这个结果我们可以讨论两种极限的情况.β≈0时(几乎没有阶梯或者粒子能量远大于阶梯势的高度),反射系数趋近于零,粒子完全通过;β≈1时(粒子能量与阶梯平齐),反射系数趋近于1,粒子被完全反射,即粒子没有机会进入到右侧区域(Ⅱ).
1.2 粒子从右侧入射
如果粒子(能量E>V0)从右侧入射,情况会不会不同呢?
(9)
ψⅡ=Ae-ikx+Reikx
(10)


(11)
ψⅠ=Te-ik′x
(12)



(13)
反射系数为
(14)
仔细观察,上述结果式(14)与粒子从左侧入射的结果式(8)完全相同.这个结果是不是令人感到惊奇?
可能很多同学在求解1.2问题之前,会想当然地认为,从左侧入射的情况反射系数应该大于从右侧入射的反射系数.这实际上是一个宏观的印象——人在行走中上下台阶的困难程度是不同的.而实际上严格的求解告诉我们,在量子的范畴,阶梯势对粒子的反射几率是同一的,不论粒子从哪一侧入射.这一结果恰恰体现了量子世界的与众不同.通过对这个题目的详细求解应该会让同学们对量子力学这门课程的独特之处有一个更直接的体会.
2 高于零点的阶梯势 且粒子能量E细心的同学会注意到,我们在解决上面问题时要求粒子的能量E>V0,那么如果粒子能量不满足这个条件,其结果又会怎样呢?我们假设粒子从左侧入射,V0>E>0,薛定谔方程可以写为

(15)
ψⅠ=Aeikx+Re-ikx
(16)

(17)
ψⅡ=Te-k′x
(18)

零点处连续,所以
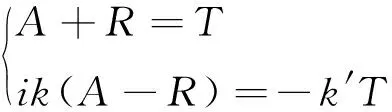
解得
反射系数为1.
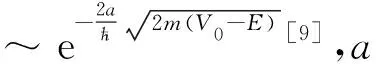
3 低于零点的阶梯势
我们还看到很多习题中的一维阶梯势是这么给出的
(19)
如图2所示.

图2 低于零点的一维阶梯势分布
假设粒子(能量E>0)仍然从左侧入射,求透射系数和反射系数.
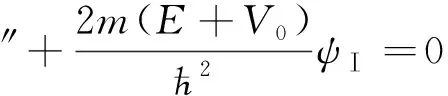
(20)
ψⅠ=Aeikx+Re-ikx
(21)

(22)
ψⅡ=Teik′x
(23)

所以连续性条件给出

反射系数为
(24)
如果V0=βE(0<β<1),反射系数即为
(25)
当β≈0时(几乎没有阶梯或者粒子能量远大于阶梯势高度),反射系数趋近于零,粒子完全通过;E≈0时(相当于β→∞),反射系数趋近于1,粒子被完全反射,即粒子没有机会进入到右侧区域(Ⅱ).实际上,当能量E<0,粒子都将被完全反射,情况与2中的例子相同.
有的同学可能会对这一结果产生疑问.坐标的选择完全是人为的呀,为什么我们把坐标轴向上移动了V0而已,反射系数的表达式就有所不同了.粒子能量与势的关系均为V0=βE,其散射结果难道不应该是相同的吗?这里可能大家忽略了一个细节——考虑两种不同情况下粒子以相同能量E入射:从经典的观点考虑,当阶梯势高于零点,粒子的动能在x>0的区域为E-V0,而在x<0的区域为E;而当阶梯势与零点平齐,粒子的动能在x>0的区域为E,在x<0的区域为E-(-V0)=E+V0.也就是说以相同能量入射的粒子,在这两种势分布下,在x>0的区域其动能分别为E-V0和E,在x<0的区域,其动能分别为E和E+V0.所以,从能量零点选取的角度考虑,一种情况下入射能量为E对应另一种情况下入射能量为E-V0的情况.当入射粒子能量与阶梯势的相对关系一致时,所得的结果才会相同.
由一道简单的一维阶梯势的问题,我们竟然可以得到这么多有趣的结果.这也启发我们对很多《量子力学》中的问题需要举一反三.我们传统的课堂讲授内容可能更偏向于横向的比较,比如一维无限深势阱、一维有限深势阱、一维谐振子……而对问题的纵向延伸做得不够.这样做的结果是,同学们对老师课堂讲的例题能听懂,但是自己做习题就完全无从下手.此文中这样的举一反三既可以增加一点课程的趣味性,也能够激励学生思考,对学过的内容提出新的问题,这就是培养学生研究能力的一个有益模式.
IssueofOneDimensionalStaircasePotentialWorthyofInferingOtherThingsfromOneFact
Lu AijiangYang Qinyu
(Science College,Donghua University,Shanghai201620)
Abstract:Based on the quantum mechanics problem with one dimensional (1D) step-like potential, many an interesting results have been obtained.The moving directions of the injected particles and the position of the step-like potential are attributed to the main facets of this problem.It is a good exercise about 1D stationary state,and is a typical problem to show the specialty of quantum mechanics.
Keywords:step-like potential;potential function;transmission coefficient;reflectance
细心的同学会注意到,我们在解决上面问题时要求粒子的能量E>V0,那么如果粒子能量不满足这个条件,其结果又会怎样呢?我们假设粒子从左侧入射,V0>E>0,薛定谔方程可以写为

(15)
ψⅠ=Aeikx+Re-ikx
(16)

(17)
ψⅡ=Te-k′x
(18)

零点处连续,所以
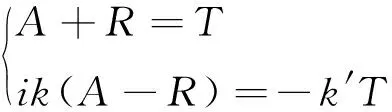
解得
反射系数为1.
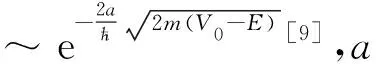
3 低于零点的阶梯势
我们还看到很多习题中的一维阶梯势是这么给出的
(19)
如图2所示.

图2 低于零点的一维阶梯势分布
假设粒子(能量E>0)仍然从左侧入射,求透射系数和反射系数.
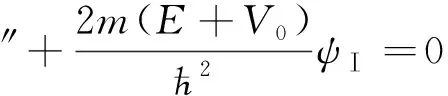
(20)
ψⅠ=Aeikx+Re-ikx
(21)

(22)
ψⅡ=Teik′x
(23)

所以连续性条件给出

反射系数为
(24)
如果V0=βE(0<β<1),反射系数即为
(25)
当β≈0时(几乎没有阶梯或者粒子能量远大于阶梯势高度),反射系数趋近于零,粒子完全通过;E≈0时(相当于β→∞),反射系数趋近于1,粒子被完全反射,即粒子没有机会进入到右侧区域(Ⅱ).实际上,当能量E<0,粒子都将被完全反射,情况与2中的例子相同.
有的同学可能会对这一结果产生疑问.坐标的选择完全是人为的呀,为什么我们把坐标轴向上移动了V0而已,反射系数的表达式就有所不同了.粒子能量与势的关系均为V0=βE,其散射结果难道不应该是相同的吗?这里可能大家忽略了一个细节——考虑两种不同情况下粒子以相同能量E入射:从经典的观点考虑,当阶梯势高于零点,粒子的动能在x>0的区域为E-V0,而在x<0的区域为E;而当阶梯势与零点平齐,粒子的动能在x>0的区域为E,在x<0的区域为E-(-V0)=E+V0.也就是说以相同能量入射的粒子,在这两种势分布下,在x>0的区域其动能分别为E-V0和E,在x<0的区域,其动能分别为E和E+V0.所以,从能量零点选取的角度考虑,一种情况下入射能量为E对应另一种情况下入射能量为E-V0的情况.当入射粒子能量与阶梯势的相对关系一致时,所得的结果才会相同.
由一道简单的一维阶梯势的问题,我们竟然可以得到这么多有趣的结果.这也启发我们对很多《量子力学》中的问题需要举一反三.我们传统的课堂讲授内容可能更偏向于横向的比较,比如一维无限深势阱、一维有限深势阱、一维谐振子……而对问题的纵向延伸做得不够.这样做的结果是,同学们对老师课堂讲的例题能听懂,但是自己做习题就完全无从下手.此文中这样的举一反三既可以增加一点课程的趣味性,也能够激励学生思考,对学过的内容提出新的问题,这就是培养学生研究能力的一个有益模式.
IssueofOneDimensionalStaircasePotentialWorthyofInferingOtherThingsfromOneFact
Lu AijiangYang Qinyu
(Science College,Donghua University,Shanghai201620)
Abstract:Based on the quantum mechanics problem with one dimensional (1D) step-like potential, many an interesting results have been obtained.The moving directions of the injected particles and the position of the step-like potential are attributed to the main facets of this problem.It is a good exercise about 1D stationary state,and is a typical problem to show the specialty of quantum mechanics.
Keywords:step-like potential;potential function;transmission coefficient;reflectance
