基于改进BEMD的Gabor-2DPCA掌纹识别
2018-07-13张雪锋吕冰姿
张雪锋,吕冰姿
(西安邮电大学 通信与信息工程学院, 陕西 西安 710061)
生物特征识别技术已经成为当前身份识别领域的主要技术之一[1]。常用的生物特征有语音、指纹、掌纹、虹膜、人脸、DNA等[2]。其中,由于掌纹具有采集方便、纹理特征丰富、易于识别等特性,已经被应用于身份识别的众多领域[3]。
掌纹识别的关键技术是特征提取。目前,主要的掌纹特征提取技术包括:基于掌纹结构的特征提取,如点特征、线特征[4];基于掌纹纹理的特征提取,如灰度共生矩阵、Gabor变换[5-6];基于空域-频域分析的特征提取,如傅里叶变换、小波变换等[7-8];基于子空间的掌纹特征提取,如主成分分析(principal component analysis,PCA)、线性判别分析(linear discriminant analysis,LDA)、独立成分分析(independent component analysis,ICA)[3]
二维经验模式分解(bidemensional empirical mode decomposition,BEMD)是一种具有自适应性的时频局部化多尺度分析算法[9],被广泛应用于图像处理中,如图像压缩、图像去噪、图像轮廓提取[10-11]等。基于BEMD的掌纹处理算法将掌纹图像分解成从高频到低频、具有不同特征尺度的固有模态分量(intrinsic mode function,IMF)和一个残余分量。传统的BEMD算法存在着边界效应、曲面插值、筛分停止条件[12]等不足,后续学者对算法进行了改进,文献[13]提出了一种新的筛分停止条件,文献[14]针对分解过程中的边界效应提出了改进方案。文献[15]提出利用前4个IMF分量重构掌纹图像并用于掌纹识别。
主成分分析(principal component analysis,PCA)是一种线性降维的多元统计分析法,现已广泛应用于人脸、指纹、掌纹、虹膜的特征提取和识别中[16]。将二维的掌纹图像矩阵转化成一维的图像向量,然后进行PCA分析,计算量大,识别率不高。为此,提出了二维主成分分析(two dimensional principal component analysis,2DPCA)方法[17],将图像矩阵经过线性投影,构造行向量和列向量,变换为散度矩阵。2DPCA有效改进了PCA的相关性能,但鉴于掌纹图像具有较多的纹理特征,直接用2DPCA算法识别率不高[18]。
为了提高算法的精确率和掌纹的识别率,本文拟提出一种基于BEMD算法的掌纹识别改进算法。该算法首先用改进的BEMD算法分解图像,剔除残余低频分量,重构图像;然后经过Gabor变换将图像分解成多个纹理特征子图像,利用2DPCA算法提取特征,将样本分成训练集和测试集;最后通过计算样本欧氏距离识别掌纹图像。
1 算法流程及掌纹图像的预处理
1.1 算法流程
基于改进BEMD的Gabor-2DPCA掌纹识别算法,包括3个模块:掌纹预处理、特征提取、特征降维和识别,其流程如图1所示。
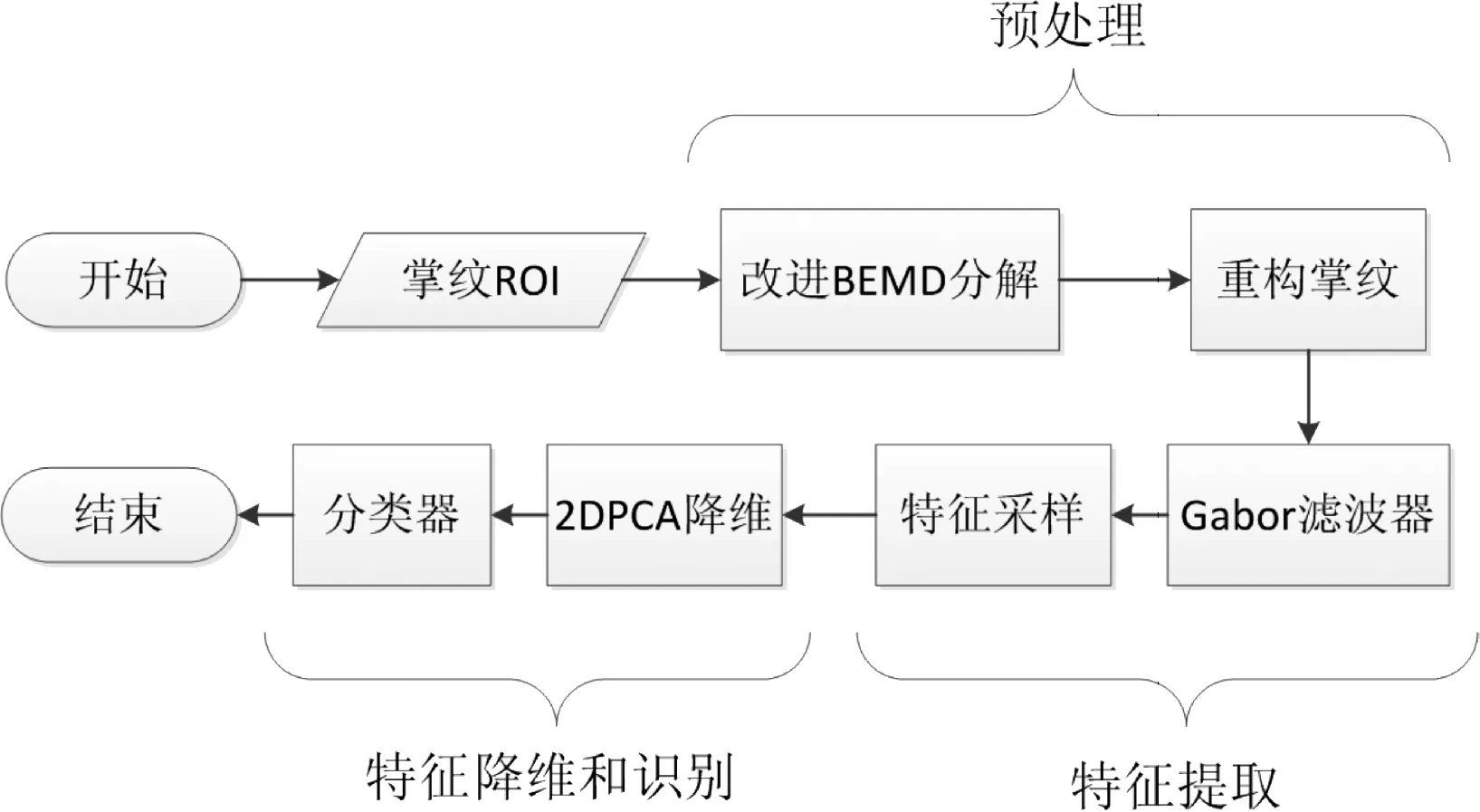
图1 掌纹识别系统结构框图
预处理阶段采用BEMD改进算法重构掌纹图像;特征提取阶段构造Gabor滤波器进行特征采样,提取掌纹的尺度和方向特征;特征降维和识别阶段采取2DPCA算法,将采样特征降维处理,并构造分类器进行掌纹识别。
1.2 掌纹图像的预处理
在掌纹识别系统中,预处理是一个很重要的过程,所提算法采用128×128的掌纹感兴趣区域(region of interesting,ROI),在原有BEMD算法的基础上提出了BEMD改进算法,剔除残余量,采用前4个IMF分量重构掌纹图像。
1.2.1BEMD算法
BEMD算法[9]利用形态学的方法找出图像的极值点,将这些极值点拟合成极值包络面,并做差求均值包络面,用原图像减去均值包络面得到IMF分量,由此分离出包含掌纹纹理信息的,不同频率和尺度的掌纹图像IMF分量。BEMD算法的具体实现过程如下。
步骤1初始化原图像,并将图像延拓,计算图像的局部极值。
步骤2将上、下极值拟合成极值包络面,采用Delaunay三角剖分和3次样条插值函数相结合的方法拟合极值包络面。
步骤3求均值包络面,并计算图像与均值包络面差值。
步骤4判断是否满足筛分终止条件。
步骤5重复前3个步骤,若满足给定的终止条件则停止循环,将图像分解成若干IMF分量和1个残余分量。
BEMD算法在拟合极值包络面,处理端点数据时,由于端点部分不一定是极值数据,也不满足插值条件。在循环插值和筛分的过程中,边界数据容易发生异变,使得分量图像边界失真,扩散到图像内部数据,甚至污染图像,随着筛分步骤的进行,边界效应的影响会越来越大。另外,现有的筛分停止准则容易引起图像过分解或欠分解[19]。针对以上2个方面的问题,提出一种改进的BEMD算法实现掌纹图像的预处理。
1.2.2改进的BEMD算法
输入图像r1,1(x,y)=f(x,y),x∈[0,M],y∈[0,N],M,N是原图像的行数和列数,将r1,1(x,y)作为输入图像,改进算法的具体实现步骤如下。
步骤1采用边界对称延拓方法预处理图像,选择100个延拓像素,将图像先上、下延拓100个像素,然后上、下、左、右各延拓100个像素。延拓后的图像边界数据也作为内部数据用于后续BEMD分解处理。
将原始图像经过第j次分解(j=1,2,…,J)后的第l(l=1,2,…,L)个IMF分量表示为rl,j(x,y)。
步骤2采用八邻域法计算rl,j(x,y)的局部极大值和局部极小值,并将其拟合得到极大值、极小值包络曲面cmaxlj(x,y)和cminlj(x,y)。
步骤3求均值包络面
(1)
步骤4计算图像与均值包络面的差值
hl,j(x,y)=rl,j(x,y)-ml,j(x,y)。
(2)
步骤5计算并判断筛分终止条件
(3)
若满足条件SD≤β,则hl,j(x,y)为第j个IMF分量,记为IMFj;若不满足条件,则令
rl,j+1(x,y)=hl,j(x,y)。
传统算法容易产生过分解和欠分解,若β太小,则计算时间长,若β太大,则分量结果不准确。实际应用中一般β的取值范围在0.2~0.3之间,β的取值越小,分解越准确;取值越大,用时越短。为了提高准确性,本文选取0.2作为筛分停止阈值。
计算相邻二次筛分方差的差值Δj,设定阈值θ,如果差值绝对值小于等于阈值,则筛分停止,否则继续筛分。本文只取前4个IMF分量,为了避免过分解和欠分解,差分阈值θ设定为0.05[14]。
Δj=SDj-SDj-1, |Δj|≤θ。
(4)
继续步骤2至4,直到满足上述停止条件为止,记Hl(x,y)=hl,j(x,y)。
步骤6计算残余分量
rl+1,j(x,y)=hl,j(x,y)-Hl(x,y)。
(5)
若残余分量中至少包含2个极值点,则将残余分量rl+1,j(x,y)作为待分解图像重复分解,直到残余分量rL(x,y)中没有极值点,则分解结束。最后得到分解结果
(6)
本文选取L=4,按照以上步骤就可以将一幅掌纹图像分解为频率从高到低的4幅2维固有模态分量和1个残余分量,去除残余分量,用4个IMF分量重构图像,重构方法如下。
(7)
通过式(7)能够有效重构出原图像的信息。
2 二维Gabor变换提取图像特征
去除信号在空间或时间尺度的关联关系,提取出图像的频率、方向、纹理特征等局部特征,是在时频域进行信号分析处理的重要工具。二维Gabor变换常用于图像的分解,其可以进行多分辨率分析,在时域和频域都有表征信号局部特征的能力,在生物识别领域中往往结合基于子空间的方法应用于人脸、掌纹、虹膜、指纹识别。
二维Gabor小波滤波器用一组滤波器函数与给定图像信号卷积来表示或逼近一个信号,其函数形式通常表示如下。
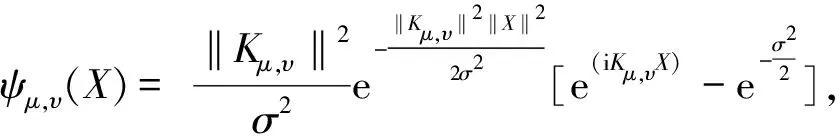
(8)
将掌纹ROI图像与滤波器核函数卷积得到纹理特征子图像,方法如下。
Iμ,υ(X)=Iroi(X)*ψμ,υ(X)。
(9)
将掌纹图像先进行高斯滤波预处理增强,使其纹理特征更加明显。然后采用5方向,4尺度构造的20个滤波器对重构的掌纹图像进行小波变换,将输入图像与Gabor核函数进行卷积,但分解的图像由于维数过大,直接进行识别计算量大,并对所得到的结果进行下采样,采样因子为8,将掌纹图像分辨率降为16×16,输出为256×20的特征向量。
3 基于2DPCA的特征降维与图像识别
提取了掌纹图像特征后,需要对其降维、训练和识别。
3.1 图像特征降维
利用PCA算法降维,可以减少原始样本里大量数据之间的相关性,提取出一定累计贡献率占比的互不相关的低维综合变量,新的综合变量是原来变量的线性组合。提取出的第一个综合变量称为F1,第二个为F2,以此类推,直到提取出的综合变量线性总和满足总体数据的累计贡献率即可,一般要求累计贡献率达到85%以上[20]。
2DPCA是在PCA算法基础上的改进,直接利用掌纹图像二维投影形成二维矩阵,在特征提取中解决了传统PCA算法将二维矩阵转化为一维向量时产生的小样本问题。其特征空间图像形成的协方差矩阵数据量更小,处理速度更快,准确性更高。给定训练样本图像集{I1,I2,…,IN},基于2DPCA算法的生物特征识别过程的基本步骤如下。
步骤1计算训练样本协方差矩阵、特征值、特征向量。
步骤2计算训练集中的平均图像矩阵
(10)
步骤3计算每个训练图像的协方差矩阵
(11)
步骤4计算每个协方差矩阵的特征值及其对应的特征向量。n维变换后的数据维数向量
WJ={W1,W2,…,Wj},
特征空间转化关系为
Y=IjWJ。
3.2 图像的训练和识别
(1) 训练阶段
输入训练掌纹图像,用2DPCA算法提取特征向量矩阵并计算其在特征空间的投影。计算训练集中的图像平均特征、协方差矩阵及其特征值和特征向量,其投影构成“特征掌”空间。求得特征值λi。贡献率
(12)
本文取贡献率为99%,φ≥99%即训练样本在前p个特征向量上的投影有99%的能量。
(2) 识别阶段
计算测试样本在特征空间的投影,计算测试样本点与所有的训练样本点之间的距离,求出最小距离。同时计算测试样本点与该同一样本的训练样本点之间的距离,求出最小距离。比较两个距离是否相等,若相等则识别成功;若不相等,则识别错误并输出错误样本。
训练和识别流程,如图2所示。

图2 训练和识别流程图
4 实验结果及分析
采取香港理工大学的PolyU掌纹数据库中的100种掌纹,每种掌纹有6个掌纹样本,共600张图像。设备采用i5-3210M的CPU,主频2.5 GHz,内存4 GB的工作平台,应用MATLAB2010b软件编写程序仿真实验。
首先对掌纹图像按照文献[21]的方法进行预处理,将原图像去噪、二值化、提取轮廓、建坐标系、定位分割获得掌纹感兴趣(ROI)区域,并将图像分辨率统一为128×128。其次对每个掌纹分别用BEMD算法和改进的BEMD算法分解,提取前4个IMF分量重构掌纹,剔除光照、背景等因素对掌纹图像的影响,统计掌纹图像并用高斯滤波器增强预处理图像,突出高频部分并使细节更清晰。然后对每个掌纹用2DGabor滤波器分解,得到5个尺度、4个方向的20个输出图像,并对所得到的结果进行下采样,将掌纹图像分辨率降为16×16,输出为256×20的特征向量,既突出了图像的不同方向尺度和频率特征,也减少了处理数据量。最后用2DPCA算法分别对经过2DGabor处理过的原始掌纹、BEMD算法重构掌纹和改进的BEMD算法重构掌纹进行特征提取,并计算3种不同方式下各样本图片特征之间的欧氏距离对掌纹进行分类识别。
4.1 掌纹纹理特征提取
示例掌纹ROI,如图3所示。

图3 示例掌纹ROI图
分别使用BEMD算法和改进的BEMD算法分解掌纹图像的实验结果,如图4-5所示。

图4BEMD算法分解掌纹结果

图5 改进BEMD算法分解掌纹结果
仿真结果表明,BEMD分解在IMF3分量时出现边界效应,在IMF4中边界效应更明显,对图像有明显的污染,丢失部分掌纹图像信息。改进的BEMD分解则有效抑制了边界效应,分解的前四个分量均无边界效应。改进后的BEMD算法较原有算法提取的4个分量包含了更多的图像高频信息,更好地去除了掌纹中受到背景影响的低频信息。
剔除图4和图5的残余分量,用前4个分量重构掌纹图像。BEMD算法改进前后的掌纹重构结果,如图6-7所示。

图6 用前4个分量重构掌纹图像结果
由图6可以看出,由于边界效应的图像污染,传统BEMD算法重构的掌纹图丢失了部分掌纹信息,改进的BEMD掌纹图完整的保留了剔除低频分量后的掌纹信息。而且,改进算法重构的掌纹图较传统算法纹理更清晰,背景影响更小。
采用灰度共生矩阵中的能量、熵、对比度、相关性4个指标[22]来对比算法改进前后重构的掌纹图以及原图的纹理特征。能量即角二阶矩,反映了图像灰度分布均匀程度和纹理粗细度,能量值越小纹理越细。熵用来度量图像纹理信息量,表示纹理复杂程度,熵值越大,图像含有纹理信息越多。对比度反映图像像素及其亮度对比情况,对比度越大,图像越清晰,纹理线越明显。相关性表示矩阵中元素不同方向的相似度,其值越小则矩阵中相关元素相差越大,越利于识别[23]。
任意抽取7个掌纹样本,取灰度共生矩阵4个方向(0°、45°、90°、135°)的特征值的平均值作为图像纹理特征,计算每个掌纹样本中6幅图像的各个纹理特征参数的平均值,如表1所示。
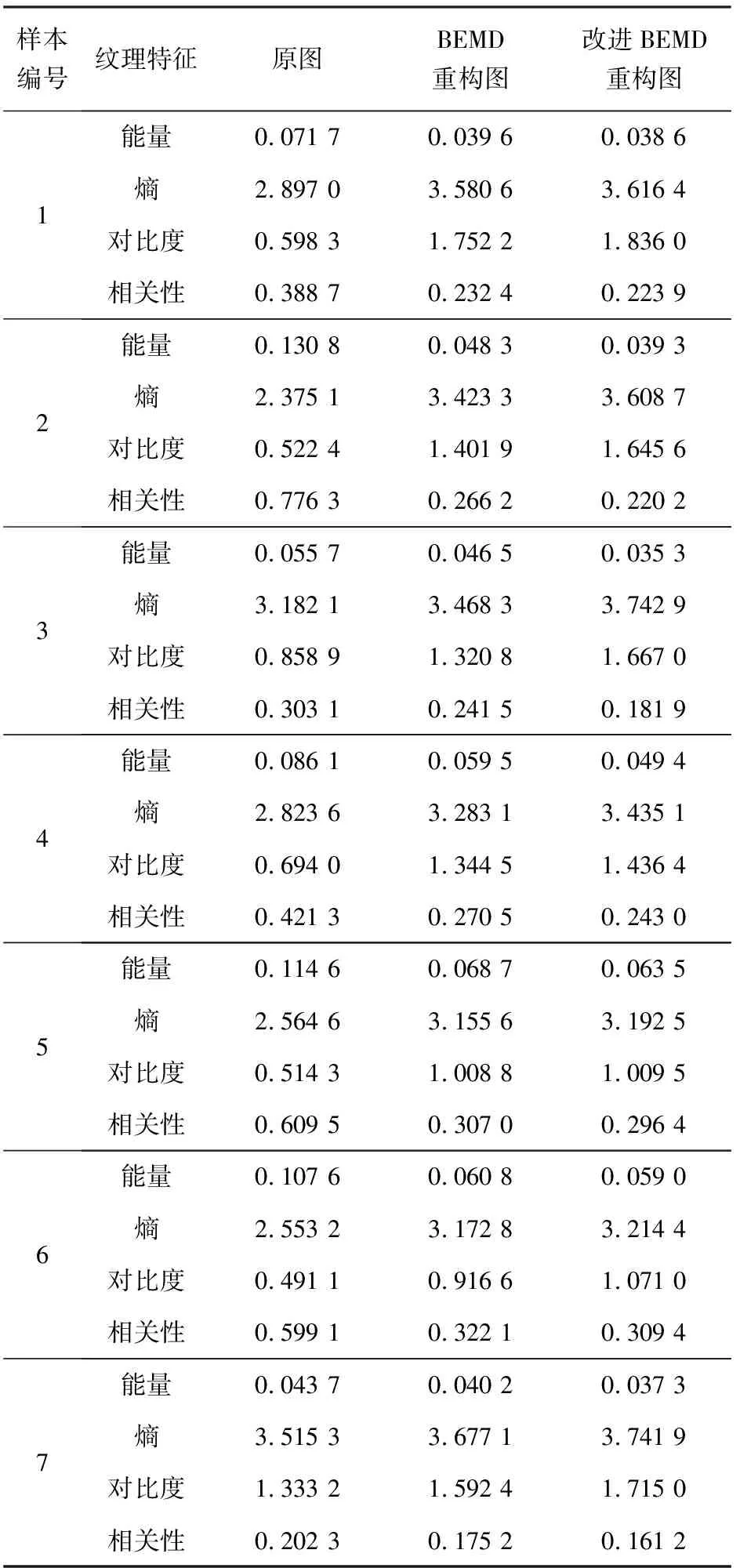
表1 不同方法掌纹图的纹理特征
对比原图,BEMD重构图和改进算法重构图,可以看出,重构掌纹图较原图更清晰,包含更多的纹理特征,更细的纹理。改进算法重构的掌纹图较原算法有更大的优越性。为了验证其识别性能,本文进行了进一步的仿真实验。
4.2 识别结果对照
采用取每个样本6幅掌纹图中的前3幅图片作为训练图像,每个样本中的后3幅图片作为识别图像。用3种算法测试识别性能。
4.2.1不同特征向量维数的识别率
(1) 文献[24]算法,采用原图直接进行二维Gabor分解,并通过2DPCA算法识别。
(2) 本文算法一,采用BEMD算法重构的掌纹图进行二维Gabor分解,并通过2DPCA算法识别。
(3) 本文算法二,采用改进的BEMD算法重构的掌纹图像进行二维Gabor分解,并通过2DPCA算法识别。
采用2DGabor分解示例掌纹,将其分解为5尺度,4方向的20幅特征子图,然后采用2DPCA算法对掌纹子图像降维处理,并进行特征提取,测试不同特征向量维数(20、40、60、80、100、120)的各个方案的掌纹识别率,实验结果如表2所示。

表2 不同特征向量维数的识别率
由表2实验结果可知,随着特征向量维数的递增,掌纹识别率逐步提高。当特征向量维数超过80时,本文算法一和本文算法二的识别率均高于文献[24]算法。算法二的识别率较算法一也有提升,说明BEMD算法重构的掌纹图像较原图像有更高的识别率,而改进的BEMD算法重构的掌纹图像有更优越的识别性能。在特征向量维数为100的时候,改进算法重构的掌纹图有99.3%的识别率。
4.2.2小样本实验
为了验证算法的性能和应用价值,进一步进行了的交叉和对照验证实验。由以上实验结果可知,当特征向量维数为100时,算法的识别性能最好,后续的验证实验在特征向量维数为100时进行。
将掌纹库每个样本的六张图编号为1~6,分别测试每个样本编号掌纹图像的识别率,每个相同样本编号的100张图像组成训练集,剩余500张图片组成测试集,分别对每个样本做实验,并计算每个编号样本的平均识别率记录,实验结果如表3所示。

表3 单一样本下3种算法的识别率
由表3可知,文献[24]算法、本文算法一和本文算法二的评价识别率分别为95.3%、95.6%和97.0%。结合传统BEMD的算法一较原文献[24]算法识别率有小幅提升,改进BEMD算法应用之后的算法二则有更多的提升。实验结果表明,将改进的BEMD算法应用于掌纹识别系统中可提高系统的识别率,在掌纹识别中的单一样本下的实验具有适用性。
此外,为了更好的测试改进BEMD算法在2DGabor+2DPCA掌纹识别系统中小样本问题的解决效果,随机选取掌纹库的100个样本中的1幅、2幅、3幅图作为训练样本,分别形成100、200、300幅掌纹图的不同训练集,对应剩余的500、400、300幅图作为测试样本集。实验重复选取5次不同样本组合进行实验,取5次结果的平均值作为识别结果,实验结果如表4所示。
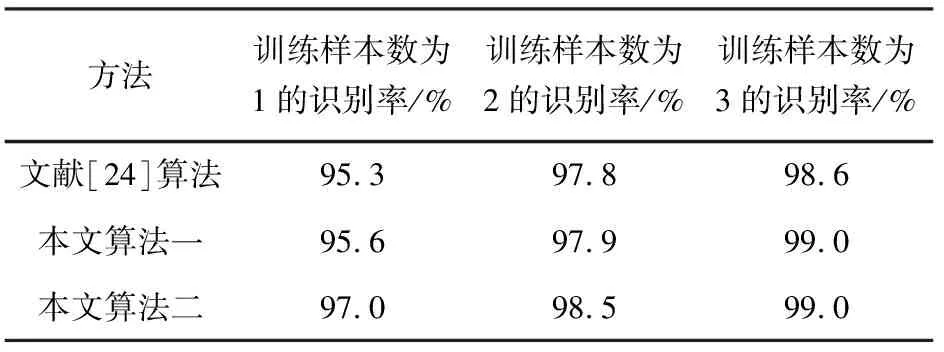
表4 不同训练样本下不同算法的平均识别率
由表4可以看出,随着训练样本数的增加,识别率逐步上升,本文算法一、二较文献[24]算法的识别率均有提升,因此,将BEMD重构的掌纹图应用于掌纹识别可以解决2DPCA识别系统中的小样本问题,改进的BEMD算法重构掌纹图较传统算法有更好的识别性能,训练样本数为3时,系统识别率达到99.0%。
4.2.3算法识别性能分析
特征向量通过计算类内类间各点之间的欧氏距离分类,是一种二元分类法,在类间距离不平衡的情况下,通常用ROC曲线评价分类器性能。ROC曲线的横坐标为错误接受率,纵坐标为正确接受率,用曲线下包围的面积来衡量分类器的可信度,ROC曲线包围的面积越大算法性能越好[25]。特征向量维数取100,3种算法的ROC曲线如图7所示。
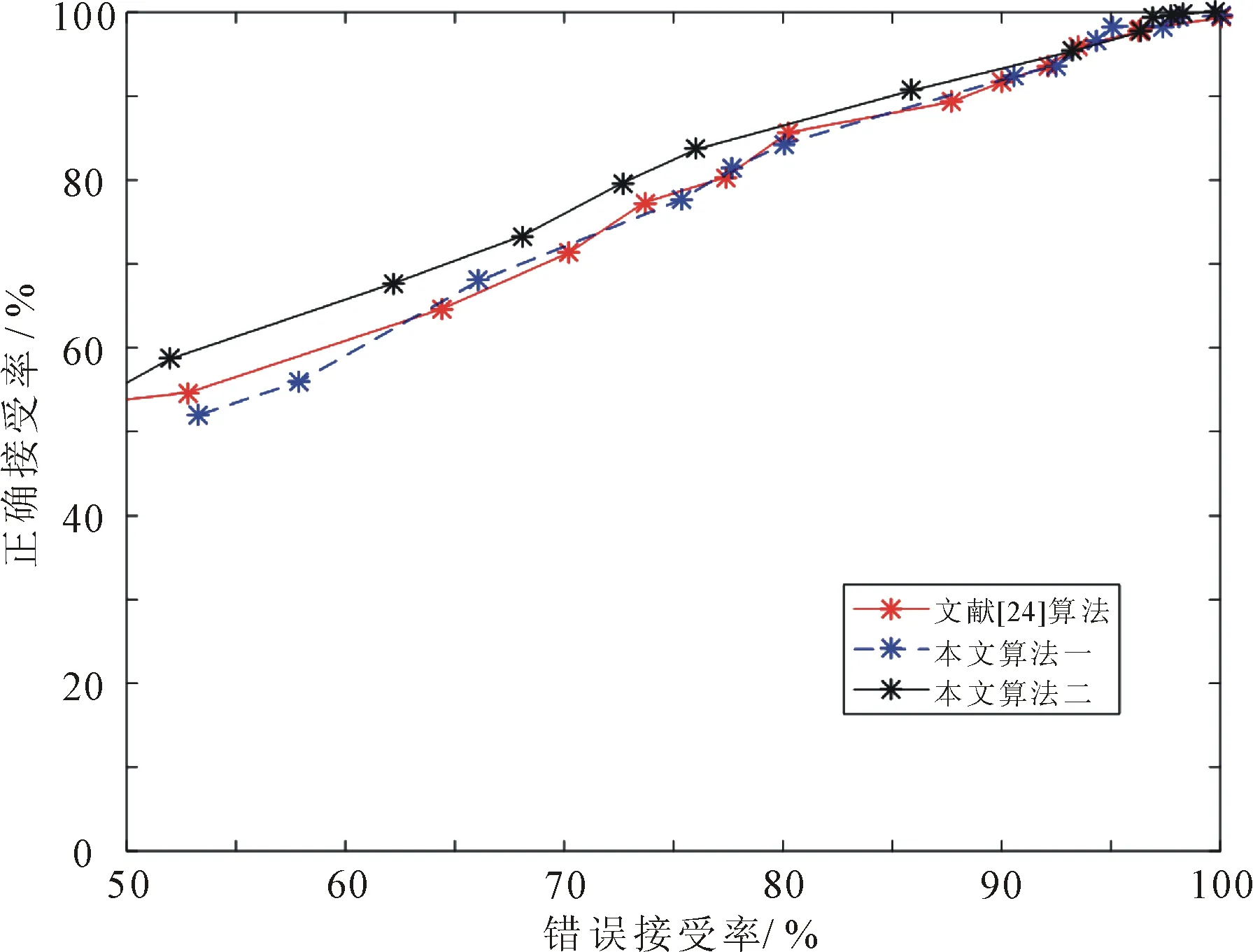
图7 三种算法的ROC曲线
由图7可以看出,本文的算法二较文献[24]算法和算法一的ROC曲线更靠近横坐标轴,包围的面积更大,有更好的识别性能和更高的可信度。
5 结论
在BEMD算法的基础上,针对图像延拓产生的边界效应和分解过程中的过分解和欠分解问题,提出了一种改进算法,将传统的镜像延拓替换成了对称延拓,其次,在原有筛分停止准则的基础上,增加了差值阈值,最后,剔除残余分量,重构掌纹图像,并进一步分析了重构掌纹的纹理特征。结合二维Gabor分解和2DPCA算法在PolyU掌纹库上测试了改进BEMD算法重构掌纹的识别性能。
实验结果表明,改进算法重构掌纹图较原图更清晰,包含更多的纹理特征,更细的纹理。有更优越的识别性能,不同的样本集测试下识别率较原有算法均有提升,最高可达99.33%,与此同时,该算法ROC曲线包裹面积更大,有更好的识别性能。
