基于GM(1,1)试卷难度系数修正模型的学生成绩预测
2018-07-13吴楠胡尧李小林王丹胡娟李玉凯舒丹陈青凤
吴楠 胡尧 李小林 王丹 胡娟 李玉凯 舒丹 陈青凤

摘 要:学生成绩是教学评估的一项重要衡量指标,考虑学生考试成绩特点提出了一种基于试卷难度系数变化的GM(1,1)修正模型,并运用此模型对花溪一中考试成绩进行预测,实践证明该修正模型能减少误差,提升预测精度。
关键词:成绩预测; 发展灰数;后验差检验; 小误差概率;难度系数
中图分类号:O212
文献标识码: A
随着科技数据信息的发展,探索新的教学方法、前瞻性数据化建设校园是校方义不容辞的责任。合理运用信息技术能有效地解决教学中许多问题。目前中小学对数据的应用多限于成绩查询和一些常规统计,如平均分、及格率、最高分等。这些描述性统计分析只是某一次考试当前情况的体现,无法挖掘数据中存在的关系和规则,无法根据现有的各项数据预测学生成绩以及学生今后发展趋势。本文通过与中学老师的沟通,了解中学考试成绩展现特性,结合当前考试形式,对学生成绩进行整理分析,通过搭建数学模型,实现对学生最终中考成绩进行预测分析,并选取贵州省贵阳市花溪区第一中学(简称花溪一中)考试成绩进行分析,验证模型有效性。
1 数据预处理
数据来源于花溪一中2017届学生初中各次考试成绩(以下简称学生成绩)。考虑中考科目为:数学、语文、英语、理综(物理、化学),故选取花溪一中2017届学生8年级至9年级数学、语文、英语、物理、化学成绩进行整理,统计共634名学生的成绩。为方便数据读取和分析,引入一些符号标记对原始各次考试进行重新标记,例如:“数学分数81”表示“八年级上学期期末考试成绩”,“数学分数911”表示“九年级上学期第一次月考数学成绩”,其他类似。表1展现了整理后的数学成绩的部分数据。
1.1 缺失值情况分析
数据缺失值分布情况与分析结果息息相关,图1是数学考试成绩的缺失数据情况。图中,浅色为缺失值,深色为完整数据,图(a)体现各次考试的缺失数据量,图(b)展示缺失数据在整个数据中的位置。数学成绩总数据为634×16的数据框,其中616名的成绩数据完整有效,仅18名同学的数学成绩有缺失。缺失值共21个,占总数据量10144的0.21%,缺失率小于10%,指标的信息完整度均在理论范围内[1]。
同样的方法,可得出各科成绩数据缺失情况如表2所示,数据缺失比率均小于10%,故不会影响分析结果。
1.2 缺失值补齐
结合花溪一中实际考试成绩情况,对学生考试成绩进行填补,同一考生缺失数据较多的予以剔除,最终建立634名考生成绩总表。为便于后期建模分析,选取学生八年级上下学期期末考试成绩、九年级全部数据及花溪区区考成绩和贵阳市适应性考试作为最终分析的数据,并对缺失部分予以补齐。常用的缺失值补齐方法有均值补齐法、中位数补齐法、众数补齐法等,结合学生成绩实际情况,采取均值补齐法。
2 灰色预测模型概述
2.1 灰色预测模型
灰色预测对既含有已知信息又含有不确定信息的系统进行预则,即对在一定范围内变化的、与时间有关的灰色过程进行预测。灰色预测通过鉴别系统因素之间发展趋势的相异程度,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况[2]。
在充分使用数据的基础上,建立GM(1,1)模型,分别对考生各科成绩进行预测。
2.2 灰色预测GM(1,1)模型
3.2 基于GM(1,1) 试卷难度系数修正模型的实现
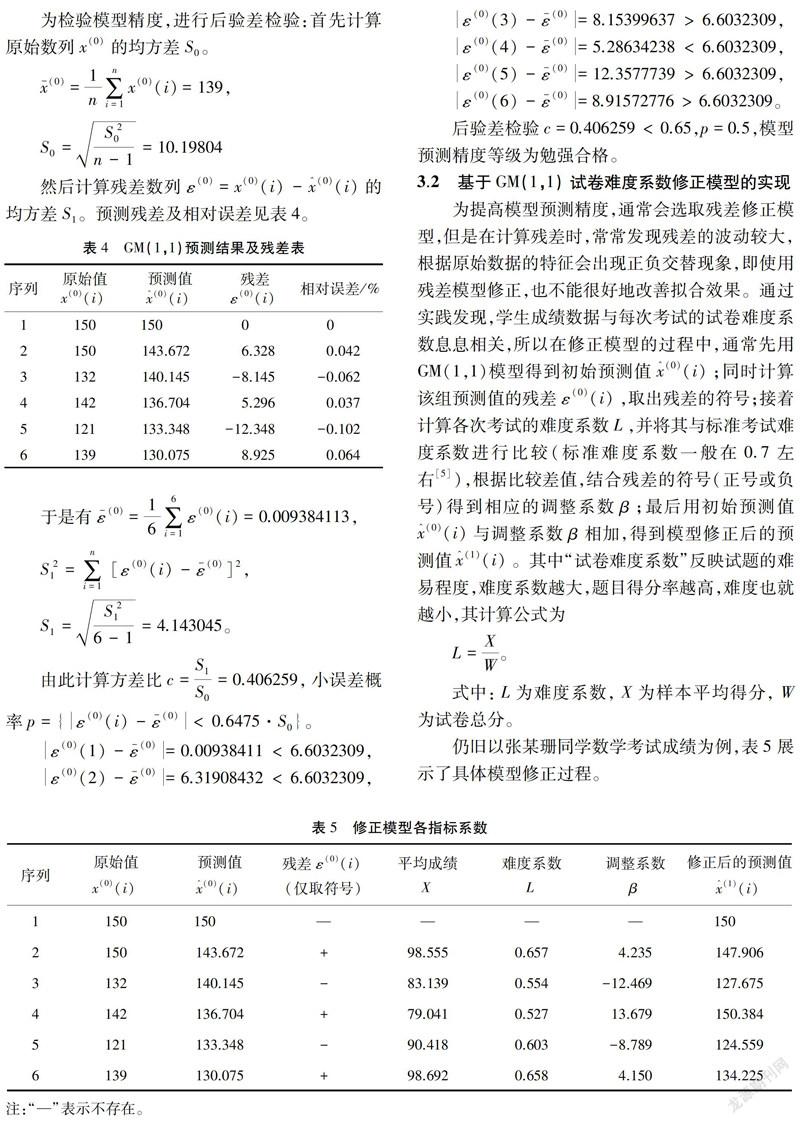
为提高模型预测精度,通常会选取残差修正模型,但是在计算残差时,常常发现残差的波动较大,根据原始数据的特征会出现正负交替现象,即使用残差模型修正,也不能很好地改善拟合效果。通过实践发现,学生成绩数据与每次考试的试卷难度系数息息相关,所以在修正模型的过程中,
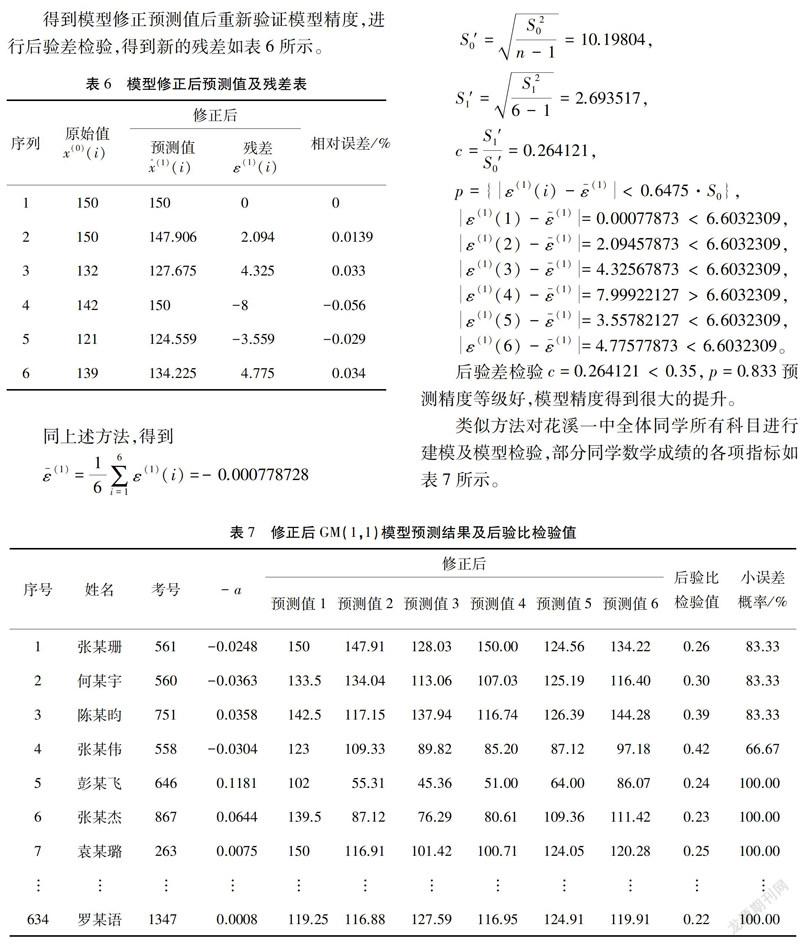
得到模型修正预测值后重新验证模型精度,进行后验差检验,得到新的残差如表6所示。
类似方法对花溪一中全体同学所有科目进行建模及模型检验,部分同学数学成绩的各项指标如表7所示。
经计算,所有数据的发展系数a均小于1,故均可使用GM(1,1)进行建模预测,通过残差符号结合难度系数得到各模型调整系数对模型进行修正,最终得到修正后的模型预测值,并进行新的后验比检验,结果除极少部分同学考试成绩波动特别大导致模型预测效果欠佳,其余均显示模型预测通过后验比检验和小误差概率检验,效果良好。
3.3 花溪一中学生中考成绩预测
综上可以用修正后的GM(1,1)模型分别对花溪一中学生中考单科和总分成绩(预测总分加上50分体育成绩所得)进行预测。首先对总分进行预测。据了解,贵阳市今年中考难度系数在0.75,以该难度系数为标准,对学生中考成绩预测,预测结果如表8所示(仅选取前50名展示)。
由预测结果统计:600以上约为30人。据最终花溪一中公布的2017年中考考试成绩(由于资源有限,仅获取了600以上同学总成绩和1班同学的各科目成绩),600以上为35人(含加分政策),根据修正后GM(1,1)模型预测出来的30人均包含在内。利用修正后GM(1,1)模型预测的花溪一中学生中考成绩分布如图2所示。
其次,对花溪一中学生中考单科成绩进行预测,表9展示部分同学各科成绩预测结果。
为验证预测结果的准确率,利用获得的1班同学的总分及单科成绩数据对预测結果进行误差分析,经计算总成绩预测的均方误差为:-4.866;语文、数学、英语、物理、化学的均方误差分别为:0.197、0.545、0.258、2.924,平均误差均不超过5分,说明模型预测效果良好。
4 结论
从学生成绩残差特性出发,提出一种基于试卷难度系数变化的GM(1,1)修正模型,这符合“灰色系统理论的研究对象信息不完全,准则具有多重性,模型非惟一性”的特点。且经实践表明,修正后的模型能提升学生成绩预测模型精度。在预测学生成绩时,可以推广使用。
参考文献:
[1]COHEN J,COHEN P,WEST S G, et al.Applied multiple regression/correlation analysis for the behavioral sciences[J].Journal of the Royal Statistical Society, 2003,52(4):691.
[2]杨华龙,刘金霞,郑斌.灰色预测GM(1,1)模型的改进及应用[J].数学的实践与认识,2011,41(23):39-46.
[3]李梦婉,沙秀艳.基于GM(1,1)灰色预测模型的改进与应用[J].计算机工程与应用,2016,52(4):24-30.
[4]罗党, 刘思峰, 党耀国. 灰色模型GM(1,1)优化[J].中国工程科学,2003,5(8):50-53.
[5]何瑞林. 中考试卷难度系数7:2:1[N].扬州日报,2008-06-13(A03).
(责任编辑:周晓南)
