计及信号随机延时的电力系统小干扰概率稳定性分析

陈　中, 唐浩然, 袁宇波, 周　涛, 李虎成, 许　扬

(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 江苏省智能电网技术与装备重点实验室, 江苏省南京市 210096; 3. 国网江苏省电力有限公司, 江苏省南京市 211103)

0　引言

随着计算机网络通信技术的不断发展,广域测量系统(wide area measurement system,WAMS)为分析区域间低频振荡及其抑制提供了新的手段[1-2]。在广域附加阻尼控制器的应用中延时的存在是不可避免的问题,延时是控制律失效、运行状况恶化和系统失稳的一种重要诱因[3]。广域测量系统由多种通信媒质组成,结构复杂,传输装置、传输媒介的不同,使得传输通道的通信延时具有不确定性[4]。

近年来,对固定延时下的系统稳定性研究与控制器设计已有较多的研究[5],广泛应用的方法有Smith预测方法[6]以及Pade近似方法[7]。但是受网络环境变化的影响,WAMS网络中的通信延时往往是随机的。文献[8]通过对江苏WAMS的实测指出,传输过程中可变延时的大小受数据量变化的影响,并且延时范围的概率满足近似正态分布。文献[9-11]采用不同的预测算法对具有延时特性的广域信号进行补偿,从而使得在一定通信延时范围内,广域控制器能够获得近似于实时的信号数据。以上方法均是从信号预测补偿的角度出发减少随机延时对系统稳定性的影响。文献[12-14]从模型出发,通过不同方法构造新型Lyapunov-Krasovskii泛函建立了时变时滞电力系统模型,并通过线性矩阵不等式(linear matrix inequalities,LMI)实现了系统最大允许时滞的求解与广域阻尼控制器设计,如何减少判据保守性是研究难点。文献[15]通过数学期望建模方法模拟了通信网络随机延时对广域控制性能的影响,未进一步给出系统稳定性分析方法。目前,在电力系统领域考虑随机延时对系统稳定性的影响的研究工作尚处于发展阶段,因此需要深入研究WAMS系统中广域信号的随机延时特性对于电力系统小干扰稳定性的影响机制。

电力系统概率稳定性分析最早由Burchett和Heydt于1978年提出[16]。现有研究主要考虑电力系统网络拓扑与节点注入功率的不确定性[17],较少考虑通信系统的随机性对电力系统稳定性的影响。由于通信延时的不确定性,采用广域测量信号的电力系统特征根将以一定的概率分布在某些区间内。根据延时系统临界特征根的概率分布,就能近似得到整个系统小干扰稳定的概率。

为研究广域信号在通信系统传输过程中,延时的随机分布特性对系统小干扰稳定的影响,本文采用半不变量与Gram-Charlier级数相结合的方法对具有随机延时的广域电力系统进行建模,并对不同延时分布参数下的电力系统小干扰概率稳定性进行了分析。进而提出了一种基于置信区间的计及广域信号随机分布延时的电力系统稳定器(PSS)参数鲁棒性设计方法。

1　计及延时的小干扰概率稳定计算模型

1.1　半不变量和Gram-Charlier级数

文献[18]对贵州电网广域控制系统中的信号延时进行分析后得出,可采用正态分布估计模型对实际广域系统中的信号延时进行拟合,故本文采用正态分布建立信号延时的估计模型(为不失一般性,也可隶属于其他任意分布形式)。信号延时的概率密度函数(probabilistic density function,PDF)为:

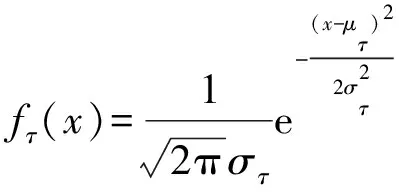
(1)

式中:μτ和στ分别为信号延时的均值和标准差。

针对式(1)所描述的信号延时,可通过Gram-Charlier级数展开的方法,获得广域控制系统临界特征根的概率密度函数,进而得出系统的小干扰概率稳定性,具体步骤如下。

1)计算随机变量的阶距与半不变量

随机变量延时可表示为τ=τ0+Δτ,其中τ0为随机变量的期望值,Δτ为随机扰动,其期望的表达式为:

E(Δτ)=E(τ-τ0)=E(τ)-E(τ0)=0

(2)

Δτ的一阶原点矩(期望值)为零,从而得出:

E(Δτ-E(Δτ))k=E(Δτ)k=E(τ-τ0)k=

E(τ-E(τ))k

(3)

式(3)表明Δτ的各阶原点矩都等于其中心距,而且等于τ的中心距。因而只要求出τ的各阶中心距,就是Δτ的各阶中心距。

半不变量γk是通过对随机变量的特征函数取对数而得到的[19],可得到:

(4)

式中:αk和βk分别为随机变量x的k阶原点矩和k阶中心距,其中k=1,2,…。

假设系统的特征根为λ=ξ±jω,则可得到式(5)所示的线性关系:

(5)

由概率论可知,随机变量a倍的k阶半不变量等于该变量的k阶半不变量的ak倍。因此，根据式(5)可得出特征根实部随机变化量Δξ的第k阶半不变量:

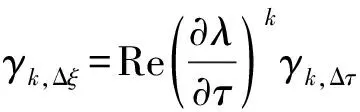
(6)

Δξ的第k阶中心距βk,Δξ可由其半不变量求得:

(7)

2)按Gram-Charlier级数展开确定特征根实部的概率密度函数

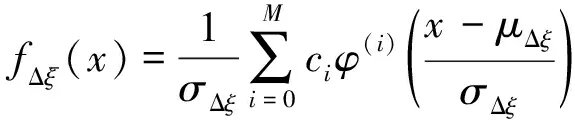
(8)

其中系数ci表示如下:

(9)

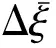
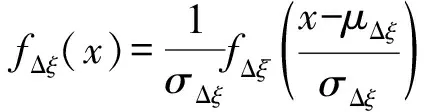
(10)

由于Δξ=ξ-ξ0,因此ξ的概率密度为:

fξ(x)=fΔξ(x-ξ0)

(11)

最后,可得到计及随机通信延时的电力系统小干扰稳定概率为:

(12)

1.2　基于阻尼转矩分析法的延时灵敏度计算

计算出式(6)中的参数∂λ/∂τ,即特征根对延时的灵敏度,是获得fξ(x)的难点与关键。本文将利用阻尼分析法与Pade近似相结合的方法计算出该灵敏度参数。

输入信号中含有延时的广域阻尼控制器线性化方程为:

Δu=G(s)Δyτ

(13)

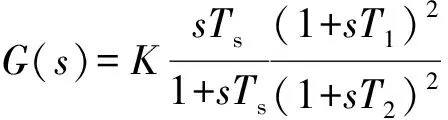
(14)

式中:Δyτ为含有延时的广域阻尼控制器的输入信号;G(s)为PSS的传递函数；K为放大环节的放大倍数；Ts为复位环节系数；T1和T2为相位补偿环节系数;Δu为输出信号。

设PSS输入信号Δyτ由L个广域信号组成,则Δyτ可表示为:

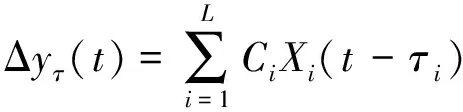
(15)

式中:Xi为系统具体的第i个广域信号;Ci为广域信号的权重;τi为第i个广域信号的延时。

对于同一控制器不同输入信号Xi,经过WAMS所需要的传输时间各不相同,即延时各不一样,但早到的信号需要等待同一时标的所有信号到达,故可认为Δyτ的延时由最后到达的广域信号的延时τmax决定,可表示为:

τmax=max(τi)i=1,2,…,L

(16)

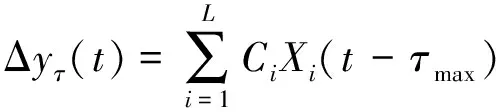
(17)

将式(17)从时域变换到频域可得:

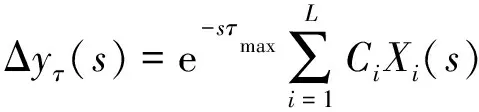
(18)

因此,可将输出信号Δu表示为:

(19)

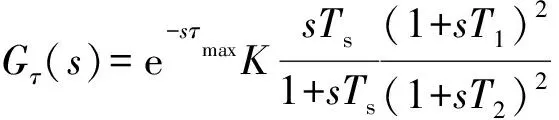
(20)

式中:Gτ(s)为计及延时的控制器传递函数,表明可将延时环节移动到控制器传递函数中;Δy为不含延时的控制器输入信号。

由式(19)和式(20)可知,此时控制器传递函数改变,但输入信号中已不包含延时信息,故可采用标准的阻尼转矩分析法(damping torque analysis,DTA)计算得到系统的阻尼转矩系数,进一步得到特征根相对于延时的灵敏度指标,具体推导过程如下。

阻尼转矩分析法指标的定义和计算公式为[20]:

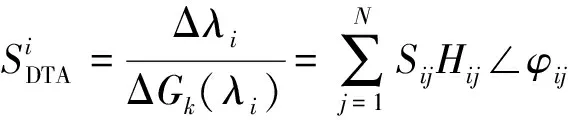
(21)

式中:λi为加入广域PSS后的第i个系统特征根;Δλi为第i个特征根的变化量;ΔGk(λi)为第k台PSS的传递函数的变化量;Sij为第i个特征根对第j号发电机的机电振荡回路提供的阻尼转矩的灵敏度;Hij∠φij为广域PSS对第j号发电机的机电振荡提供的阻尼转矩。

由式(20)和式(21)可得到:

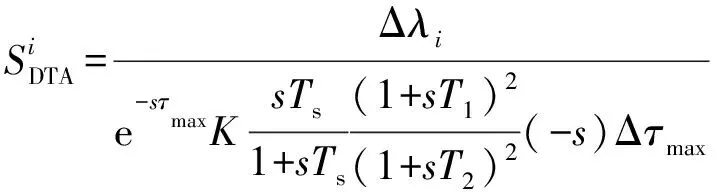
(22)

进一步,可以得到第i个特征根λi关于延时τmax的灵敏度:

(23)

由式(23)可知,由于延时环节e-sτmax的存在,系统的特征方程变为一个含有超越项的方程。本文采用Pade近似的方法将延时环节变化成一个高阶多项式,从而将具有超越项的延时微分方程变为普通的微分—代数方程。文献[21]指出采用2阶Pade近似即可有较高的准确性以及较快的计算速度,故本文对延时环节采用2阶Pade近似模型,式(23)变换为:

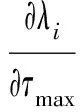
(24)

由式(6)、式(8)、式(10)、式(11)、式(12)以及式(24)共同组成了计及延时随机特性的电力系统小干扰稳定计算模型。

2　计及随机延时的PSS鲁棒性设计

不同延时模型下,系统特征根实部具有不同的统计特性。概率特征根的统计特性可用相应的均值、方差描述,并可由Gram-Charlier级数展开计算确定。

考虑到PSS参数的限制,可定义参数优化问题为:

(25)

T表示控制器中超前校正环节的时间常数T1至T4。PSS的增益环节设计与励磁系统相同,故仅需对补偿角度进行参数设计,使得PSS能够向系统提供最大的阻尼。对本文采用基于模拟退火的粒子群优化 (simulated annealing particle swarm optimization,SAPSO)算法对PSS控制器参数进行优化,模拟退火算法在搜索过程中具有概率突跳的能力,可在粒子搜索过程中克服标准粒子群算法容易陷入局部最优这一缺点。

3　算例分析

3.1　计及随机延时的小干扰概率稳定计算方法验证

两区四机系统是由两个区域经长距离输电线路相互连接构成的一个弱互联系统[22]。其中含有WAMS的系统模型图见附录A图A1,系统详细参数见附录A表A1至表A6。该系统的振荡模式中既包含了区域间振荡模式,也存在局部振荡模式。

以PSS安装在G1,相量测量单元(phasor measurement unit,PMU)安装在G1和G3,PMU将发电机转子信号传输到相量数据集中器(phasor data concentrator,PDC)后,取反馈信号Δω1-Δω3传输到广域PSS用以抑制系统区域间振荡。取控制器参数K=10,T2=T4=0.05,T1=T3=0.2。由于信号延时估计模型的参数可通过实测获得,本文以τ～N(0.1,0.052)为例,其中N(0.1,0.052)表示均值为0.1、标准差为0.05的正态分布,下同。

当τ=0.1时,经过确定性计算可知本系统共有3对反映系统低频振荡的复数根。采用式(24)计算特征根相对于延时的灵敏度,结果见表1。

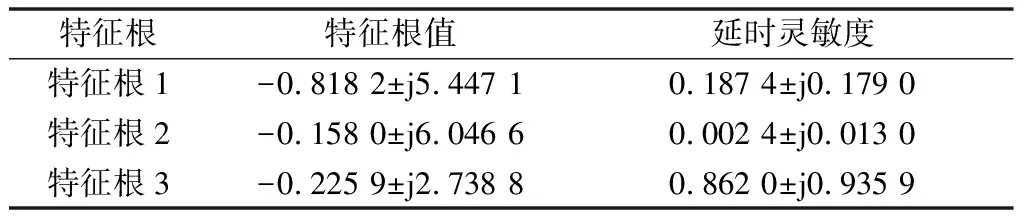
表1　特征根与延时灵敏度Table 1　Eigenvalues and time delay sensitivities

由表1可知,反映局部振荡的特征根1和特征根2对延时的灵敏度指标远小于反映区域间振荡的特征根3对延时的灵敏度指标。表明在延时波动时,特征根3将发生较大的变化,故将特征根3认为是系统的临界特征根,其在随机延时下实部的分布概率可近似地表达整个系统的稳定程度。

采用本文所提方法对考虑随机延时的广域系统临界特征根的概率密度进行计算。具体半不变量与阶距参数以及Gram-Charlier级数的系数见附录B。为了验证计算结果的正确性,提高仿真结果的可信度,本文在搭建的信息物理融合电网系统(cyber-physical power system,CPPS)仿真平台上使用蒙特卡洛模拟进行检验。本文在通信网络仿真软件OPENT中搭建两区四机通信系统模型(见附录A图A2),在其中的广域网络模块中设定通信延时τ～N(0.1,0.052),在MATLAB中搭建对应的电力系统模型并设定蒙特卡洛模拟次数为5 000,从而对通信环节中具有随机延时的电力信息融合系统进行模拟仿真。在联合仿真过程中,为了避免不同软件接口传输延时对仿真计算结果的影响,本文在OPNET与MATLAB仿真程序之间采用完全同步的方式进行联合仿真。采用完全同步的仿真方式时,当MATLAB仿真过程中处于需要获得广域信号延时信息的阶段时向OPNET发送通信请求,此时MATLAB暂停在当前仿真时刻,OPNET开始执行仿真计算,当OPNET获得该次传输数据的延时信息并将所有信息传输给OPNET自带的ESYS接口后,暂停OPNET仿真在当前时刻。ESYS向MATLAB发起通信请求,MATLAB从ESYS的发送结果中获得数据的延时信息后,完成当次计算。保存结果并继续运行到下一次需要用到数据延时信息的时刻,直到结束5 000次蒙特卡洛模拟。

基于Gram-Charlier级数展开的计算方法和采用OPNET-MATLAB联合仿真平台进行5 000次蒙特卡洛模拟仿真,所获得的系统临界特征根实部的概率密度曲线结果如图1所示。

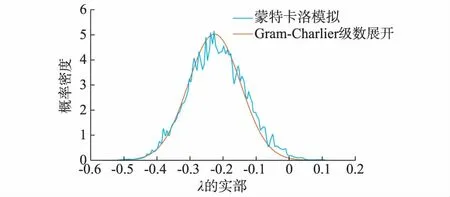
图1　特征根实部的概率密度函数曲线Fig.1　Probabilistic density function curves of real part of eigenvalue

图1显示,使用Gram-Charlier级数展开方法得到的临界特征根实部的概率密度函数曲线和蒙特卡洛模拟得到的结果较为吻合,验证了本文所提计算方法的正确性。

3.2　不同延时特性对小干扰稳定的影响分析

应用本文所提方法对具有不同延时特性的采用广域阻尼控制器的两区四机系统进行小干扰概率稳定计算,得到临界特征根实部的累积分布函数(cumulative distribution function,CDF)的图像,进而分析不同延时特性对系统小干扰稳定的影响。

延时服从正态分布时,不同均值、方差下,系统临界特征根实部的概率累积分布曲线的关系分别如图2(a)和(b)所示。延时服从均匀分布时,不同分布参数下的概率累积分布曲线见附录C图C1。延时服从正态分布(方差为0.05)时,小干扰稳定概率随正态分布均值变化的曲线如图3所示。对图中的结果进行分析后可得到如下结论。

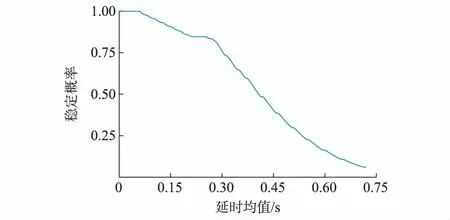
图3　不同延时均值下系统小干扰稳定概率Fig.3　Probability of system small-signal stability with different time delay mean values

1)延时均值对系统临界特征根实部的概率分布有较大影响,且延时均值越大,系统小干扰稳定概率越低,与常规物理理解一致。

2)延时模型的方差变化主要影响了概率累积分布曲线的斜率,即表明当通信延时的波动程度越大时,系统临界特征根实部的分布范围越广,对系统的小干扰稳定越不利。

3)当通信系统随机延时的均值与方差增大时系统的小干扰稳定概率(P(ξ<0))降低,由图3可知,当延时均值为0.735 s时P(ξ<0)=0,此时系统已完全失去小干扰稳定。

3.3　计及随机延时的PSS鲁棒性设计方法验证

使用本文提出的计及随机延时的PSS鲁棒性设计的方法对两区四机系统的广域阻尼控制器进行参数设计。SAPSO优化计算过程中取群落大小为30,学习因子均设置为2.05,退火常数和迭代次数分别取0.5和100。当网络环境处于τ～N(0.15,0.052)的情况下,阻尼控制器的参数设计考虑延时随机特性时,优化目标函数为式(25),求解得到J=-0.062 5,此时控制器参数为T1=T3=0.763 2,T2=T4=0.246 9。如果控制器设计仅考虑延时的均值,即SAPSO的优化目标函数为固定延时(延时为正态分布的均值)下系统的临界特征根具有最小的实部,计算得到控制器参数为T1=T3=0.853 6,T2=T4=0.274 8。若控制器的设计不考虑延时,即SAPSO的优化目标函数传输延时为0时,系统的临界特征根具有最小的实部,此时控制器参数为T1=T3=0.420 2,T2=T4=0.081。

上述3种情况临界特征根实部的概率密度函数曲线和累积分布函数曲线分别如图4和图5所示。

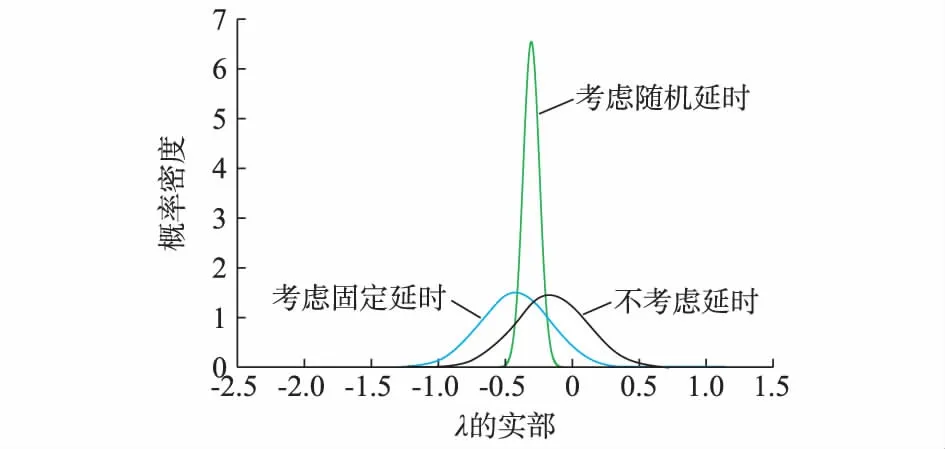
图4　临界特征根实部的概率密度函数曲线Fig.4　Probabilistic density function curves of real part of critical eigenvalue

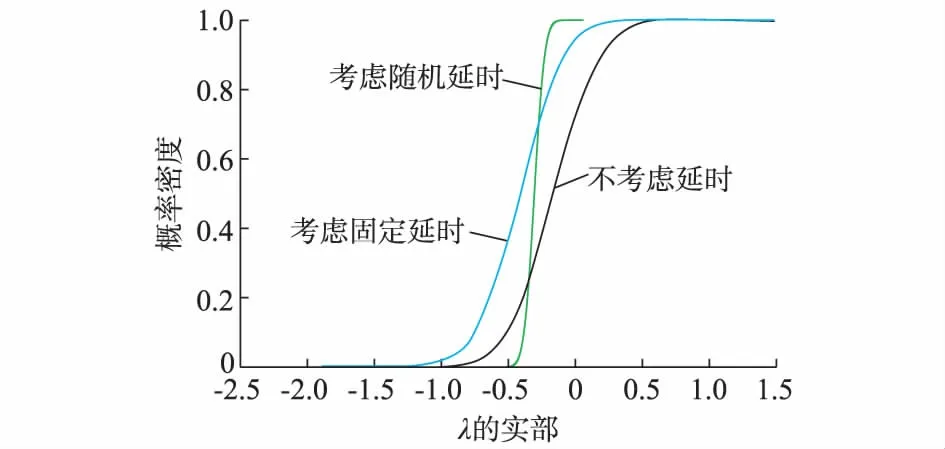
图5　临界特征根实部的累积分布曲线Fig.5　Cumulative distribution function curves of real part of critical eigenvalue

由图5可得,在输入信号具有随机延时的情况下,控制器参数设计不考虑延时,系统临界特征根实部为负的概率为71.88%,系统有28.12%的概率失去小干扰稳定。如果控制器参数仅考虑固定延时,系统临界特征根实部为负的概率为94.1%,系统有5.9%的概率失去小干扰稳定。由此可知,在随机延时情况下,控制器参数设计仅考虑信号固定延时相比于完全不考虑延时,系统小干扰稳定概率已经有较大幅度的提升。进一步,采用本节提出的考虑随机延时的控制器设计方法后,相比于仅考虑固定延时的设计方法,系统的临界特征根实部的均值增大,即此时系统阻尼有所下降,但方差大幅度减小,使得系统临界特征根实部均位于左半平面,此时可认为系统小干扰稳定的概率为100%。这证明了本文提出的计及随机延时的PSS鲁棒性设计方法有效地提高了具有随机延时的电力系统的小干扰稳定性。

4　结语

本文研究了传输延时的随机性对系统小干扰概率稳定的影响,基于阻尼转矩分析法推导了特征根对广域信号延时的灵敏度计算方法,并利用Gram-Charlier级数的方法计算出了系统临界特征根实部的概率密度函数。在获得特征根概率密度函数的基础上,对随机延时下系统的小干扰概率稳定进行了分析。结果表明,当广域信号随机延时具有较大的均值和方差时对系统的稳定性极为不利。最后,对广域阻尼控制器的参数进行了鲁棒性设计,从而提升了系统在随机延时下保持小干扰稳定的概率。在大规模互联电网中应用广域阻尼控制器抑制区域间低频振荡时,采用本文提出的考虑随机分布延时影响的系统小干扰概率稳定性分析方法,可以快速计算出系统小干扰稳定概率,相比于蒙特卡洛模拟具有更好的适用性。

本文研究过程中未考虑多个广域信号的传输延时,也尚未考虑电网拓扑以及运行方式的不确定性。如何利用半不变量的可加性,同时考虑多个相互独立的不确定单元对系统小干扰稳定的影响,以及设计出更好的广域阻尼控制器,都值得进一步研究。

感谢国网江苏省电力有限公司科技项目(J2016015)对本研究的支持与资助。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。