“假设”诚可贵、“证明”价更高
——以一道典型力学试题的正解和错解为例
2018-07-12周来友
周来友
(河北省唐山市丰润区任各庄镇中学 064012)
一、问题呈现
如图所示,质量为M=1.50 kg的物体静止放在台秤上,秤盘的质量为m=1.5 kg,弹簧本身的质量不计,劲度系数k=800 N/m,台秤放在水平面上.现给物体施加一个竖直向上的力F,使物体向上做匀加速直线运动,已知力F在0.2 s内为变力,0.2 s后为恒力,求F的最大值和最小值.
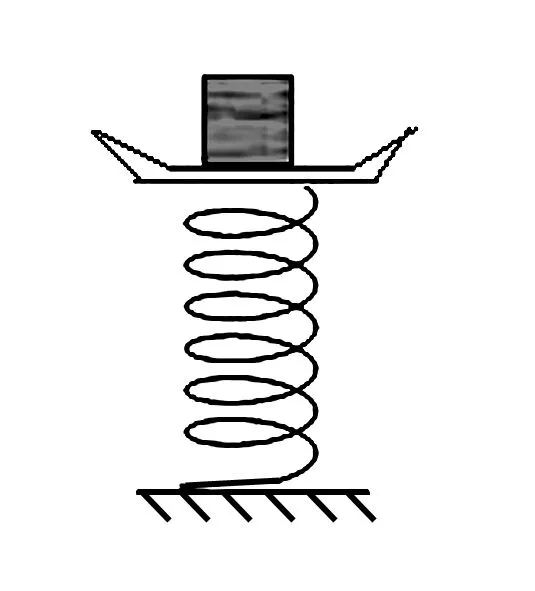
此题乍一看,难度不大.但是,如果不认真审题,不仔细研究已知条件,不能全面把握物体和秤盘的完整运动过程,解答此题未必会顺风顺水.下面,就让我们一起对这道题的错解和正解情况进行品读,从中体会如何应用假设法解答物理问题.
二、错解点评
错解一由题意可知,弹簧在0.2s这一时刻恢复原长,此时,物体和秤盘恰好分离,物体或秤盘运动的位移就等于弹簧静止时被压缩的长度,这一时刻秤盘和物体之间没有弹力,此时F最大.
设匀加速直线运动的加速度为a,由运动学知识可得
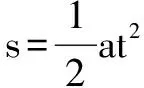
由整个系统静止时总重力等于弹力可得
(M+m)g=Ks②
由①②联立,解得a=7.5 m/s2.
系统刚开始运动时力F最小,最小值为
Fmin=(M+m)a=(10.5+1.5)×7.5N=90N系统运动到0.2秒时,力F最大(以后恒定不变),最大值为
Fmax=M(g+a)=10.5×(10+7.5)N=183.75N
点评认为在0.2 s这一时刻弹簧恢复原长经不起推敲.照此说法,弹簧恢复原长时秤盘所受弹力为零,速度为零,加速度也为零.但此时秤盘在自身重力的作用下,要从速度为零开始向下做加速运动,而物体的加速度不变也不为零,速度还在均匀增加.这意味着物体与秤盘早就在弹簧恢复原长之前早就已经分离.可见,当两者恰好分离的时刻,弹簧并没有恢复原长.
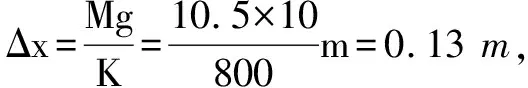
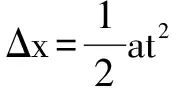
系统刚开始运动时,力F最小,最小值为
系统运动到0.2秒时,力F最大(以后恒定不变),最大值为
点评此种想法距离正确答案只有一步之遥,遗憾的是认为物体运动0.2 s时,弹簧的弹力等于秤盘的重力.照此说法,这一时刻秤盘所受合力为零,加速度也变为零,但物体的加速度并不为零.这意味着物体与秤盘早就在弹簧的弹力等于自身重力之前早就已经分离.可见,两者恰好分离的时刻,弹簧的弹力并不等于秤盘的重力.
以上两种错解的原因主要是:对物体和秤盘在分离前、分离时、分离后的运动过程所包含的受力情况、力的变化、运动的速度和加速度等每个要素如何变化根本不清楚.给人的感觉好像就是通过假设两者分离的临界状态来解答本题.物理需要假设,但假设要有理有据,无根据的假设对解决问题豪无意义.
三、正解分析
1.如果对物体A不施加竖直向上的力F,设弹簧被压缩的长度为x0,则系统受到竖直向上的弹力大小为Kx0.由题意可知,系统处于静止状态时(规定为0时刻,时间记为0),有Kx0=(M+m)g成立.
2.现在给物体施加一个竖直向上的力F以后,由题中对F的限定可知,F必须保证使物体由静止状态变为向上做匀加速直线运动的状态,且物体的加速度始终为a.显而易见,物体由静止动起来的同时秤盘也跟着动起来,只要两者不分离始终就可以看成是一个系统,故分离前秤盘运动的加速度也是a.
3.分离前,在竖直方向上,秤盘受到弹簧给的向上的弹力F弹、自身向下的重力mg、物体给的向下的压力F2这三个力的作用,而物体则受到向上的力F、自身向下的重力Mg、秤盘给的向上的支持力F1这三个力的作用,F1=F2.
4.显然,在整个系统刚刚动起来的瞬间,注意这一时刻可视为0时刻,速度可视为0,时间仍可记为0,弹簧被压缩产生的竖直向上的弹力可视为来不及减小,故其大小仍然等于系统处于静止状态时的弹力,即等于系统的重力,此时刻弹力最大.所以,使物体(或系统)刚好由静止状态运动起来的这一时刻,力F的值最小.找准研究对象采用整体法或隔离法进行受力分析,并由牛顿第二定律可得,最小值等于(M+m)a.请看下面的证明.
证明一:用隔离法和整体法
在0时刻,Kx0=(M+m)g,相互作用力F1=F2.由牛顿第二定律得
对物体:F+F1-Mg=Ma①
对秤盘:Kx0-F2-mg=ma②
由①②相加可得,F=(M+m)a.
证明二:用整体法
把物体和秤盘看成一个系统,由牛顿第二定律得
F+Kx0-(M+m)g=(M+m)a,
因为系统刚刚动起来时Kx0=(M+m)g,所以F=(M+m)a.
5.已知力F在0.2s内为变力,F在0.2s内究竟是逐渐变大还是逐渐变小?因整个系统向上运动,弹簧弹力因弹簧的伸长会逐渐减小,而加速度a不变,所以对整个系统利用牛顿第二定律进行分析可知,力F在0.2s内逐渐增大.
证明:对整个系统,由牛顿第二定律可得
F+F弹-(M+m)g=(M+m)a,

因为a、M、m、g是常数,所以F+F弹也是常数.又因为F弹在不断减小,所以F逐渐增大.
6.既然力F在0.2s内逐渐增大,而物体的加速度又始终保持不变,当然包括在0.2s内物体所受合力的大小、方向始终保持不变,即便以后F变为恒力,物体和秤盘分离时也是如此.这就出现了一个问题:在0.2s内,物体和秤盘之间的相互作用力F1(或F2)怎样变化?再次利用牛顿第二定律进行分析可知,F1(或F2)应该是逐渐减小.
证明:对物体A,由牛顿第二定律可得
F+F1-Mg=Ma,
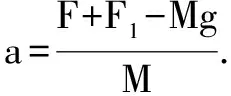
因为a、M、g是常数,所以F+F1是常数.
因为F逐渐增大,所以0.2 s内F1(或F2)逐渐减小.
7.分析至此,我们对已知条件“力F在0.2 s内为变力,0.2 s后为恒力”进行探讨,而这也正是解答本题的关键所在.在0.2 s这一时刻将会是一种怎样的情形呢?采用假设法并结合牛顿第二定律进行分析可知,物体和秤盘只能是在0.2 s这一时刻恰好分离;当然,借助数学极限或是微积分的思想也能猜出此时刻两者分离.除此之外别无二选,否则会和已知条件相悖;也会和前面得出的0.2 s内F1(或F2)逐渐减小,力F在0.2 s内逐渐增大这些结论相悖.为了叫大家对用假设法分析问题引起足够的重视,笔者仍想做以下陈述.
证明:假设物体和秤盘在0.2s这一时刻不分离,接下来我们分两种情况展开推理.
①设两者在t0s(t0<0.2)时分离.此时物体只受向上的力F和向下的重力Mg两个力的作用,加速度为a.由牛顿第二定律可得,F=Ma+Mg.很显然F是一个常数,这说明力F在t0s(t0<0.2)内为变力,在t0s(t0<0.2)及其以后为恒力.这和已知条件“力F在0.2 s内为变力,0.2 s后为恒力”相矛盾.故假设不成立.
②设两者在t0s(t0>0.2)时分离.同理可证假设不成立.
既然假设不成立,说明两者就在0.2 s这一时刻恰好分离.
8.在0.2 s之前,它们之间的相互作用力F1、F2是逐渐减小的,力F是逐渐增大的.因此,借助数学极限或是微积分的思想,不难猜出在0.2 s时,F1、F2减小到零,而F增大到最大.当然,采用假设法并结合牛顿第二定律进行分析也会得到同样的结论,证明从略.
分离时,物体只受竖直向上的力F和自身重力这两个力的作用(注意加速度依然为a),由牛顿第二定律不难得出,此时力F的最大值为M(g+a).0.2 s后,力F以最大值作为恒力不变.
证明:在0.2 s这一时刻,物体与秤盘恰好分离时,此时对物体,由牛顿第二定律可得,F-Mg=Ma,解得F=M(g+a).
9.分离时,秤盘只受向上的弹力F弹和自身重力mg这两个力的作用,分离后显然如此.只是分离后,即0.2 s后,弹簧在逐渐伸长,弹力在逐渐减小,则秤盘所受合力自然也逐渐减小,导致秤盘的加速度逐渐减小,以后会减小到零,那时速度达到最大;可在0.2 s以前,秤盘B加速度一直为a.因此,我们仍然借助于数学极限或是假设法等思想,不难得出在0.2 s这一时刻秤盘B加速度依然为a的结论,证明从略.
10.分离以后,即0.2 s以后,物体继续向上做加速度为a的匀加速直线运动.而秤盘一开始也做向上的加速运动但不匀速,这是因为弹簧弹力在逐渐减小.随者运动的持续进行,当秤盘第一次运动到弹簧弹力减小到等于自身重力时,合力、加速度第一次变为零,此时速度第一次达到最大值,这一时刻的位置称为平衡位置.再后来,秤盘以平衡位置为中心,上下来回做简谐振动.而简谐振动第一次瞬时停止的那一时刻,弹簧恰好恢复到原来的长度.
值得一提的是:本题之所以做如此详细的分析,目的有三个,一是全方位进行审题,理解本题;二是是叫人们认识到,解决物理问题在很多情况下是需要假设,但假设必须做到有理有据,有理论作支撑,有事实做后盾;三是提醒大家要善于借助数学上的极限(无限逼近)、积分、反证法等数学思想,增加对“时刻”这一物理概念和常用的假设法的真正理解;四是真正理解“牛顿第二定律”这一重要物理规律.
四、正解点评
为了便于动笔解答本题,我们把上面的分析过程,做一个简要总结:
使物体A(或系统)刚好由静止状态运动起来的这一时刻(零时刻,时间记为0),Kx0=(M+m)g依然成立,此时加速度为a,力F的值最小,最小值等于(M+m)a.
题设对F的限定条件,决定了物体和秤盘分离的临界状态就在0.2 s这一时刻.此时,两者之间的相互作用力减小到零;两者的加速度依然为a,即弹簧的弹力和秤盘的重力的合力使秤盘产生的加速度,等于拉力F和物体的重力的合力使物体产生的加速度;力F增大到最大值,以后不再变化,最大值是M(g+a).
到此说明,求出加速度a成为了解决问题的关键.注意分离时,系统从静止刚刚动起来时(0时刻)到0.2 s这一时刻,运动的位移s等于弹簧静止时(零时刻)被压缩的长度x0减去0.2 s这一时刻弹簧被压缩的长度x.利用运动学位移公式和牛顿第二定律,对整个系统、物体、秤盘等研究对象轮番探索,横向纵向比较反映物理规律的关系式子,即可求出加速度a,从而使问题得到解决.
至于其它信息,比如0.2 s以后,秤盘B做简谐振动;弹簧恰好恢复到原来的长度;弹簧的弹力等于秤盘的重力;等等.这些信息和分析问题有关,但和动笔解题一点关联没有,不再累述.正因如此,我们的计算必须紧紧围绕0.2 s这一时刻展开作答.
正解一以位移公式为中心求解
设0.2 s这一时刻,弹簧被压缩的长度为x,对秤盘B,根据牛顿第二定律可得
Kx-mg=ma①
对整个系统,由静止刚动起来时(0时刻)有
Kx0=(M+m)g②
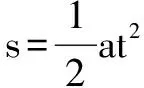
由①②③式可得

刚起动时,F的值最小,最小值为
Fmin=(M+m)a=(10.5+1.5)×6 N=72 N.
0.2 s时,物体A与秤盘B恰好分离,此时F的值最大,最大值为
Fmax=M(g+a)=10.5×(10+6)N=168 N.
正解二以整个系统为中心求解
设0.2 s这一时刻,弹簧被压缩的长度为x,秤盘B和物体A运动位移是s,系统刚刚启动时弹簧被压缩的长度为x0,显然x=x0-s.
0.2 s时,对物体A,根据牛顿第二定律可得
F-Mg=Ma①
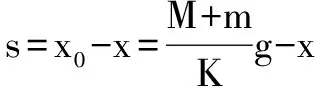
对系统,根据牛顿第二定律可得
F+Kx-(M+m)g=(M+m)a③

把①④代入③整理可得

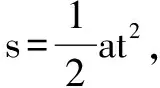
0时刻,系统刚起动时,F的值最小,最小值为
Fmin=(M+m)a=(10.5+1.5)×6N=72N.
0.2s时,物体A与秤盘B分离,F的值最大,最大值为
Fmax=M(g+a)=10.5×(10+6)N=168N.
正解三以弹力式子为中心求解
设0.2s这一时刻弹簧被压缩的长度变为x,秤盘B和物体A运动位移是s,系统刚刚启动时弹簧被压缩的长度变为x0,显然x=x0=s.则0.2s时弹力的大小为
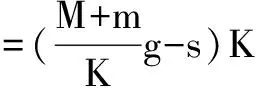
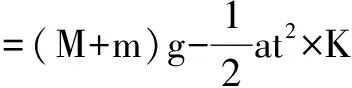
0.2 s时物体A与秤盘B分离,对秤盘B,根据牛顿第二定律可得F弹-mg=ma②
由①②解得a=6 m/s2.
0时刻,系统刚起动时,F的值最小,最小值为
Fmin=(M+m)a=(10.5+1.5)×6N=72N.
0.2s时,物体A与秤盘B分离,F的值最大,最大值为
Fmax=M(g+a)=10.5×(10+6)N=168N.
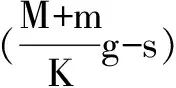
通过对这道试题的正误解答及分析,我们理应受到这样的启示:认真审题,抓住最有价值的信息进行大胆假设;准确理解物理概念;选准研究对象,利用最重要的物理规律对解决问题所涉及到的方方面面,进行层层剖析;根据生活经验和学过的数学、物理等知识,对问题做出合理的假并寻求理论支撑,进行小心求证,这些才是解决物理问题的王者之道,正所谓“假设”诚可贵、“证明”价更高.
