Reversible Natural Language Watermarking Using Synonym Substitution and Arithmetic Coding

LingyunXiangYanLiWeiHao3PengYangandXiaoboShen

Abstract:For protecting the copyright of a text and recovering its original content harmlessly, this paper proposes a novel reversible natural language watermarking method that combines arithmetic coding and synonym substitution operations. By analyzing relative frequencies of synonymous words, synonyms employed for carrying payload are quantized into an unbalanced and redundant binary sequence. The quantized binary sequence is compressed by adaptive binary arithmetic coding losslessly to provide a spare for accommodating additional data. Then, the compressed data appended with the watermark are embedded into the cover text via synonym substitutions in an invertible manner. On the receiver side, the watermark and compressed data can be extracted by decoding the values of synonyms in the watermarked text, as a result of which the original context can be perfectly recovered by decompressing the extracted compressed data and substituting the replaced synonyms with their original synonyms. Experimental results demonstrate that the proposed method can extract the watermark successfully and achieve a lossless recovery of the original text. Additionally, it achieves a high embedding capacity.

Keywords:Arithmetic coding, synonym substitution, lossless compression, reversible watermarking.

1 Introduction

With the rapid development of computer and network technologies, the security of digital contents is attracted increasing academia and industry attentions over the world.Watermarking technique is one of the prominent solutions of protecting the copyrights of digital contents. In recent years, deep learning has been successful in various fields and also has achieved good results in the field of digital watermarking [Kandi, Mishra and Gorthi(2017)]. Unfortunately, in order to ensure the security of digital contents, watermarkingalways embeds the watermark into a cover carrier in a visible or invisible way, so that the sensitive information in the cover carrier may be damaged. But, in some fields, such as military, medicine, etc. any modification, even slightest distortion, is intolerable to be made into the cover carrier. Consequently, reversible watermarking techniques [Khan,Siddiqa, Munib et al. (2014)] are widely used in these fields, which can satisfy the strong requirement of recovering the watermarked carrier to its original form.

Reversible watermarking can be considered as a special case of watermarking, which can not only extract the embedded watermark successfully, but also restore the original carrier completely. Currently, it has gained more and more attentions in military communication, healthcare, governmental security communication, and law-enforcement.However, researches on reversible watermarking mainly focus on taking images as carriers, and there are relatively few researches for text data [Liu, Sun, Liu et al. (2010);Jiang and Chen (2010); Fei and Tang (2013)].

The existing text reversible watermarking methods mainly have two problems: Low watermark embedding capacity and large amount of being shared additional information.To solve these two problems, this paper proposes a reversible natural language watermarking method based on adaptive binary arithmetic coding from the perspective of lossless data compression.

The proposed method first encodes only two words with the largest word frequencies in each synonym set, thereby achieving binarization of synonyms appearing in the cover text. Since the number of synonyms with relatively high frequencies in the cover text is far more than that of synonyms with relatively low frequencies [Xiang, Sun, Luo et al.(2014); Hu, Zuo, Zhang et al. (2017)], the binary sequence derived from quantizing the synonyms in the cover text is severely nonuniform, so that there is large redundant space for providing the possibility of compression. From this view, adaptive binary arithmetic coding is selected to compress the binarized synonym sequence losslessly. Then, the compressed binarized synonym sequence appended with the watermark and some additional information is embedded into the cover text by synonym substitutions. The watermark is extracted by decoding the values of synonyms in the watermarked text, and meanwhile the original synonyms can be recovered by decompressing the extracted compressed data using arithmetic coding. With comprehensive experimental results, the proposed method has been proved with considerable embedding capacity, which makes it practical and useful. The key of the proposed method is to compress the original synonym sequence losslessly and effectively, which has two contributions:

(1) A large spare space can be provided by compressing the cover synonyms, which can be employed for accommodating additional data and embedding the watermark information. The higher the compression performance obtained by the employed compression algorithm is, the larger the watermark embedding capacity is;

(2) Only the watermarked text is required for extracting the watermark and recovering the original cover text without any extra auxiliary information. The decompression of the compressed binarized synonym sequence can directly recover the original cover text losslessly, as the decompressed result represents the encoded values of original synonyms in the cover text, although original synonyms are changed during embedding information.

The rest of the paper is organized as follows. Section 2 discusses the related works of reversible watermarking. Section 3 analyzes synonym quantization and introduces how to effectively compress the quantized synonym sequence by adaptive binary arithmetic coding. In Section 4, the proposed reversible watermarking method is described in detail.Section 5 gives experimental results and analysis.

2 Related work

2.1 Reversible watermarking

Reversible watermarking, also known as lossless watermarking, is one of the promising solutions for protecting copyright and digital content, which allows extracting the embedded watermark information along with the lossless restoration of original cover carrier. Over the past few years, many researchers have carried out researches on reversible watermarking, which are mainly classified into five major categories: (1)integer transforms-based; (2) pixel prediction-based; (3) histogram modification-based;(4) frequency domain-based; (5) data compression-based.

Integer transform-based reversible watermarking method [Cao and Van At (2016)]converted two adjacent pixels in an image block into two new pixels by using an invertible integer transform for embedding watermark. The original pixels can be recovered by using the new pixels. The most typical invertible integer transform was difference expansion [Hu, Lee, Chen et al. (2008)]. In this transform, the difference between two adjacent pixels was increased by two times and added a watermark bit to generate a new difference. With the new difference and the mean of two original adjacent pixels, two new pixels embedded a watermark bit were generated and can be employed to recover the original pixels. This kind of methods achieves high embedding capacity and low computational complexity.

Pixel prediction-based method utilized prediction error for recovering the original image.It predicted a current pixel by the correlation among its adjacent pixels. According to the watermark bit, the current pixel was modified to adjust prediction error between predicted pixel and the true pixel [Dragoi and Coltuc (2016)]. Its embedding capacity achieved approximately one bit per pixel. However, it was easy to cause some pixels overflow or underflow. Thus, a location map was created to identify the selected expandable locations, which can undergo prediction-error expansion without overflow or underflow [Kamstra and Heijmans (2005)]. The performance had been improved, but it required more auxiliary data.

In approaches of histogram modification-based reversible watermarking, an image was divided into several blocks, each of which was split into two zones for calculating the corresponding histograms. The watermark can be embedded by shifting the lowest bin to the highest one or shifting the highest bin to the lowest one [Coatrieux, Pan, Cuppens-Boulahia et al. (2013); Yadav and Naskar (2016)], while the original image can be recovered from the watermarked image without any loss. These methods have low computational complexity and distortion.

Frequency domain-based methods employed various transforms, such as wavelet transform, discrete cosine transform, etc. to transform the cover carrier from spatialdomain to frequency domain. They modified frequency coefficients to achieve the purpose of embedding the watermark [Lee, Chang and Kalker (2007)]. Inverse transform was employed to extract watermark and recover the original image. These methods can provide higher image quality and achieve better robustness than spatial domain-based methods.

Data compression-based methods generally compressed a part of cover image, which was essential for the recovery of original image, and embedded the compressed information along with the watermark [Zhang, Chen and Yu (2012)]. A well-known compressionbased method was proposed by Celik et al. [Celik, Sharma, Tekalp et al. (2005)]. It first quantized the intensity values of pixels in the cover image and compressed the remainders, which were susceptible to embedding distortion, using a context based adaptive lossless image code. The compressed descriptions concatenated with watermark information were embedded into the cover image. A prediction-based conditional entropy coder was utilized to improve the embedding capacity. Consequently, Xuan et al. [Xuan,Yang, Zhen et al. (2005)] proposed a reversible watermarking with increased embedding capacity by utilizing a companding function to compress integer wavelet coefficients.However, it increased the auxiliary data for exactly recovering the original cover image upon extraction of the embedded information. There are more researches on improving embedding capacity by combining compression method with other techniques.

2.2 Reversible natural language watermarking

Most existing reversible watermarking methods were taken pixels in images as host signal, which were totally different from text data. Due to the particularity of natural language, there are relatively few researches on natural language reversible watermarking.Liu et al. [Liu, Sun, Liu et al. (2010)] firstly proposed a text reversible watermarking method, which converted the convertible words or sentences in the original text into integers, and then employed an improved integer transform and difference expansion to embed the watermark into the cover text. Compared with image reversible watermarking methods, its overflow/underflow problem is quite serious. As the range of pixel values in a gray image can be [0, 255], the predicted pixel value is often very similar to the original one, which has a relative low probability to be a boundary value. Thus, it has a relative low probability of causing overflow/underflow. While the range of the integers converted from convertible words or sentences is extremely narrow. The probability that a converted integer is a boundary integer is quite high, so it is easy to have an overflow or an underflow caused by the predicted integer obtained from the context. As a result, the embedding capacity would be greatly reduced.

Consequently, Jiang et al. [Jiang and Chen (2010)] proposed a robust reversible watermarking method for text data. This method analyzed collocation of words in a same context by dependency syntax. The synonym with the highest degree of collocation than its synonymous words was selected and made XOR operation with the original one. The result of XOR operation was used as a recovery parameter to vote for extracting the watermark. However, a large amount of redundant space was required to store the original data for cover text recovery.

Fei et al. [Fei and Tang (2013)] improved the method proposed by Liu et al. [Liu, Sun,Liu et al. (2010)]. Their proposed method performed contextual syntactic analysis on synonyms to select substitutable synonyms within a threshold for embedding watermark and reducing semantic distortion. At the same time, with predicting the current suitable synonym based on the context, the method used the prediction error expansion to embed watermark, while the overflow/underflow information was mapped into a chaotic sequence so that the synonyms can carry more watermark information. As a result, the method improved embedding capacity. Although this method successfully solved the overflow/underflow problem generated by synonym prediction, it needed to share a large amount of auxiliary data between the receiver and the sender to recover original synonyms.

Aiming at the improvement of embedding capacity and the reduction of auxiliary data,this paper proposes a compression-based reversible natural language watermarking method. The original synonyms in the cover text are quantized into a binary sequence,which will be compressed by adaptive binary arithmetic coding. The compressed data and few auxiliary data related to its length and watermark length are treated as a part of the embedded payload, which are embedded by substituting synonyms. By decoding the synonyms in the watermarked text, the embedded information can be extracted for obtaining the watermark and recovering the original synonyms without any distortion.

3 Synonym quantization and compression

3.1 Synonym quantization

There are many ways to embed watermark into cover texts, which are mainly divided into two main categories: Format-based method, e.g. adjusting the font format of invisible spaces [Kumar, Malik and Singh (2017)]; content-based method, e.g. using synonym substitutions [Topkara and Atallah (2006)], and syntactic transformations [Meral, Sankur,Sumru et al. (2009)]. Content-based method is also called natural language watermarking or linguistic watermarking. The synonym substitution-based watermarking, compared to syntactic transformation-based one, has a relative larger embedding capacity and better imperceptibility, and requires relative simple natural language processing techniques.Because of its simple implementation and good performance, it is widely used for covert communications and copyright protection.

For synonym substitution-based watermarking, a synonym database must be prepared to recognize synonyms in the cover text. And then, synonym quantization rules are designed to encode the synonyms into a digital sequence to guide the watermark embedding.Synonym quantization rules are very important, which directly determine the performance of subsequent watermark embedding.

Currently, there are a variety of different synonym coding rules used in existing steganographic and digital watermarking methods. The steganography proposed by Yajam et al. [Yajam, Mousavi and Amirmazlaghani (2014)] transformed the synonyms into random numbers ‘0’ or ‘1’ through a pseudo-random function. Bolshakov[Bolshakov (2004)] directly encoded a synonym according to its position locating in the corresponding synonym set. Chiang et al. [Chiang, Chang and Hsieh (2003)] constructed

a binary tree for each synonym set and encoded each synonym as a variable-length codeword by assigning ‘0’ or ‘1’ to different branches. The above coding methods treat synonyms in the same synonym set equally and encode them independently.

Although synonymous words are linguistically similar, there may exist significant statistical differences. In general, semantically similar words are not equally distributed in a corpus. Due to the influence of language habits, context, etc. some words are used frequently, while their synonymous words are used infrequently. From the view of word frequencies, many researchers presented adaptive synonym coding method for steganography or watermarking methods to improve their performance. Lin et al. [Lin,Tang and Wang (2015)] performed Huffman coding based on relative frequencies of synonyms, such that a synonym with higher frequency has a shorter codeword than its synonymous word with lower frequency. Thus, the quality of the watermarked text can be improved, as the synonym with higher frequency is likely to load more watermark information. Xiang et al. [Xiang, Wang, Yang et al. (2017)] utilized a similar method to quantize synonyms. In a synonym set, the most frequently used synonym was encoded as bit ‘0’, while the remainders were all encoded as bit ‘1’. As a result, the sequence of encoding synonyms in the cover text is no longer randomly and evenly distributed, but has obvious statistical characteristics, e.g. the occurrences of bit ‘0’ are much larger than those of bit ‘1’.

Set a synonym setSSincluding synonymous wordsss0,ss1,...,ssn−1, wheref(ss0) ≥f(ss1) ≥ ...≥f(ssn−1), andf(ssi)denotes the word frequency ofssi, the encoding result of using the method in Xiang et al. [Xiang, Wang, Yang et al. (2017)] can be described as Eq. (1).

According to Shannon’s information theory, the more uneven the distribution of information elements, the smaller the information entropy is, and the larger the compressible space is; the more uniformly distributed the information elements, the larger the information entropy is, and the smaller the compressible space is. Therefore,the synonym sequences obtained by Eq. (1) can be effectively compressed by an efficient compression algorithm.

As one target of this paper is recovering the original cover text by extracting the compressed quantized original synonyms sequence. By the coding method described with Eq. (1), a bit ‘1’ in the quantized original synonyms sequence may indicate several original synonyms resulting in a fail of exact recovery of the original text. Thus, we propose an improved coding method for synonym quantization.

The synonym that has the highest frequency among the words with the similar meaning in a synonym set is called MFS (Most Frequent Synonym), while the synonym that has the second highest frequency in the synonym set is called SMFS (Second Most Frequent Synonym).

Definition 1The synonym quantization rule proposed in this paper is defined as: If a synonym in a synonym set is a MFS, it will be encoded as ‘0’; if it is a SMFS, then it will be encoded as ‘1’; else it is treated as a normal word without encoded value.

According to Definition 1, the encoding result of synonym quantization is shown in Eq.(2). After encoding all synonyms in a cover text by Eq. (2), a binary sequence will be obtained.

3.2 Compression by adaptive binary arithmetic coding

We define Ratio of MFSs as the ratio of the number of MFSs to the total number of MFSs and SMFSs in a text in this paper. The ratios of MFSs in 100 sample cover texts, which are randomly selected from the cover text sets in the experiments, are displayed in Fig. 1.It can be seen that the ratios of MFSs in cover texts are always more than 0.6, which are concentrated in range of 0.7 to 0.9. Obviously, the number of MFSs is more than that of SMFSs in a cover text. Therefore, the binary sequence composing of the encoded values of MFSs and SMFSs according to Definition 1 should have compressible space to be effectively compressed to a shorter binary sequence.

Figure 1: Ratios of MFSs in the sample cover texts

There are many sources coding methods to compress the source signal, such as Shannon coding, Fano KLT and other orthogonal transformation coding, Huffman coding,arithmetic coding, etc. Huffman coding has high coding efficiency, fast computing speed,and flexible implementation, but it is not good at encoding binary sequence [Howard and Vitter (2002)]. On the contrary, the arithmetic coding, which is a non-blocking coding method, is superior in most respects to Huffman coding [Witten, Neal and Cleary (1987)].Arithmetic coding is one of the most popular entropy coding techniques, and the length of its generated codewords can be approximate the information entropy. Particularly, it is more suitable for compressing binary source signal with higher compression performancecompared with other entropy coding methods. Therefore, this paper employs arithmetic coding to compress the binary synonym sequence quantized by Eq. (2) for providing large spare space to accommodate watermark information.

The basic principle of arithmetic coding is to generate a number within an interval of real numbers [0, 1) as the codeword that represents the input symbols. The longer the input message is, the smaller the interval of the encoding representation, indicating that the more binary bits of the generated number in this interval are. The process of arithmetic coding can be briefly described as following.

Firstly, arithmetic coding segments the interval [0, 1) as many subintervals according to the number of symbols in the alphabet. The ranges of the subintervals are commonly determined by the probabilities of the symbols. Given the alphabet including symbolsa,b,c, ..., the cumulative mass functionF(x)ofx, then the ranges of the subintervals can be calculated sequentially as [0,F(x=a)), [F(x=a)，F(x=b)), …... The different symbols in the message will be encoded by selecting the corresponding subintervals, e.g. the symbolawill select the first subinterval. Secondly, the interval segmentation and subinterval selection are repeated within the selected subinterval for the following symbols. Finally, any number within the final subinterval can be selected to be the result codeword, which can be employed in the reverse procedure to decode the original message.

A great deal of researches have been conducted on arithmetic coding. When the sources contain only two symbols, we call it binary arithmetic coding. Binary arithmetic coding has been widely used in multimedia compression standards, such as MQ coding in JPEG2000, and context-adaptive binary arithmetic coding in H.264 [Xiang, Sun and Fu(2016)]. Whether the probability of each symbol in the alphabet is predetermined or not,arithmetic coding can be fixed or adaptive [Boulgouris, Tzovaras and Strintzis (2001)). In fixed arithmetic coding, by counting frequency of each possible symbol in representative samples of the input messages to be encoded, their probabilities are determined and assigned to possible symbols for coding. The predetermined probabilities should be shared with the encoder and decoder. Alternatively, adaptive arithmetic coding treats each message as an independent unit and changes the probability of each symbol with each symbol transmitted. A statistical probability model is required to update the probabilities of possible symbols adaptively and dynamically. And the decoder updates the probability of each received symbol in precisely the same manner with the encoder.

An adaptive arithmetic coding achieves more significant compression than the fixed one.In this paper, we employ the adaptive arithmetic coding to compress the binary sequence derived from quantizing the synonyms in the cover text. As a result, the binarized synonym sequence is encoded into a shorter binary sequence, which is converted from an arbitrary number within an estimated interval of real numbers [0, 1).

(1) The encoding process of adaptive binary arithmetic coding

The encoding process of adaptive binary arithmetic coding is illustrated by Fig. 2. There are only two symbols ‘0’ and ‘1’ in the alphabet, whose probabilities are dynamically updated every time after transmitting a symbol. Denote the occurrences of symbol ‘0’ and

‘1’ in the transmitted message asC0andC1, respectively; their probabilities asp0andp1; the range of an interval as [RL,RH).

At the beginning, although the probability of each symbol is unknown, it can be regarded that each symbol has an equal probability. Thus, bothC0andC1are initialized to 1, and[RL,RH)is initialized to [0, 1). Then, the initialized cumulative occurrences isC0+C1=2,

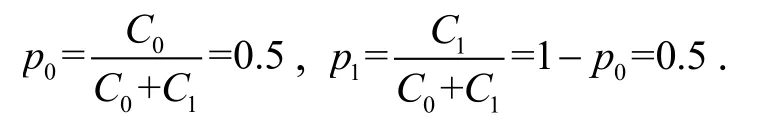
When the encoder receives a source symbol, it calculatesRM=RL+(RH−RL)×p0, the interval [RL,RH)will divided into two subintervals: [RL,RM)and [RM,RH). If the received symbol is ‘0’, the subinterval [RL,RM)is selected as the new interval, whileRHis updated toRM,C0is increased by 1,p0andp1are updated withC0. If the received symbol is ‘1’, the subinterval [RM,RH)is selected as the new interval, whileRLis updated toRM,C1is increased by 1,p0andp1are updated withC1. This procedure is repeated for the following symbols.

At the end, an arbitrary numberNein the final subinterval is selected and converted into a binary sequence to represent the input message.

Figure 2: The compression process of adaptive binary arithmetic coding

(2) The decoding process of adaptive binary arithmetic coding

It is a reverse procedure of the encoding process. The decoder receives a binary sequence and converts it to a numberNe. Firstly, the decoder performs the same initializations as the encoder. Secondly, the decoder calculatesRM=RL+(RH−RL)×p0. IfNefalls into subinterval [RL,RM), then a symbol ‘0’ is obtained and [RL,RM)is selected to the new interval [RL,RH).C0is increased by 1,p0andp1are updated withC0. IfNefalls into subinterval [RM,RH), then a symbol ‘1’ is obtained and [RM,RH)is selected to the newinterval [RL,RH).C1is updated to be increased by 1,p0and p1 are updated withC1.This procedure is repeated until all the original symbols are decoded.

4 Reversible watermarking using arithmetic coding

By adaptive binary arithmetic coding, the encoded values of synonyms in the cover text can be compressed, which can be decompressed in a lossless way to recover the original synonyms. If the compressed binary sequence is embedded along with the watermark information into a cover text, the cover text can be reversibly recovered from the watermarked text. As each synonym can be embedded into one-bit information at least,when the compressed binarized synonym sequence added the binarized watermark information is shorter than the original binarized synonym sequence in the cover text,they can be successfully embedded by synonym substitutions.

The compression ratio is defined as the ratio of the length of the compressed information to the length of the original information. The lower the compression ratio is, the shorter the compressed binary sequence is, and the longer the watermark information can be embedded. Based on above analysis, we propose a reversible watermarking method mainly including two processes: Watermark embedding process and process of watermark extraction and original cover text recovery.

4.1 Watermark embedding

The information embedding process finishes to generate the watermarked text, which is embedded the compressed synonym sequence along with the watermark information.This process is shown in Fig. 3, which can be described as following:

Step 1: Synonym recognition. By traversing the cover text and retrieving a prepared synonym database, if a word is a MFS or a SMFS, it is recognized as a synonym.

Step 2: Binarization. The recognized synonyms are quantized into a binary sequence in terms of the synonym quantization rule defined in Definition 1. If there arensynonyms,an-bit synonym sequenceQis obtained.

Step 3: Compression.Qis compressed into a shorterm-bit binary sequenceQ'by employing adaptive binary arithmetic coding introduced in Section 3.2. Thus, some redundant space can be provided to accommodate the additional watermark information.Step 4: Watermark information binarization. The watermark information is also converted into a binary sequenceMaccording to ASCII values of its characters. Denote the bit length ofMislw.

Step 5: Additional information estimation. In order to distinguish the compressed synonym sequenceQ'from the watermark informationMwhen they are concatenated to be embedded into the cover text, their lengths should be recorded for receivers. As synonyms in the cover or watermarked text are determined and always easy to be counted,nis known for the sender and receiver. The compressed sequenceQ'must be shorter thanQto successfully embed watermark information, namely,m＜n. Thus, we can estimate that the space required to store the length of the compressed synonym sequencemdoes not exceedbit. Under the similar reason,bits should be allocated to store the binarizedlw. Setthus,labits are used to carry the additional information including the length of the compressed synonym sequence and the length of the watermark information.

Step 6: Embedded information generation. The additional information is concatenated withQ'andMto form a complete embedded informationS. There aresynonyms without carrying embedded information. Ifthe embedding will fail.

Step 7: Comparison. The embedded informationSis compared with the original binarized synonym sequenceQ. The values of some corresponding positions are mismatched. Namely, the encoded value of a synonym is not the same with the corresponding embedded information bit.

Step 8: Synonym substitution. For a mismatched position, the original synonym will be replaced by its synonymous word, whose encoded value equals to the embedded information bit. No substitution is done on the matched position. When all the embedded information bits are finished to be embedded, the watermarked text is generated.

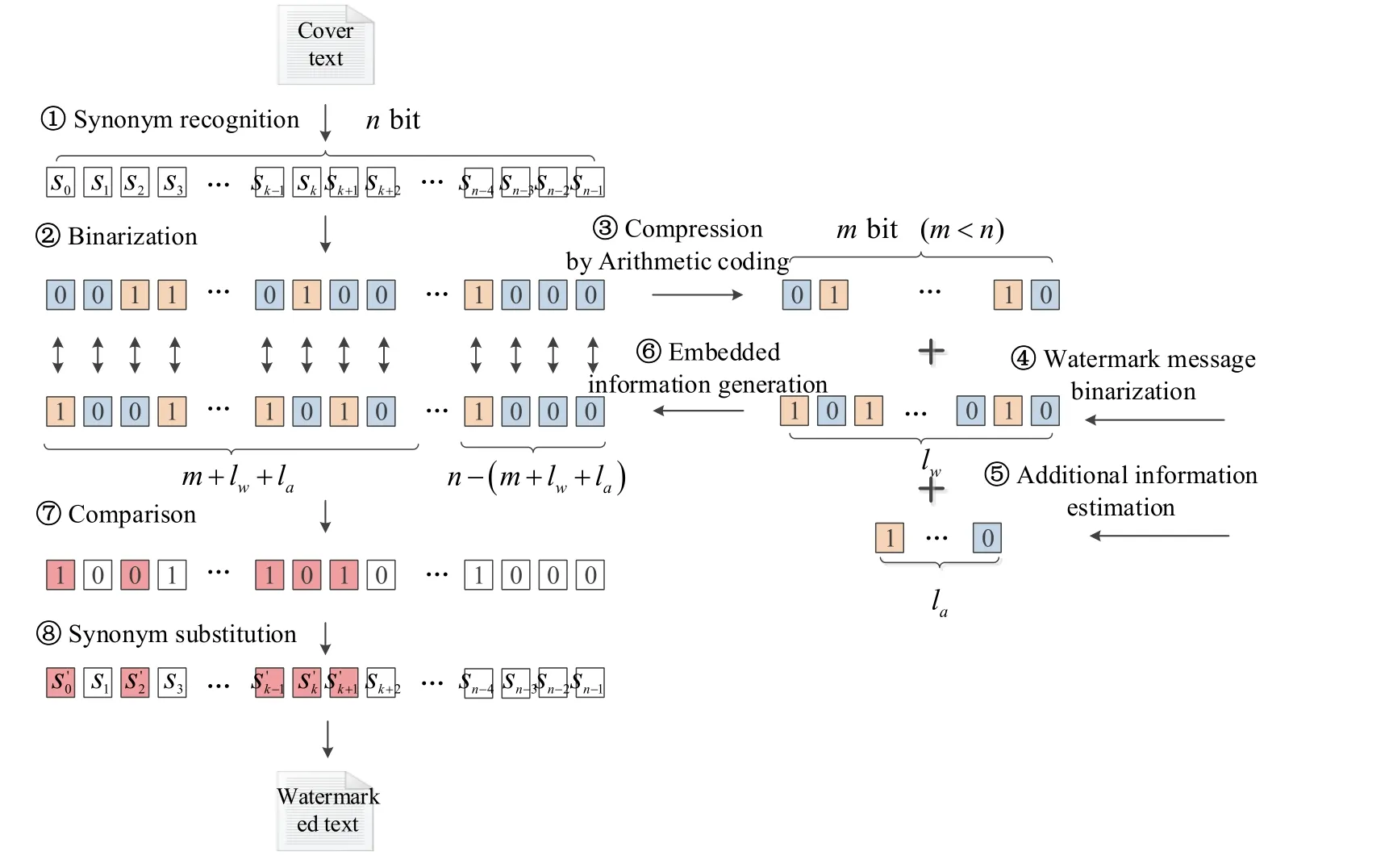
Figure 3: Watermark embedding process

4.2 Watermark extraction and cover text recovery

The watermarked text will be sent to the receivers, who can extract the watermark information and recover the original cover text without any distortion. The process of

watermark extraction and cover text recovery is shown in Fig. 4, which includes six main steps. Step 1 and Step 2 are the same as those in the watermark embedding process.

Step 1: Synonym recognition. The synonyms in the watermarked text are recognized.

Step 2: Binarization. The synonyms are encoded into a binary sequence'Sby Definition 1.

Step 3: Division of the binarized synonym sequence. By counting the number of synonyms being denoted asn, the firstbits of'Sis obtained and expressed as a decimal numberm, which represents the length of compressed synonym sequence. Consequently,the length of the watermark informationwlis computed by reading the nextbits of'S.mandwlare the additional information. Then, reading the nextmbits of'S, the compressed synonym sequence'Qis extracted. Going on reading the nextwlbits of'S, the binarized watermark informationMare extracted.

Step 4: Watermark information extraction. The watermark information is extracted by convertingMinto characters.

Step 5: Decompression. The original binarized synonym sequenceQcan be recovered by decompressing the obtained'Qusing adaptive binary arithmetic coding.

Step 6: Synonym substitution. ComparedQwith'S, synonym substitutions are performed to make the recovered synonyms whose encoded values equal to the corresponding bit values inQ. Finally, the cover text is exact recovered.

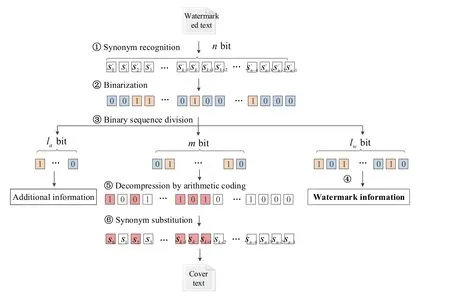
Figure 4: Watermark extraction and cover text recovery

5 Experimental results and analysis

In order to test the performance of the proposed method, we randomly downloaded 1000 texts from the Gutenberg corpus to conduct experiments. The carrier texts were divided into five sets. We try to guarantee the texts in the same set contain the same number of synonyms, which is an effort to make the objective evaluation of the proposed method.Thus, we cut off each cover text to contain appointed number of synonyms. A text in the five sets contains 200, 400, 600, 800, 1000 synonyms, respectively. The final cover text sets are denoted as cover200, cover400, cover600, cover800, and cover1000 respectively.

5.1 Reversibility analysis

Taking the first six chapters of the famous book “Wuthering Heights” downloaded from the websitehttp://en.eywedu.net/17/15/index.htmlas an example cover text, 493 synonyms are recognized. According to the synonym quantization rule in Definition 1,the 493 synonyms are quantized into a binary sequence shown in Fig. 5.

By performing adaptive binary arithmetic coding, the 493-bit binarized synonym sequence is compressed into 216 bits, which is shown in Fig. 6. As a result, a 277-bit redundant space, which can be used for accommodating the watermark information, is obtained from the original cover text.

“Wuthering Heights” was written by Emily Bronte in 1847. We use the information “Emily Bronte published in 1847” as a watermark information for protecting its copyright. The ASCII values of the characters in the watermark information are converted into a 210-bit binary sequence before being embedded into the example cover text. Here, only 7 bits is utilized to expressed a character. The binarized watermark information is shown in Fig. 7.

In order to distinguish the compressed synonym sequence and the binarized watermark from the extracted embedded information, additional information including their lengths are estimated. As the number of all synonyms in the example cover text is 493, 9 bits isemployed to record the length of the compressed synonym sequence, which is 216. We convert 216 into a 9-bit binary value is “011011000”. As the remaining space is 493-216-9=268, 9 bits is required to record the length of the watermark information, which is“011010010”. Thus, the complete embedded information is shown in Fig. 8.

Figure 5: The binarized synonym sequence in the example cover text

For the watermarked textT', we first count synonyms inT'. As there are 493 synonyms,at most 9 bits are required to record the length of the compressed synonym sequence in

Figure 7: The binarized watermark information

Figure 8: The complete embedded information

The complete embedded information including 444 bits information will be embedded into the example cover text by synonym substitution operations. In this process, the synonyms whose encoded values do not match the corresponding embedded bits are replaced by their synonymous words. The binarized synonym sequence in the watermarked text is shown in Fig. 9.

As the embedded information is shorter than the binarized synonym sequence, the last 49 synonyms are not employed to carry any information, whose corresponding encoded values are in italics in Fig. 9. And the values of the substituted synonyms are marked with bold emphasis.the cover textT. We read the first 9 bits of the binarized synonym sequenceS'inT',then we know the compressed synonym sequence inS'is 216 bits. And we can deduce that the length of the watermark information should not exceed 268, which is recorded by the next 9 bits “011010010” inS'. Therefore, the compressed synonym sequenceQ'can be obtained by reading the next 216 bits fromS', and the watermark information can be extracted by converting the next 210 bits fromS'into characters. Thus, the watermark“Emily Bronte published in 1847” is successfully extracted. The binarized original synonym sequence can be recovered by decompressingQ'with adaptive binary arithmetic coding. Compared the recovered synonym sequence with the synonyms inT',some synonyms are replaced by their synonymous words to recover the original synonyms. As a result, the recovered text employs the same synonyms with the cover text.Namely, the cover text is recovered without distortion.

Figure 9: The binarized synonym sequence in the watermarked text

In a word, our proposed method can not only extract the watermark successfully, but also recover the cover text reversibly. It is worth noting that only the watermarked text is required for the receiver. Any auxiliary data are not shared by sender and receiver for watermark extraction and cover text recovery. It improved the security of the proposed method compared with the existing similar reversible natural language watermarking methods, which always required to transmit securely a large number of auxiliary data.

5.2 Embedding capacity analysis

By the analysis of our proposed method, it can be found that the embedding capacity is determined by the compression capability of compressing the binarized synonym sequence in the cover text by adaptive binary arithmetic coding. We use the compression ratio to estimate the embedding capacity of the proposed method, which is defined by 1-compression ratioto measure the average bits embedded into each synonym.

The compression ratios of parts cover texts are shown in Fig. 10, which are randomly selected from the cover sets cover800 and cover1000. It can be seen that the synonyms used for embedding information can be effectively compressed by arithmetic coding.Thus, the compression will provide chance for synchronously embedding essential information to recover the cover text along with the watermark information. And it can provide a considerable embedding capacity.

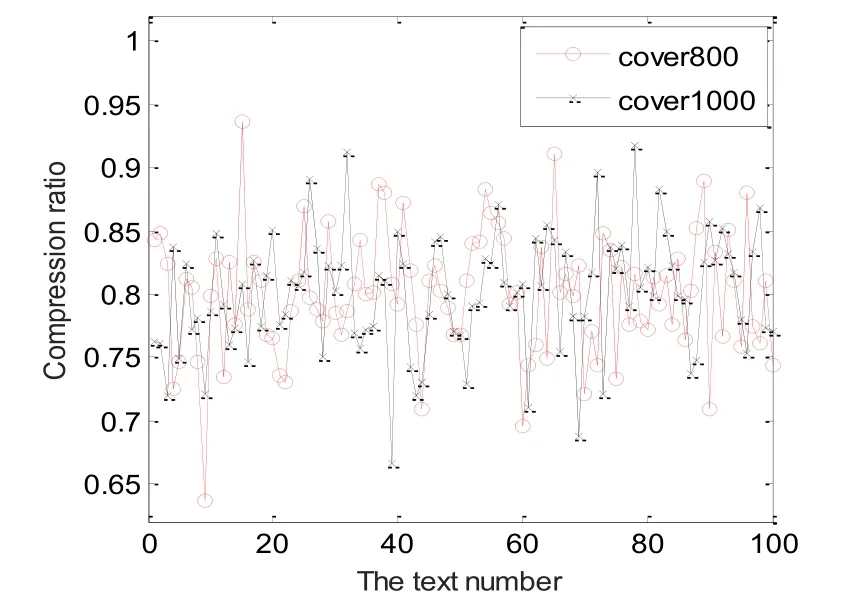
Figure 10: Parts of compression ratios

In order to given more details, we calculated the ratios of MFSs and compression ratios in all tested cover texts. Their distributions are shown in Fig. 11 and Fig. 12, respectively.Ratios of MFSs in cover texts are concentrated in the range of [0.7, 0.9]. Nearly 93.8% texts fall into this range. While the compression ratios are concentrated in the range of [0.7, 0.8],covering about 38.2% texts. The compression ratios of 26.9% texts are within range of [0.6,0.7]. We can see that our proposed method can obtain good compression performance by using arithmetic coding. As a result, the embedding capacity of the proposed method is excellent. Evenly, the embedding capacity of few texts can exceed 0.5.

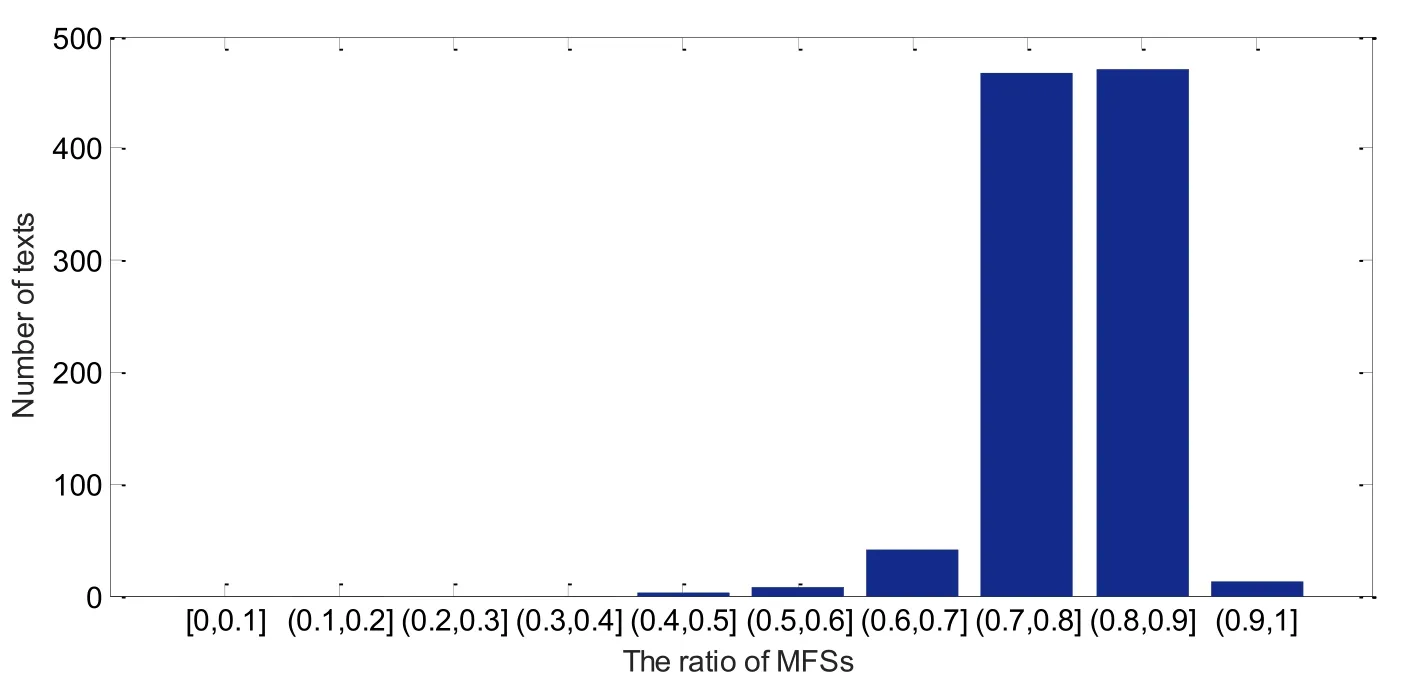
Figure 11: The distribution of the ratio of MFSs in cover texts

Figure 12: Compression ratio distribution in cover texts

More experimental results are analyzed in detail. We estimated the average ratios of MFSs, compression ratio and embedding capacity of each cover set. The results are listed in Tab. 1. We can see that our proposed method achieves a high average embedding capacity, which is over 0.2341 per synonym. Significantly, the embedding capacity increases with ratio of MFSs increasing, and with the compression ratio decreasing.Meanwhile, the larger the number of synonyms in a cover text is, the larger the embedding capacity is.

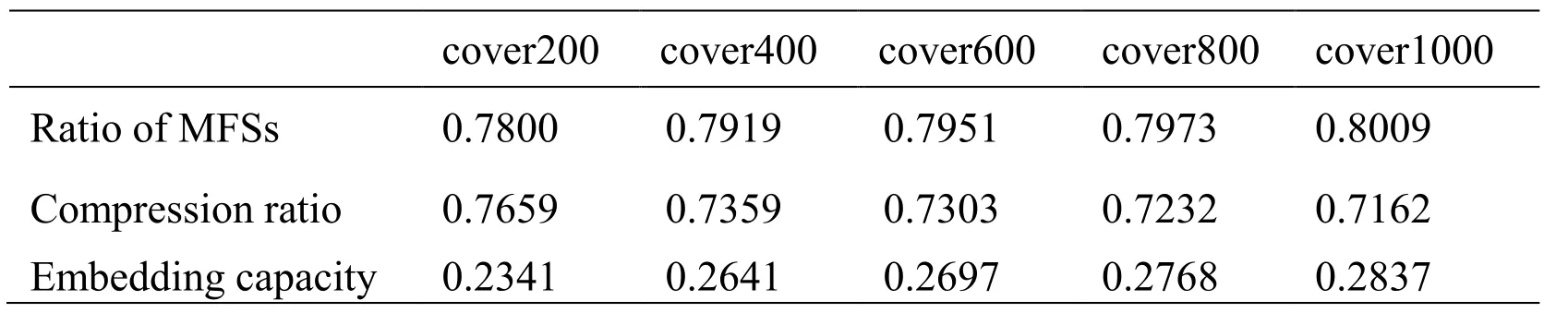
Table 1: The results of average embedding capacity

6 Conclusions

In this paper, we address the problem of losslessly recovering original cover text in the watermarking method. We present a reversible watermarking method by using synonym substitution and adaptive binary arithmetic coding. First, a suitable rule is designed to quantize synonyms in the cover text by analyzing the relative word frequency characteristics of synonyms. Adaptive binary arithmetic coding is selected to compressed the binarized synonym sequence for providing extra space to accommodate the watermark information. The compressed synonym sequence accompanied with the watermark information is embedded by synonym substitutions, which is employed for lossless and reversible recovery of original cover text for receivers. Experimental results show that the proposed method can not only extract watermark information successfully for protecting the copyright of the cover text, but also recover the original cover text reversibly. Additionally, the proposed method has a quite high watermark embedding capacity. As our ongoing work, we will continue to improve the embedding capacity.

Acknowledgments:This project is supported by National Natural Science Foundation of China (No. 61202439), partly supported by Scientific Research Foundation of Hunan Provincial Education Department of China (No. 16A008), and partly supported by Hunan Key Laboratory of Smart Roadway and Cooperative Vehicle-Infrastructure Systems (No.2017TP1016).