基于Fisher向量投影的支持向量机增量算法

吴　青, 赵　祥

(西安邮电大学 自动化学院, 陕西 西安 710121)

支持向量机(support vector machines, SVM)是一种基于统计学习理论的机器学习方法[1-2]，其借助最优化理论来解决机器学习问题，体现了统计学习理论中的结构风险最小化思想，目前已经得到了广泛的应用[3-5]。支持向量(support vectors, SV)是SVM训练样本中的一组特殊向量集合，这些向量通常离最优分类面较近，对最终的分类面的确定起着决定性的作用[6]。通常情况下，SV只占训练集的一部分，但是在标准SVM算法的学习过程中，大量时间花费在非SV的样本上，当处理大规模样本集时，算法的学习效率进一步降低，使得SVM算法在很多实际应用问题中受到制约[7]。因此，提高算法的效率是一个很重要的研究课题。

在支持向量机的基础上提出了增量学习SVM(incremental learning algorithm of SVM, ISVM)[8]算法。由于ISVM算法在处理大规模数据集以及流数据方面具有优势，已经得到了广泛的研究[9-10]。与标准SVM算法相比，其优势在于能够充分利用历史训练信息，无需对加入新增量后的训练集重新训练，但是其训练样本中包含了很多对最终结果无用的数据，对算法的训练效率造成了一定的影响。为了解决上述问题，一种基于向量投影的支持向量机增量学习算法[11]被提出，该算法利用预选取训练样本的方法对训练样本进行预处理，有效地提高了增量算法的训练速度，但其选取边界样本的方法过于简单，致使选取的边界样本的数目过多，影响了算法的性能[12]。

为了提高算法学习效率及其在处理大规模数据集和流数据方面的能力，本文拟利用基于向量投影的支持向量预选取方法[12]，将基于Fisher准则的边界向量预选取方法与增量算法相结合，提出一种基于Fisher判别向量投影的支持向量预选取增量算法(SVs pre-extracting method of ISVM based on vector projection of Fisher discriminant, FP-ISVM)，根据支持向量机中SV的几何分布特性对样本进行预处理，在不影响最终训练结果的前提下减少参与训练的样本数目，再结合增量算法，充分利用历史训练信息，减少重复训练的样本数目，压缩训练样本集的规模，提高算法的训练速度。

1　支持向量预选取

1.1　支持向量机

首先考虑线性可分的情况，假设一组训练样本D={(xi,yi)},i=1,2,…,l，其中，xi∈n表示第i个样本，yi∈{-1,1}表示样本所属类别。训练的最终目的是找到一个最优分类面，使得两类样本之间以最大间隔分开，使泛化误差达到最小或者有上界[13]。这个最优分类面即超平面。要找到这个超平面，就转变为求解一个线性约束的二次规划(quadratic programming, QP)问题。引入拉格朗日乘子α，最终转化为求解上述规划的对偶规划问题[14]。

对于非线性分类情况，可通过核函数(kernel function)K(xi,xj)=φ(xi)φ(xj)将训练样本从输入空间n映射到高维特征空间，并在高维特征空间中构造出最优分类超平面。

1.2　支持向量预选取方法

在求解上述二次规划的对偶问题时，系数αi对应每一个训练样本的解，在这些解中，存在许多系数αi=0，最优分类面的确定仅依赖于对应αi≠0的样本点，这些样本点被称为支持向量[2]。通常情况下支持向量只是训练样本的一部分，且正好位于两类边界上，如果可以通过对训练样本进行预处理，筛选出那些可能成为支持向量的边界向量，则可以有效地提高算法学习效率。

在现实应用中遇到的数据通常都是高维的，不能直观地确定数据边界。为了更好地确定边界向量集合，需要对原始数据降维处理，将原始样本投影到某一直线上，然后在一维空间确定边界向量集合。投影直线的确定，关系到边界向量预选取的效果，直接影响算法的性能，可以根据原始数据是否线性可分选择不同的投影直线确定方法。

1.2.1线性可分情况

采用Fisher判别法来确定线性可分情况下的最佳投影直线。根据Fisher准则的基本原理[15]，找到一个最佳投影方向，使两类样本在该方向上投影之间的距离尽可能远，即类间离散度最大，而每一类样本的投影之间尽可能紧凑，即类内离散度最小，从而使分类效果最佳。具体实现如下[15]。

设初始样本分别为

两类样本的中心分别为

计算各样本的类内离散度矩阵Sg和总类内离散度矩阵Sw:

再求出两类样本间的类间离散度矩阵

SB=(m1-m2)(m1-m2)T。

因为Fisher准则要解决的基本问题就是找到一个最佳投影方向w，使得两类样本在该方向上的投影能够尽可能的分开，以达到最好的分类效果。由Fisher准则的定义可知，要想获得最好的分类效果即要求两类样本间的类间离散度SB尽可能大，总类内离散度Sw尽可能小，为此，构造Fisher准则函数

其中，wT表示w的转置。通过求解maxJF(w)来得到最佳投影方向

1.2.2非线性可分情况

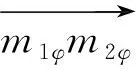
首先，定义特征空间中样本与2个样本中心之间的Euclidean距离，并将其求法以定理的形式给出。自中心距离指样本与本类样本中心向量之间的距离，互中心距离指样本与它类样本中心向量之间的距离，中心距离指两类样本中心之间的距离。

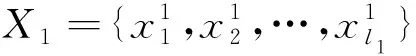
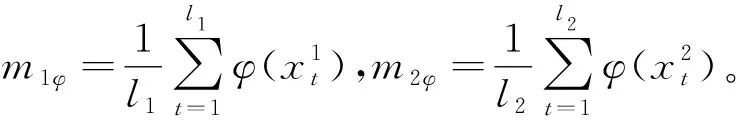
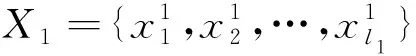
互中心距离分别为

2　基于Fisher向量投影的SVM增量学习算法

2.1　边界向量集合的确定

2.1.1线性可分情况

已知两类模式的初始训练样本分别为

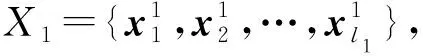
线性可分情况下确定边界向量集合方法的具体实现步骤如下。

步骤1利用Fisher判别法找到最佳投影直线方向w，确定最佳投影直线；

步骤3构造边界向量集合。若初始训练样本X=X1∪X2={x1,x2,…,xl}中对应投影点与中点c0之间距离分别满足不等式

2.1.2非线性可分情况

对非线性可分情况，通过φ(·)将原始样本映射到高维特征空间，选取两类样本在高维特征空间中的样本中心所在直线为最佳投影直线，将原始样本投影到该最佳投影直线上，再根据上述定义的特征空间中样本及样本中心之间的相关距离筛选出所需的边界向量。原始样本在特征空间中的投影示意图，如图1所示。

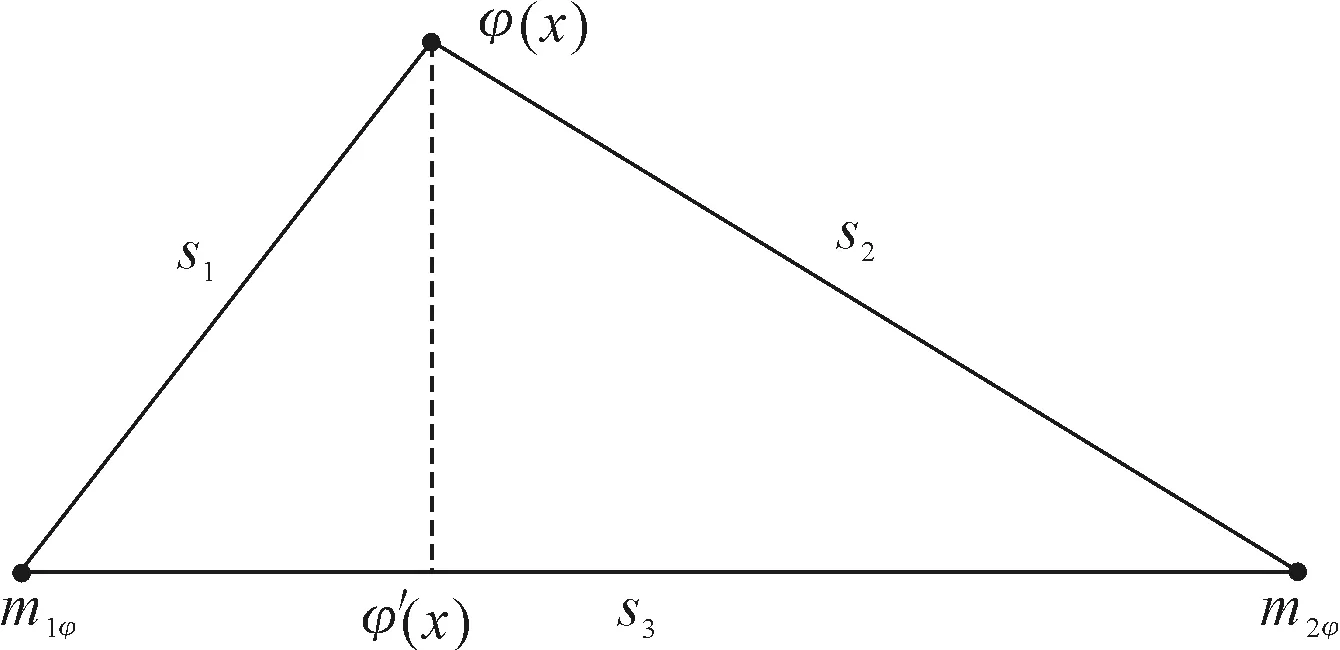
图1　原始样本在特征空间中的投影

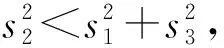
对第一类中投影点位于m1φ和m2φ之间的样本，分别求出它们的投影点到m1φ的最大距离D1和最小距离D2，边界向量确定规则如下。

(1) 若D1≤D2，则从投影点位于m1φ和m2φ之间的样本中，选出投影点到m1φ的距离d满足不等式

或者

的样本作为边界向量，其中0≤λ≤1。

(2) 若D1>D2，则分别从投影点位于m1φ和m2φ之间的两类样本中，选出投影点到m1φ的距离d满足不等式

或者

的样本作为边界向量，其中0≤λ≤1。

2.2　算法步骤

设初始样本集为X0，增量训练样本集为X1，并且设X0∩X1=∅。基于Fisher向量投影的SVM增量算法FP-ISVM的具体步骤如下。

步骤1对初始样本集X0进行预处理，得到边界向量集T0，在T0上训练得到分类器M0和支持向量集V0；

步骤2新增样本X1，对这批样本进行预处理得到相应的边界向量集T1，在T1上训练得到新的分类器M1和支持向量集V1；

步骤5重复步骤2、3、4，即可完成对多批增量样本的处理。

3　实验结果及分析

下面对所提出的FP-ISVM算法进行数值实验。文中的算法均使用MATLAB R2012b软件的编程语言实现，操作系统为Windows10 64位，实现的硬件条件是Intel Core i7-4790，主频3.6 GHz，计算机的内存是8 GB，实验中的算法均采用高斯核函数，距离均为欧式距离。

3.1　对NDC数据集的实验

实验数据来自NDC(normally distributed clustered)数据集。实验中，训练样本的总个数为12 000个，把训练样本分为4个部分，分别为初始训练样本，增量1，增量2，增量3，对应的样本个数分别为4 800、3 600、2 160、1 440，测试样本的个数为2 400。3种算法处理NDC数据集的实验结果比较，见表1。

表1　三种算法对NDC数据集的实验结果比较

如表1所示，在处理NDC数据集时，FP-ISVM算法与标准SVM相比训练时间缩短了94.41%，与文献[11]中的算法相比训练时间缩短了64.26%。通过对样本的预处理，FP-ISVM算法减少了参与训练的样本数目，在数据逐批增加的过程中，利用历史数据信息，避免对所有样本的重复训练，提高了算法的学习效率。由于在数据预处理和增量学习的过程中可能会去掉少量的有效数据，所以导致精度略微下降。

3.2　对UCI数据集的实验

试验对来自标准UCI((university of California Irvine))数据库的musk数据集进行实验。该数据集共6 598个样本，样本维数166，将该数据集分成2组，一组为测试样本集，共包含659个数据；另一组为训练样本集，共包含5 939个数据，从中随机选取2 375个数据作为初始训练样本集，并将剩余的数据随机分成3组，构成3个增量训练样本集，样本个数分别为1 782、1 069、713。数值实验结果如表2所示。

从表2可以看出，在实际数据集上，FP-ISVM算法通过对数据的预处理和增量学习算法，可以有效地压缩训练样本的规模，在精度略有降低的情况下训练时间大幅度地缩短，提高了训练速度，而且随着训练样本数目的逐渐增加，这种优势更加明显。算法FP-ISVM所需时间与标准SVM相比减少了86.67%，与文献[11]中的算法相比训练时间减少了33.12%，进一步体现了该算法在处理大规模数据集以及流数据方面的优势。

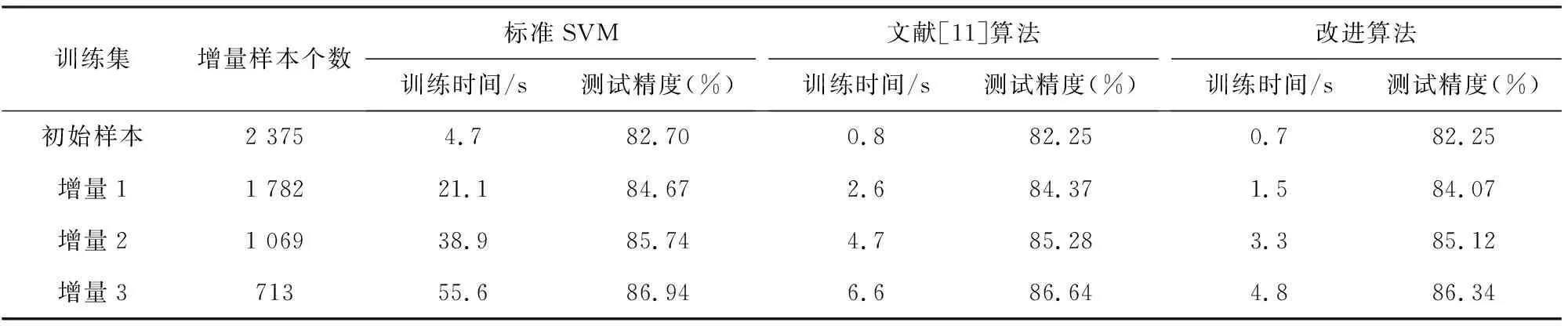
表2　三种算法对UCI数据集的实验结果比较

4　结语

为了提高支持向量机在处理流数据及大规模数据集时的学习效率，提出一种新的基于Fisher判别的支持向量预选取增量算法。该算法根据支持向量机中支持向量的分布特性对初始训练集及增量集进行预处理，结合增量算法，充分利用历史数据信息，减少对样本的重复训练，压缩参加训练的数据规模，提高训练速度。但是由于在数据预处理和增量学习的过程中可能会将一些有效数据剔除，导致精度略微有点下降。实验结果表明，这种算法在速度上优于标准支持向量机算法及文献[11]中的算法，能够提高支持向量机的学习效率，适合于样本集规模较大的情况；另一方面，在训练样本逐渐增加的情况下，该算法基于之前训练的结果对后继增量进行学习，提高了处理流数据的能力。