基于FABEMD的纹理图像分类算法

胡明娣, 臧艺迪, 徐家慧

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

纹理是图像的一种基本特征。纹理分类作为纹理分析的一个重要研究领域，受到广泛地关注[1]，其在细胞图像识别、卫星图像分类、指纹识别等领域得到了越来越多的应用[2]。

对纹理特征的描述是纹理图像进行分类首先需要解决的问题[3]。统计法虽然容易实现纹理特征的描述，但图像大量的统计特性，使得计算量较大[4]。模型法可以产生实用的纹理特征，但计算量大限制了其应用领域[5]。二维经验模式(bidimensional empirical mode decomposition, BEMD)方法[6]是针对非线性、非平稳性二维信号的一种自适应处理算法，广泛应用在纹理图像检索领域，但在纹理图像曲面插值操作中的高时间复杂度限制了它的应用。文献[7]将灰度共生矩阵(gray lever co-occurrence matrix, GLCM)结合BEMD方法对纹理图像进行分类，但未考虑到时间复杂度；文献[8]将BEMD与局部二值模式结合提取纹理图像的特征参数，并使用支持向量机进行分类，精确度较高，但是算法复杂度高。文献[9]针对BEMD的分解过程需要大量的时间冗余提出了一种简单高效的快速自适应二维经验模式分解方法(fast and adaptive bidimensional empirical mode decomposition, FABEMD)，但未应用到纹理图像分类中。

在文献[7]和文献[9]的研究基础上，本文拟提出一种基于FABEMD的纹理图像分类算法。该算法首先利用FABEMD算法将原始纹理图像分解成3个二维固有模态函数(bidimensional intrinsic mode functions, BIMF)以及余量的和；然后使用灰度共生矩阵提取每层BIMF分量不同尺度的纹理特征参数，组成特征向量；最后，采用最小距离分类器(minimum distance classifier, MDC)进行纹理图像的分类。

1　基于BEMD的纹理图像分类

1.1　利用BEMD方法分解图像

二维经验模式分解广泛应用于图像处理领域，其基本思想是把信号分解成一些由高频到低频的内在模式函数和余量图像[10]。

BEMD分解实现过程如下[11]。

(1)原始图像初始化，求取局部极值点(极大值点和极小值点)；

(2)分别对局部极大值点和局部极小值点进行曲面插值，得到上包络面和下包络面，进而计算均值包络面；

(3)计算原始图像与均值包络面的差值得到模态函数；

(4)给定终止条件。

重复步骤(1)到步骤(3)，直到满足给定的终止条件得到第一个模态函数，用原始图像减去第一个模态函数得到的第一个余量，对残余分量重复步骤(1)到步骤(4)，依次得到图像的N个固有模态函数和第N个残余。

1.2　使用灰度共生矩阵提取纹理参数

在纹理图像分类中，常使用灰度共生矩阵来分析灰度的空间相关性[12]。灰度共生矩阵是通过统计图像上保持一定间距且分别具有灰度特征的2个像素得到的，定义为图像中间距为d的2个像素同时出现的联合概率分布。

用p(x,y)表示灰度图像中的任一像素点且其灰度值为f(p)=w,w∈{0,1,…,W-1}。假设p1(x1,y1)和p2(x2,y2)为灰度图像中2个像素点，它们之间的距离为d且灰度值分别为f(p1)=w1，f(p2)=w2，pc为像素值(w1,w2)同时出现的概率，则可定义共生矩阵

Cd,θ(w1,w2)=pc{f(p1)=w1∧f(p2)=w2:
|p1-p2|=d}。

其中，θ∈{0,45°,90°,135°}，d取1。基于上述灰度共生矩阵的定义，常用的特征统计量共14个，目前最常用的纹理特征参数主要有能量、熵、对比度和相关性[13]。

1.3　最小距离分类器进行分类

最小距离分类器，属于统计识别方法，是分类器中最常用的一类分类方法，又称最近邻分类[14]，它是通过求解出未知类别向量到事先已知的各类别中心向量的距离，然后将待分类的向量归结为这些距离中最小的那一类。

其基本过程为：假设c个类别代表模式的特征向量用R1,R2,…,Rc表示，x是被识别模式的特征向量，|x-Ri|是x与Ri(i=1,2,…,c)之间的距离，如果|x-Ri|最小，则把x分为第i类。最小距离分类器因计算简单、分类速度快，常被应用于实时性要求高的系统中[15]。

2　基于FABEMD的纹理图像分类

在求解覆盖图像的上下包络面时，BEMD采取曲面插值的方法，使算法复杂度较高。针对这个缺点，本文采用FABEMD方法，它与BEMD的主要不同之处是求解图像的上下包络面时，BEMD使用的是曲面插值操作，而FABEMD使用的是统计滤波和平滑滤波操作，使得算法的迭代次数减少[16]。图像经过FABEMD分解之后，得到n个二维固有模态函数，分别记为B1,B2,…,Bn，它们在频率上由高到低、尺度上由细到粗，其中频率最低、尺度最粗的叫作余量，将所有固有模态函数和余项线性叠加即可恢复原始图像。

运用FABEMD对选定的图像进行分解，然后使用GLCM提取各BIMF分量的纹理特征参数，组成特征向量，最后运用MDC进行分类。

2.1　运用FABEMD算法分解图像

设I(m,n)是一幅图像，运用FABEMD算法分解图像步骤如下。

步骤1原始图像初始化，当i=1时，令

Ri(m,n)=I(m,n)。

步骤2用8-邻域法分别算出Ri(m,n)的局部极小值点Pmin(m,n)和局部极大值点Pmax(m,n)。此处的极大值点必须严格大于周围的点，极小值点必须严格小于周围的点。

步骤3计算每层局部极值图中极值点相互之间的欧氏距离，得到MAX/MIN统计滤波器的窗口。

要确定滤波器窗口的大小，需要计算出每一层局部极值图中极大值与其他极大值的欧氏距离，将最接近的欧氏距离存储在da,max向量中，同理，计算每一层局部极值图中极小值与其他极小值的欧氏距离，将最接近的欧氏距离存储在da,min向量中，计算滤波器窗口的大小。原理如下。

We,1=min{min{da,max},min{da,min}},

(1)

We,2=min{max{da,max},max{da,min}},

(2)

We,3=max{min{da,max},min{da,min}},

(3)

We,4=max{max{da,max},max{da,min}}。

(4)

为了便于筛选以上操作，将上述4个值约等于最接近的整数，步骤如下。

(1) 将式(1)—式(4)中计算所得的滤波器窗口大小的值记为We,j(j=1,2,3,4)；

(3) 分别计算

并比较两值大小；

把顺序统计滤波器的宽度We,1、We,2、We,3、We,4使用上述方法取整后，分别记为类型1，类型2，类型3，类型4。很明显，类型We,1的窗口值最小，类型We,4窗口值最大。顺序滤波器的不同的窗口大小适用于不同的应用目的，这个特征被称为FABEMD算法的自适应性。

步骤4通过对Ri(m,n)使用MAX/MIN统计滤波器来构造极大值包络和极小值包络。令一层的平滑窗口大小为We,j，对局部极值图进行平滑滤波。通过滤波后得到极大值包络Emax-s(m,n)和极小值包络Emin-s(m,n)；

步骤5计算Emax-s(m,n)和Emin-s(m,n)的均值包络

步骤6求解第i个二维固有模态函数

Bi(m,n)=Ri(m,n)-Em(m,n)；

步骤7计算余量

Ri+1(m,n)=Ri(m,n)-Bi(m,n)；

步骤8判别分解层数是否满足3层，或者判别图像余量Ri+1(m,n)中是否少于3个极值点。如果满足以上任意一个条件，那么余量为

C(x,y)=Ri+1(m,n)，

至此分解完成。否则，回到步骤2，继续获得下一个二维固态函数。

2.2　提取相关纹理特征参数

针对2.1节中所得的3层BIMF分量，采用GLCM对这3层BIMF分别提取能量，熵，对比度，相关性4个纹理特征参数，其中B1分量的特征向量记为F1=[f11,f12,f13,f14]，B2分量的特征向量记为F2=[f21,f22,f23,f24]，B3分量的特征向量记为F3=[f31,f32,f33,f34]，将F1,F2,F3组成一个扩展的12维特征向量F=[F1,F2,F3]。

2.3　采用MDC进行分类

针对2.2节中得到的特征向量，采用MDC方法进行分类。FABEMD算法总流程图如图1所示。

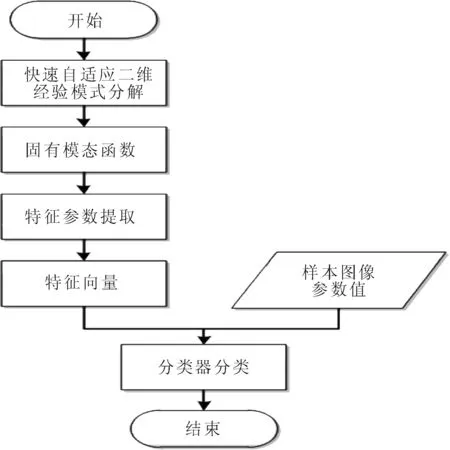
图1　FABEMD算法流程图

3　实验及结果分析

在相同的实验环境下，与文献[7]所用的方法进行对比实验。

3.1　实验条件及过程

实验所用机器的CPU是Intel四核处理器i5，内存4 G，操作系统是64位的Windows10，算法用Matlab实现。选取Brodatz纹理库中的10类纹理图像，大小为640×640，灰度级为256，如图2所示。

每类图像随机截取40幅160×160大小的图像，其中，第1—10幅图用以训练产生模式类的样本均值，第11—30幅用以分类识别。采用FABEMD对这40幅图像进行分解，每幅图像分解为3层BIMF和1个余量，使用GLCM提取每层BIMF的4个纹理特征参数，构成特征向量，最后通过MDC进行分类。

图2　Brodatz纹理库中10类图像

3.2　实验结果分析

采用上述FABEMD算法对一幅纹理图像(Brodatz纹理库中的D64，大小为640×640)进行分解，分解结果如图3所示。

图3　D64的FABEMD分解结果

如图3所示，图像D64经过FABEMD分解得到的B1、B2、B33个分量和余量，B1到B3反应原始图像各个尺度的详细信息，可以看出B1反映了图像的主要信息，而余量反应了图像的趋势信息。

对上述纹理图像D64分解得到的B1、B2、B33个分量分别提取4个方向上的4个纹理特征参数，将每个特征4个方向的特征参数值作算数平均，得出最终纹理参数向量，结果如表1—表3所示。

由表1可得，D64的B1分量的纹理参数均值分别为0.053 1, 4.990 9, 2.389 3, 0.505 6。

由表2可得，D64的B2分量的纹理参数均值分别为0.051 1, 4.977 9, 1.1998, 0.849 5。

由表3可得，D64的B3分量的纹理参数均值分别为0.066 2, 4.497 6, 0.549 2, 0.929 9。

由上可得图像D64的纹理参数特征向量为

[0.053 1, 4.990 9, 2.389 3, 0.505 6,0.051 1, 4.977 9, 1.1998, 0.849 5,0.066 2, 4.497 6, 0.549 2, 0.929 9]。

表2　D64的B2分量的纹理参数值

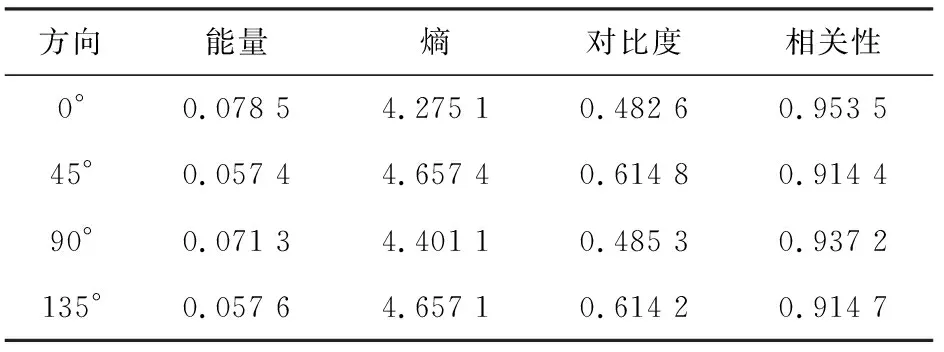
表3　D64的B3分量的纹理参数值

本文算法与文献[7]中BEMD算法分别进行纹理图像分解所需的时间对比，如图4所示。

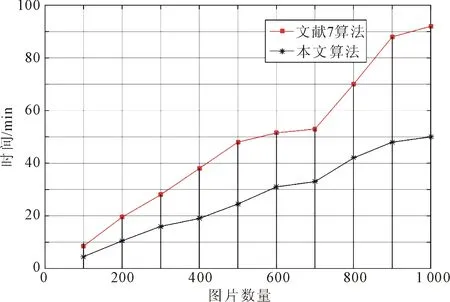
图4　算法分解图像时间对比

从图4可以看出，所采用的FABEMD相对于文献[7]的BEMD分解算法，在相同图片数量的情况下缩短了运行时间，且随着图片数量的增加，差距更加明显。选取Brodatz纹理图像库中具有代表性的10类样本图像进行实验，本文算法与文献[7]中BEMD算法分别进行纹理图像分解的平均分类准确率，如表4所示。

由表4可以看出，FABEMD算法的平均分类正确率(仿真中被正确分类的图像个数与参与分类的总图像个数的比值)达到86.28%，高于文献[7]算法的81.67%。

表4　MDC进行分类实验仿真结果

4　结语

针对BEMD算法应用于纹理图像分类时，其所使用的插值方法求包络时间长，准确率低的缺点，采用FABEMD算法，用滤波代替插值操作，首先使用FABEMD算法将纹理图像分解成3个BIMF和1个余量之和；然后使用灰度共生矩阵提取各BIMF的能量、熵、对比度和相关性这4个纹理特征参数，组成特征向量，最后运用最小距离分类器进行纹理图像分类。选取Brodatz纹理库中纹理图像进行仿真实验，实验结果表明，与文献[7]的BEMD分类方法进行相比，所提算法不仅缩短了运行时间而且平均分类准确率达到86.28%，表明了FABEMD在纹理图像分类时优于BEMD。