基于指数变换时频图增强的FSK信号特征提取

郑文秀, 覃艳琴, 常　虹

(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)

通信信号调制特征提取是通信对抗和电子侦察等领域的重要研究课题。其目的是在多信号环境和有噪声的条件下，通过提取信号的特征，将信号区分开来，从而为信号后续分析处理提供依据。

目前，对频移键控(frequency-shift keying，FSK)信号的特征提取主要从频谱特性等方面进行研究[1]。文献[2]从同类2FSK混合信号中提取微弱信号，该方法与2FSK信号的相关性有关，当信号相关时会有一定的失真，不相关时分类识别效果比较好。基于特征提取的调制识别方法，较好地解决了以往数字、模拟调制不能较好联合识别的问题，但获取特征参数过于复杂[3]。基于瞬时频率细微特征分析的FSK信号个体识别方法，解决了频率在短时间内变化规律不明显的特点，但如果噪声太大，信号的细微特征很有可能被噪声干扰[4]。平滑伪Wigner-Ville分布算法基本上抑制了提取FSK信号特征时存在的相干项。但在低信噪比条件下，提取的特征参数的准确率受到一定的限制[5]。低信噪比条件下FSK信号调制特征提取方法，提高了提取信号特征的准确率，但在信号时频分析时可能会产生频率的一些重叠现象[6]。

为了能够区分信号的载波频率，本文拟提出基于指数变换时频图像增强的FSK信号二维特征提取算法。该算法是在时频分析的基础上结合了图像处理技术，首先对FSK信号做离短时散傅里叶变换(discrete short time Fourier transform，DSTFT)[7]得到时频图；其次对时频图进行灰度转化和增强处理，得出灰度值矩阵，以灰度值矩阵的统计特征角二阶矩(angular second moment, ASM)能量作为特征提取参数，得ASM能量曲线；最后根据ASM能量曲线确定FSK信号有几条时频谱线以及谱线的位置，进而估计出不同谱线位置所对应的载波频率，从而区分出FSK信号的载波频率。

1　FSK信号离散短时傅里叶变换

FSK信号在信道传送时会受到噪声的影响。设接收机在时刻t的输入信号函数[8]

s(t)=x(t)+y(t)

(1)

(2)

ωn=2πfn,ωn∈{ω1,ω2,…,ωN}。

(3)

其中，x(t)表示时刻t的FSK信号。A为信号幅度；ωn为角频率，n表示载波频率个数，取值范围从1到N；fn为频率；θn为初相位；g(t)为时刻t的矩形信号，Ts为码元宽度。y(t)表示时刻t的高斯白噪声。

因接收机有带宽，高斯白噪声y(t)通过接收机后会变成高斯有色噪声y1(t)。假设采样频率是fs，则在时刻i的输出信号序列函数

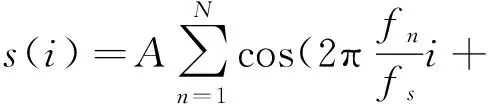
(4)

离散短时傅里叶变换(discrete short time Fourier transform，DSTFT)会将输入信号转换到离散化的时频平面上[9]。以时间和频率作为采样周期，则对于序列信号s(i)在时间点i和频率点k处的离散短时傅里叶变换为

(5)

其中，w(·)是窗函数，其窗口长度为M；j是虚数单位，m为序列信号点数，取值范围为0到M-1。

由式(5)可见，DSTFT实际上为加窗的离散傅里叶变换(discrete Fourier transform，DFT)，S(i,k)相当于取s(i)的有限长度序列进行DFT，因此,信号s(i)在时刻i的短时功率谱等于短时傅里叶变换的模平方，则短时功率谱为

p(i,k)=|S(i,k)|2。

(6)

根据s(i)在不同时刻i处的短时功率谱组成的短时功率谱矩阵为P(i,k)。其中，i和k的取值范围都为0到M-1，然后由短时功率谱矩阵可得时频图。

2　FSK信号的二维特征提取

2.1　时频图到灰度图的转化

信号的短时频谱图可采用灰度图来显示，因为灰度的深浅可表示频谱强度，平面上的横轴和纵轴可分别表示时间和频率[10]。

信号s(i)经过离散短时变换后，得短时功率谱矩阵P(i,k)，然后可得时频图。要把时频图转化为时频二维灰度图，需要把短时功率谱矩阵转化成灰度值矩阵。因灰度图像的灰度值取值为0—255的整数，而短时功率谱矩阵P(i,k)的值不都在0—255内，也不都是整数，因此先要把数值变换到0—255内[11]。既对矩阵P(i,k)的每个元素都除以矩阵P(i,k)中的最大元素，然后乘以255，再进行取整运算，以保证结果为0—255的整数，则取整运算后得灰度值矩阵为H(i,k)，然后根据灰度值矩阵就可得时频二维灰度图。

2.2　基于指数变换的时频二维灰度图增强

图像增强指数变换法的基本形式为[12]

Iout=c(Iin+εI)γ。

(7)

其中，Iin为原始图像数据矩阵；Iout为指数变换后的图像数据矩阵；c和γ为转换系数；为避免底数为0的情况，增加偏移量矩阵εI，ε为偏移量，I为单位阵。图像增强的效果与γ值有关。当γ=1时，相当于正比变换。当0<γ<1时，会将原始图像的灰度向高亮度部分映射。当γ>1时，会将原始图像的灰度向低亮度部分映射[13]。

因噪声的影响，时频二维灰度图分辨率较低，为了提高图像的分辨率，进行指数变换的图像增强处理，则时频二维灰度图增强后的灰度值矩阵为

G(i,k)=c[H(i,k)+εI(i,k)]γ。

(8)

再根据增强后的灰度值矩阵，得到增强的时频二维灰度图。

2.3　特征提取的实现步骤

特征提取是以时频二维灰度图的灰度值矩阵为依据，ASM能量是灰度值矩阵的统计特征，短时功率谱又包含了短时能量信息。因此短时功率谱可看作为ASM的局部能量，且载波处的ASM能量较大，则根据这些特性来进行特征提取，其特征提取流程如图1所示。

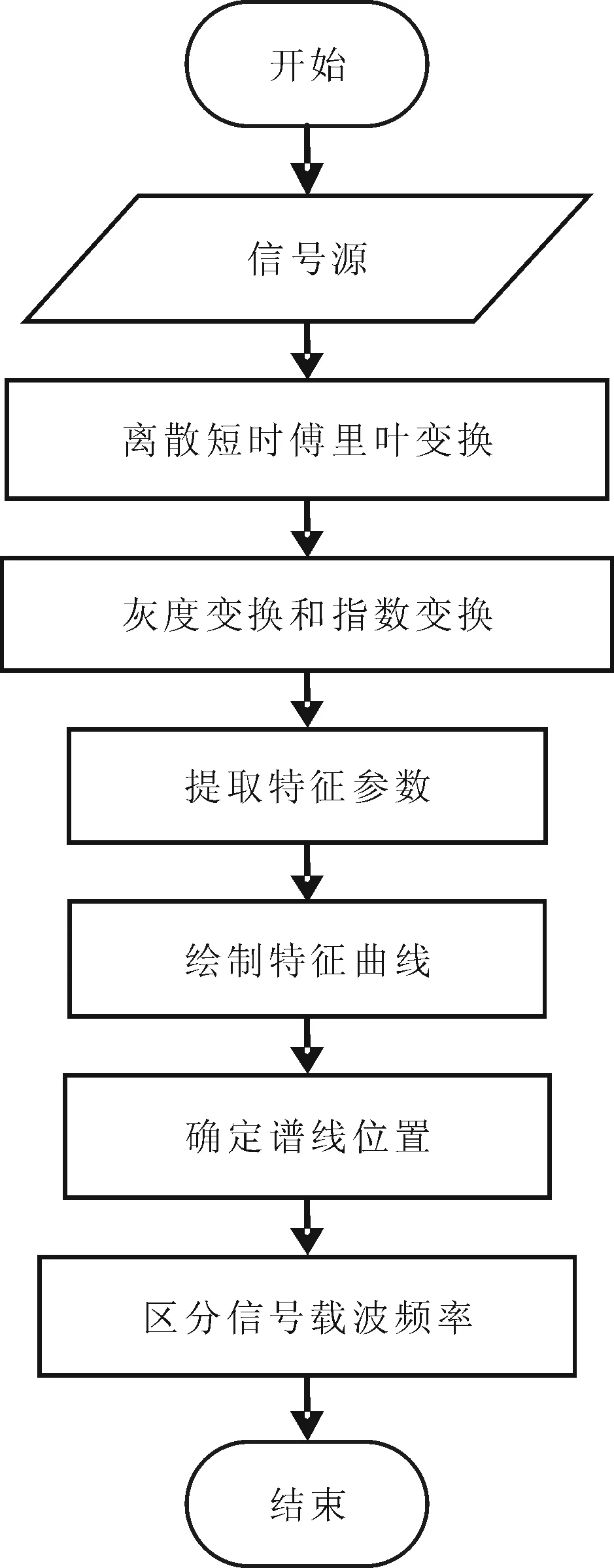
图1　特征提取流程

具体实现步骤可描述如下。

步骤1对FSK信号做离散短时傅里叶变换，得到时频图。对时频图做灰度处理，并进行指数变换，得到增强后的时频二维灰度图。

步骤2对增强的时频二维灰度图做数据提取，得灰度值矩阵G(i,k)。由灰度值矩阵G(i,k)的统计特征ASM能量[14]，可定义第m行的ASM能量

(9)

根据xm可知ASM能量向量为

X=(x0,x1,…,xM-1)。

(10)

步骤3分别以灰度值矩阵G(i,k)的行元素为横坐标，以ASM能量向量X中的元素为纵坐标，可得ASM能量曲线。根据曲线的极大值波峰，若曲线中有L个波峰，则可说明有L条谱线。根据向量X提取出L个波峰点的ASM能量值，也就是ASM能量较大值，再对应灰度值矩阵可知这L个值是矩阵G(i,k)中哪些L行的ASM能量值，则这L个行位置就是L条谱线的对应位置，因此谱线位置向量为

D=(d0,d1,…,dL-1)。

(11)

步骤4根据谱线位置，找出对应这L个位置的频率值，则这L个值就是信号载波频率的估计值，因此载波频率估计值向量为

F=(f0,f1,…,fL-1)。

(12)

步骤5根据以上各式可知FSK信号的时频图有多少条频谱线，并可确定谱线位置所对应的载波频率，从而区分出FSK信号载波频率数。

3　仿真及结果分析

为了验证方法的有效性，利用Matlab软件进行实验仿真验证。设定码元个数为1 000，载波频率分别为f1=3 MHz和f2=3.5 MHz，码速率为300 bit/s，采样频率为11.7 MHz的2FSK信号进行特征提取。

3.1　特征提取仿真实验

仿真实验以2FSK信号为例，将2FSK信号加入带宽为1.2 MHz的高斯白噪声，以信噪比10 dB和30 dB为例，仿真产生信号源。进行DSTFT变换，窗函数为汉明窗，窗口长度为100个采样点，指数变换的转换系数c=1，γ=0.8。在这两种信噪比下，2FSK信号的DSTFT变换时频图和时频二维灰度图的指数变换前后图以及ASM能量曲线的仿真结果都如下所示。

(1) 信噪比为10 dB的特征提取

信噪比为10 dB的时频图和指数变换前后的时频二维灰度图及ASM能量曲线，如图2所示。

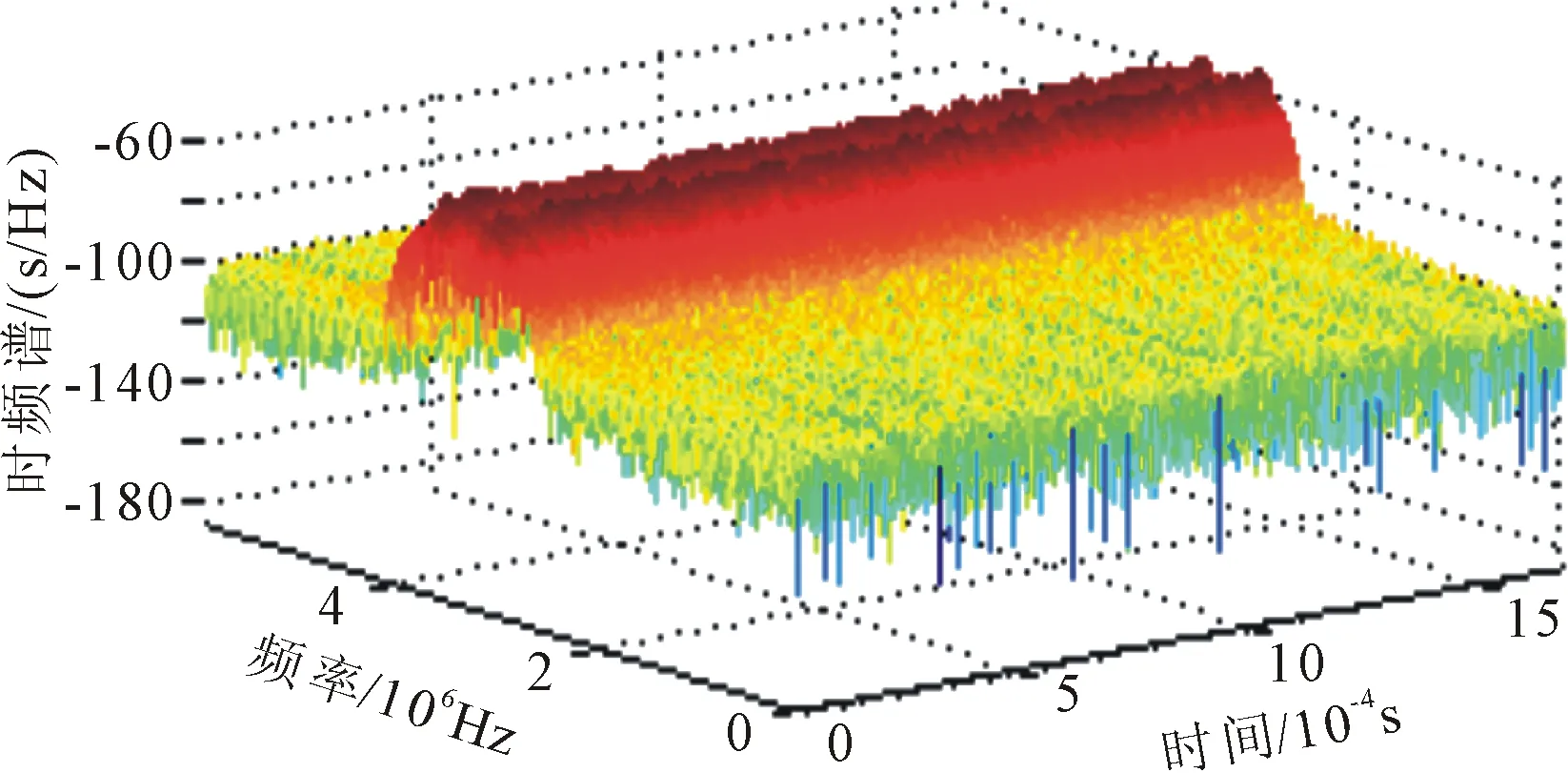
图2　10 dB下的2FSK信号的时频

图2是2FSK信号在信噪比为10 dB时，经过DSTFT变换得到的时频图，可以看到明显的两个峰值曲面。

根据时频图，进行灰度转换及指数变换的图像增强，在指数变换中，经过多次实验，结果表明当γ取0.8时，图像增强的效果较为理想。10 dB下的2FSK信号的时频二维灰度图，如图3所示。增强后的时频二维灰度图，如图4所示。

图3　10 dB下的2FSK信号的时频二维灰度图

图4　10 dB下增强后的时频二维灰度图

对比图3和图4可见，图像增强效果较为明显，噪声信号基本被去除，降低了噪声的影响，较好地保留了信号信息，提高了时频二维灰度图的分辨率。

根据时频二维灰度图的灰度值矩阵，得到10 dB下2FSK信号的ASM能量值曲线，如图5所示。

图5　10 dB下2FSK信号的ASM能量值曲线

由图5可知，ASM能量曲线有2个很明显的波峰，其ASM能量的2个较大值在60 MHz和80 MHz左右。对应的谱线位置在第130行和第150行附近，从而验证了2FSK有2个载波频率。

(2) 信噪比为30 dB的特征提取

30 dB下2FSK信号的时频图，如图6所示。

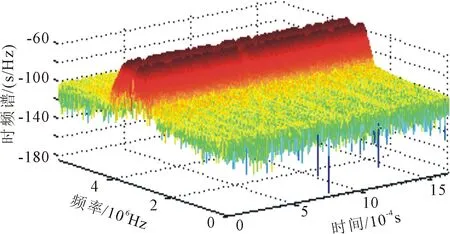
图6　30 dB下2FSK信号的时频图

从图6可以看出，时频图相比10 dB下的更加平滑。

再根据时频图，进行灰度转换及图像增强，指数变换转换系数值保持不变。则30 dB下的2FSK信号的时频二维灰度图，如图7所示。增强后的时频二维灰度图，如图8所示。

图7　30 dB下2FSK信号的时频二维灰度图

图8　30 dB下增强后的时频二维灰度图

通过图7和图8对比表明，噪声信号基本被抑制，信号信息大部分被保留，图像的分辨率提高，图片质量得到改善。再根据灰度图的灰度值矩阵提取出ASM能量值，并得到30 dB下2FSK信号的ASM能量曲线，如图9所示。

从图9可知，ASM能量曲线有2个很明显的波峰，从而知道对应的谱线位置也有2个，与之前的实验一样验证了2FSK有2个载波频率。

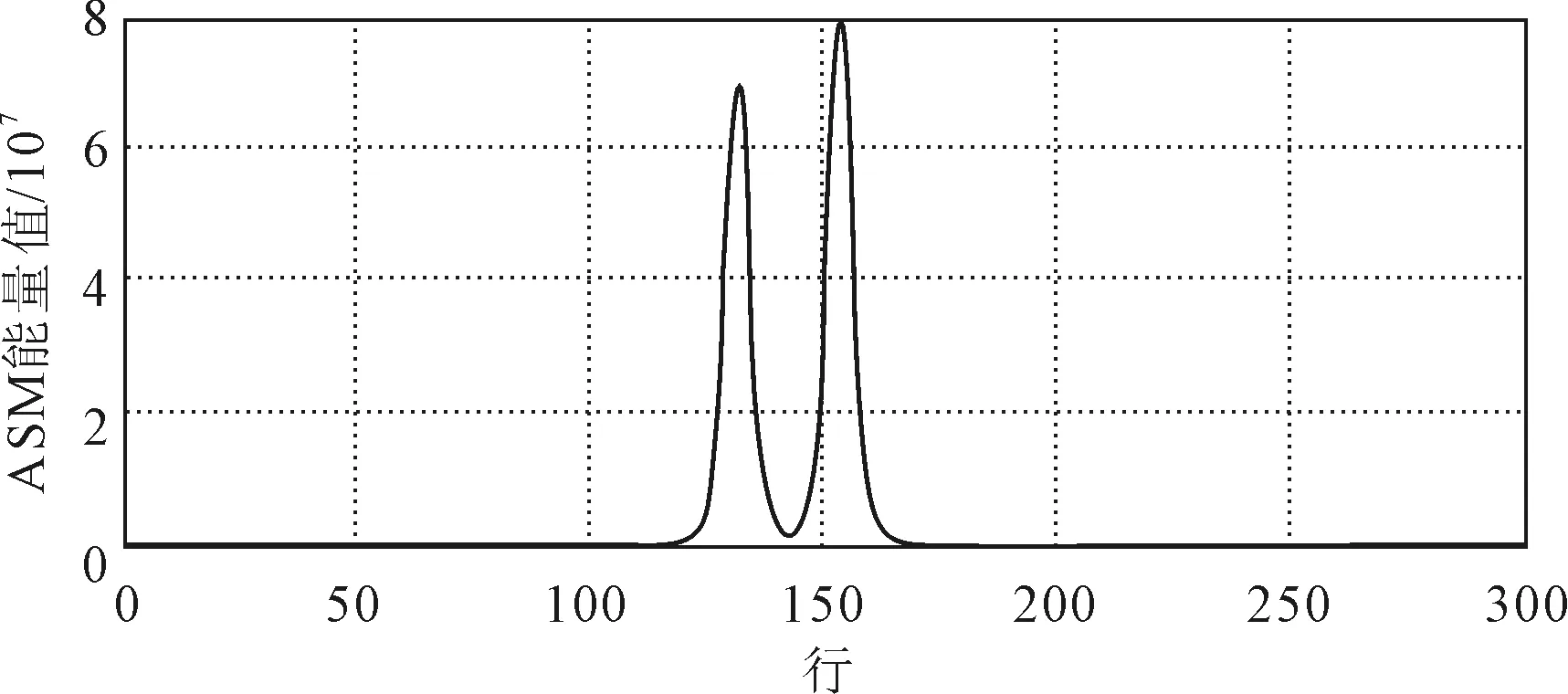
图9　30dB下2FSK信号的ASM能量曲线

信噪比分别为10 dB和30 dB下的实验结果，如表1所示。

表1　两种不同信噪比下的参数

根据表1可知，频率f1=3 MHz对应的谱线位置在灰度值矩阵的第132行，f2=3.5 MHz对应的谱线位置在灰度值矩阵的第154行，从表中可看出载波频率估计值与载波频率理论值存在一定的误差，但信噪比由10 dB变为30 dB时，误差减少，从而验证了算法的有效性和可行性。

3.2　不同信噪比下信号载波频率的性能试验

为了验证在各种信噪比条件下算法的稳定性，选取2FSK信号载波频率f1=3 MHz，信噪比从10 dB到30 dB，以2 dB为步进，在每个信噪比上进行500次蒙特卡洛实验，得到每个信噪比下的该载波频率估计值的统计数据，根据统计数据计算出每个信噪比下的该载波频率估计值的均值，即最终的载波频率估计值，然后计算出该载波频率估计值与理论值的相对误差。不同信噪比下信号载波频率的相对误差，如表2所示。

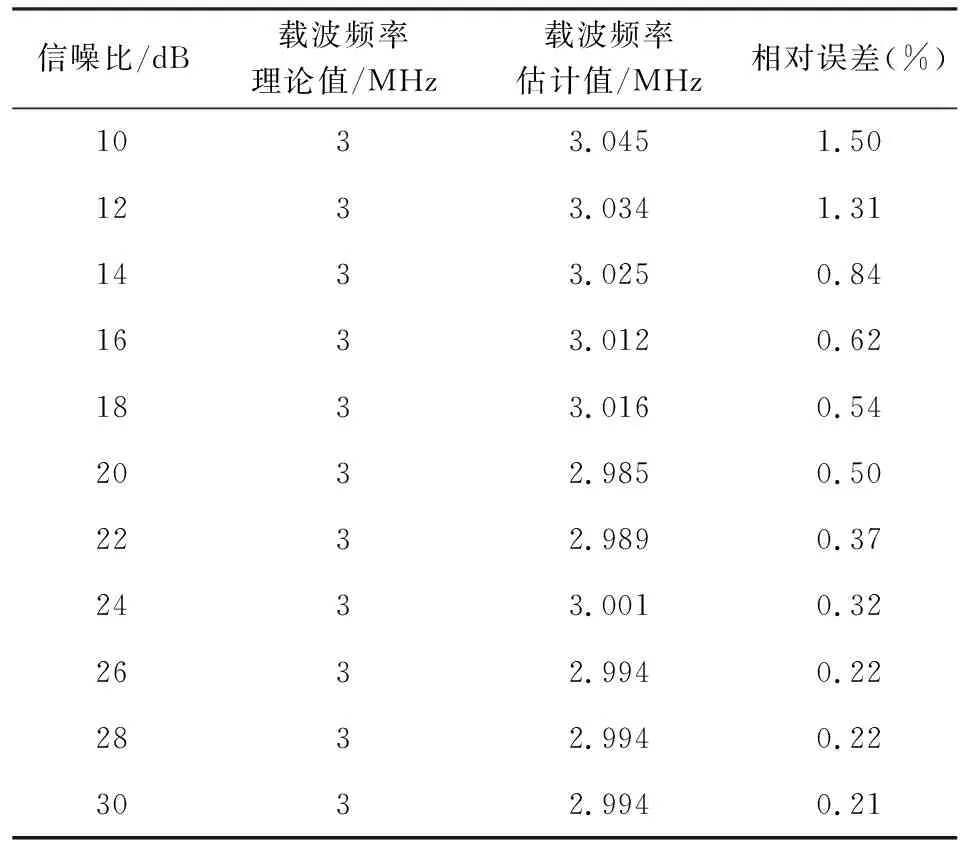
表2　不同信噪比下信号载波频率的相对误差

不同信噪比下信号载波频率的相对误差和信噪比的关系，如图10所示。

从表2可以看出，当信噪比为10 dB时，相对误差为1.50%，而当信噪比增大到30 dB时，相对误差减少到0.21%。并通过相对误差曲线图10表明，随着信噪比增大载波频率理论值与载波频率估计值之间的相对误差逐渐变小，而且愈来愈趋近一个稳定值，从而说明本文算法具有一定的稳定性。

4　结语

提出一种基于指数变换时频图像增强的FSK信号特征提取算法，该算法在时频图的基础上，先进行灰度转化和图像增强，然后对时频二维灰度图的灰度值矩阵进行特征参数ASM能量的提取，最后通过ASM能量曲线波峰区分出信号的载波频率。通过仿真实验，该算法能估算出信噪比在10 dB和30 dB下的ASM能量值、载波频率值和对应的谱线位置，从而区分出信号的载波频率，且根据性能实验表明，载波频率理论值和估计值的误差随着信噪比变大而愈来愈小，并趋近一稳定值，表明算法具有一定的可行性和稳定性。