移动GPU可重构背面剔除单元设计与实现

蒋　林, 郭佳乐, 邓军勇, 田汝佳, 张雪婷, 樊　萌

(西安邮电大学 电子工程学院， 陕西 西安 710121)

随着手机、PDA、掌上游戏机、便携式GPS等移动设备的普及[1]，移动图形处理器(graphic processing unit，GPU)得到了飞速发展[2]，但因受功耗和体积限制，其对能效和灵活性有着严格要求[3]。

无论图形处理器绘制管线是处在固定绘制管线、可编程绘制管线还是统一着色器绘制管线[4-6]，出于保证图形正确显示、增强图形真实感、减少GPU绘制过程中的处理量和提高执行效率的目的，对其都需要进行“背面剔除”[7-9]。通过剔除不可见的背面，可以降低GPU的计算量，并减少扫描转换和染色过程的处理复杂度，然而，背面剔除算法实现形式较多，需要针对不同计算形式设计不同专用硬件结构[10]，无法达到移动GPU对电路灵活性的要求。

本文将针对不同计算形式，给出一种可重构背面剔除单元的并行化实现方法。该方法采用兼顾通用处理器(general purpose processor，GPP)灵活性和专用集成电路(application specific integrated circuit，ASIC)高效性的可重构阵列处理器[11]，完成具有不同计算形式的背面剔除单元的并行化映射，并在FPGA开发板上完成原型验证。

1　可重构阵列结构

采用可重构阵列处理器[12]，通过轻核处理单元(processing element，PE)之间部分寄存器共享的方式，实现相邻PE间的数据交互。每4×4个PE组成一个阵列处理器簇(processing element group，PEG)，阵列处理器簇通过两级交换结构实现4×4个分布式随机存取存储器(random access memory，RAM)的共享访问，每个RAM的大小为512×32比特，用来满足图形处理算法所需要的数据带宽。采用一个全局指令存储器对不同算法进行存储，并通过全局控制器实现指令下发。

可重构阵列处理器的结构如图1所示，其中虚线部分为邻接互连通信，通过PE间共享寄存器进行数据交换；灰色部分为阵列处理器簇内两级交换结构，每个PE均可实现本地RAM的优先访问(PE编号与RAM编号相同则为本地RAM)以及4×4个分布式RAM的共享访问。

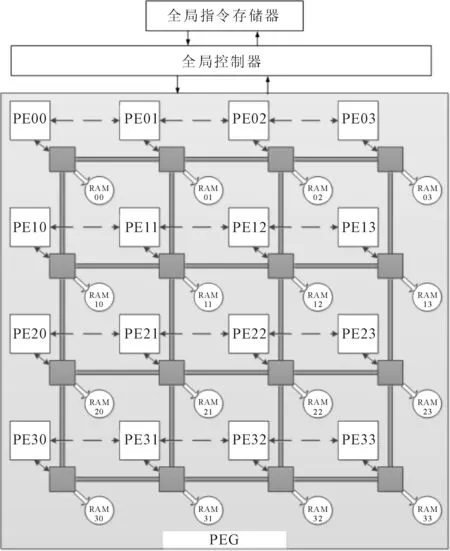
图1　可重构阵列处理器结构

2　可重构背面剔除单元的设计

2.1　OpenGL中的背面剔除

OpenGL(open graphics library)[13]可以通过glEnable()函数和glDisable()函数来开启和禁用剔除功能，通过glFrontFace()函数确定多边形的正面，以及通过glCullFace()函数剔除多边形的表面。其中，glFrontFace()函数有两种mode参数，分别为GL_CCW(顶点顺序为逆时针方向的表面为正面)和GL_CW(顶点顺序为顺时针方向的表面为正面)。glCullFace()函数有三种mode参数，分别为参数GL_FRONT(表示正面多边形)，参数GL_BACK(表示背面多边形)，参数GL_FRONT_AND_ BACK(表示所有多边形)[14]。

对于3个顶点分别为A(x1，y1，z1)，B(x2，y2，z2)，C(x3，y3，z3)的三角形，有

a=N·S=(x1y2-x2y1)+
(x2y3-x3y2)+(x3y1-x1y3)。

(1)

式(1)可化简为

a=b1+b2+b3，
b1=x1(y2-y3),
b2=x2(y3-y1),
b3=x3(y1-y2)。

(2)

通过式(1)或式(2)中a值的正负性与三角形顶点的方向，可判断正面或背面[14]，并通过glCullFace()函数中的参数进行是否剔除处理，其主要关系如表1所示。

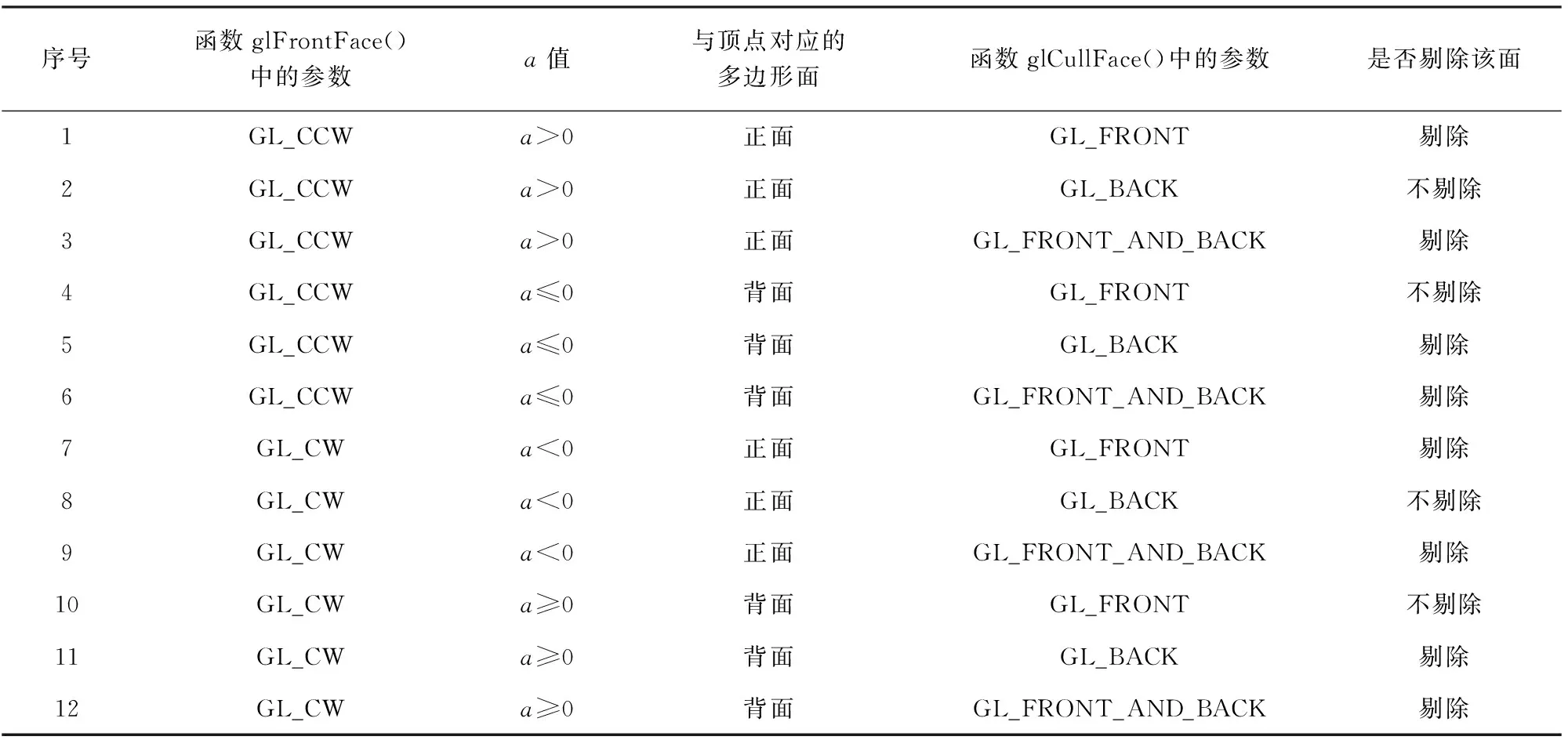
表1　函数glFrontFace()和glCullFace()及a值对应的多边形面剔除情况

2.2　背面剔除算法的并行化实现

将并行化实现过程分为5大部分，分别为乘法运算单元设计、数据拆分与准备、a值计算方式实现、最终计算结果的拼接输出以及不同a值计算方式的可重构切换等。其中对a值的计算分别采用式(1)和式(2)进行设计，实现两种不同形式的计算。

(1) 乘法运算单元设计

根据背面剔除算法，无论是式(1)还是式(2)，a值计算中最主要的为乘法运算，考虑到直接使用乘法器会增加电路复杂度，为简化电路，采用移位加的方式实现一个乘法运算。根据可重构阵列结构的特点，以A乘以B为例，其流程如图2所示。

(2) 数据的准备与拆分

通过PE10和PE01邻接互连的外围连线将数据x1、x2、x3和y1、y2、y3进行输入，将y1、y2、y3分别放入PE01的1、2、3号地址，将x1、x2、x3分别存储在PE10、PE11、PE12的4号地址中。由于可重构阵列处理器的数据位宽为32位，所要处理的顶点数据也均为32位，为了能够精确的表示a值，需要将最终的乘法运算结果采用64位进行表示。为了能够简化乘法运算，提高计算效率，根据阵列处理器的特点，对x1、x2、x3分别采用如图3所示的两种方式进行拆分，对y1、y2、y3采用如图3(b)所示的方式进行拆分。并将拆分后的数据进行y2-y3、y3-y1、y1-y2高20位和低12位的计算，用来实现公式(2)，通过阵列处理器簇内两级交换结构将所需要的数据分别放入对应PE的存储器中，以便于后续的数据读取。

图2　移位加实现乘法流程

图3　两种数据拆分方式

(3)a值两种计算方式的并行化实现

a值计算公式(1)的实现：以x1y2为例。记x1高10位为x1H10，x1中间10位为x1M10，x1低12位为x1L10，x1高20位为x1H20，x1低12位为x1L12，y2高20位为y2H20，y2低12位为y2L12。

经过数据拆分后，将该乘法分为了5部分:x1H10乘以y2H20,x1M10乘以y2H20,x1L10乘以y2H20,x1L12乘以y2L12,x1H20乘以y2L12。

为了简化乘法运算的复杂度，提高计算的并行程度，采用图2所描述的方式,将这5部分乘法使用5个PE进行计算，并最终通过15个PE完成a值计算公式(1)的映射。

如图4所示，将各部分乘法结果采用邻接互连的方式通过空心箭头的指向进行传输，在PE02、PE12、PE22、PE32、PE33中拆分过后的各部分数值求和，分别记为a1、a2、a3、a4、a5，通过阵列处理器两级交换结构将数据存储在PE33的100—104号地址中。其中，a1的表示方式为

a1=(x1H10y2H20-x2H10y1H20)+
(x2H10y3H20-x3H10y2H20)+
(x3H10y1H20-x1H10y3H20。

a2、a3、a4、a5依此类推。

图4　a值计算公式(1)映射结构

采用邻接互连的方式，通过黑色箭头的指向来传递各部分完成时的标志信号flag，在PE33的寄存器中放入整个公式计算完成的标志信号。

a值计算公式(2)的实现：以x1(y2-y3)为例。记x1高10位为x1H10，x1中间10位为x1M10，x1低12位为x1L10，x1高20位为x1H20，x1低12位为x1L12，y2-y3高20位为(y2-y3)H20，y2-y3低12位为(y2-y3)L12。经过数据拆分后，将乘法分为5部分，分别为x1H10(y2-y3)H20、x1M10(y2-y3)H20、x1L10(y2-y3)H20、x1L12(y2-y3)L12、x1H20(y2-y3)L12。映射过程如图5所示。

图5　a值计算公式(2)映射结构

在PE02、PE12、PE22、PE32、PE33中,拆分过后的各部分数值求和，分别记为a1、a2、a3、a4、a5，通过阵列处理器两级交换结构将数据存储在PE33的100—104号地址中。其中，a1的表示方式为

a1=x1H10(y2-y3)H20+
x2H10(y3-y1)H20+x3H10(y1-y2)H20。

a2、a3、a4、a5依此类推。采用与式(1)相同的方式实现整个公式完成标志。

(4) 最终计算结果的拼接输出

无论是采用公式(1)还是公式(2)实现a值的计算，均会通过阵列处理器两级交换结构将最终结果写入到PE33的100—104号地址中，为此只需使用PE33邻接互连的外围连线将所计算出的数据a1—a5进行连续输出，并通过左移的方式实现数据的拼接，输出最终的a值。其中a1左移34位，a2左移24位，a3左移12位，a4左移12位，a5保持，对其左移后的数据相加之后得到最终的得到最终的a值。

(5) 不同a值计算方式的可重构切换

为了调用不同的a值计算公式来实现背面剔除算法完成可重构的设计，提高电路的灵活性，将两种不同的实现方法分别存储在全局指令存储器中，在计算开始之前，全局控制器根据外部给出的算法使能信号flag_select选取a值计算方式，将所选取的算法指令依照H型网络，通过指令传输网络将指令依次下发到各个PE中，并在下发结束后启动PE阵列开始计算。全局控制器可根据算法使能信号flag_select实时动态的实现a值计算方式切换，实现多种图形渲染算法的指令下发传输，还可以控制PE的执行和结束，通过不同的配置信息来实现算法的动态重构。

3　结果与分析

3.1　原型实现

测试所给方法的正确性和可行性。将所给方法接入文献[15]所提的结构中，选用Xilinx的Virtex6系列FPGA对本文所实现的方法通过全局控制器以可重构的方式分别进行原型实现。测试采用线框模式来绘制一个金字塔，将glCullFace()参数分别设置为GL_FRONT、GL_BACK、GL_FRONT_AND_BACK；glFrontFace()参数分别设置为GL_CW和GL_CCW，绘制结果如图6所示，其工作频率为121.18 MHz。

图6　绘制结果

3.2　对比分析

在FPGA开发板上进行原型验证后，与文献[10]所给方法相比，结果如表2所示。所给可重构背面剔除单元设计方法可以实现同一种阵列结构两种不同形式的并行化映射，提高了电路的灵活性，为移动图形处理器的灵活性设计提供了新思路。

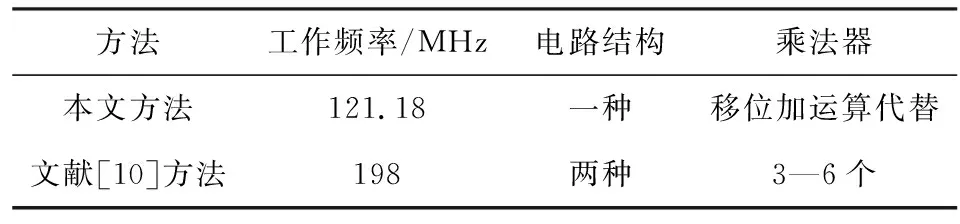
表2　性能对比

4　结语

为了适应移动图形处理器的高能效和图形渲染多样性的特点，根据可重构阵列结构，给出一种可重构背面剔除单元的设计方法，用可重构的方式灵活的实现两种不同形式的a值计算。在Xilinx的Virtex6系列FPGA开发板上分别进行原型实现，并对glCullFace()函数和glFrontFace()函数的不同参数情况进行测试。实验结果表明，所给可重构背面剔除单元并行化映射实现方法，能够正确计算两种不同实现形式的背面剔除算法，在不同参数情况进行正确剔除的同时，灵活性大大提高，且更加实用。