基于MATLAB编程Dijkstra算法的消防救援最佳路线研究
2018-07-12曾庆福王孟平
曾庆福,王孟平
(1.苏交科集团(江苏)安全科学研究院有限公司; 2.中国石化扬子石油化工有限公司,江苏 南京 211100)
0 引言
近年来城市火灾问题成为困扰社会公共安全的一大难题,特别是人员密集场所,如大型商场、游乐场等,做好公共安全风险管理[1],配备相应的消防设备、设施及专业安全人员,一旦发生火灾,争取在最短的时间内、使用最有效的措施和最小的能耗来扑救火灾,以减少人员伤亡和财产损失。经过对大量火灾案例的调查和研究,不难发现,火灾发生后,能否及时进行火灾扑救也是造成人员伤亡、财产损失和环境污染的重要原因,因此研究消防力量覆盖区域内的最佳救援路线,建立应急预案体系,使专业消防人员第一时间到达火灾现场就成了当务之急[2]。虽然前人已做了大量关于火灾和消防的研究,也取得很大成就,但针对火灾后专业消防队如何以最短时间抵达火灾现场,即消防站到火灾现场最佳路线问题研究较少。而最佳救援路线的选择又避免不了最短路径的计算,常用最短路径算法有:Dijkstra算法[3-4]、A*算法[5]、K-均值算法[6]等。本文运用Dijkstra算法,并综合考虑影响消防救援的各种不确定因素,结合GIS和Earth-map技术,实现消防救援最佳路线的选择。
1 经典Dijkstra算法的基本思想及数学模型
1.1基本思想
Dijkstra算法的基本思想是从某一点(vs)开始,依次向外探寻最短路径。此过程中,对于每一个点,都要记下一个相应的数(即该点的标号),若此数表示从起点vs到该点的最短路径的权值,则用P标号,反之表示从起点vs到该点的最短路径的权值上界,即用T标号,算法的每一步就是修改T标号的点为P标号的点,使赋权有向图D中的点全部转化为P标号的点,至多经过p-1步,方可求出从起点vs到终点的最短路径。
1.2数学模型
Dijkstra算法的数学模型为:给定赋权有向图D=(V,A)。令Si表示P标号节点集合;P(vs)表示到节点vs的最短路径;λ(vs)表示到节点vs的最短路径上前一个点。初始化:i=0,S0={vs};P(vs)=0;λ(vs)=0;T(v)=+∝,v∉Si。
①若Si=V,即v∈Si,v∈V,则算法终止;否则转入②。
②对于Akj=(vk,vj)∈A,vj∈Si;若T(vj)>P(vk)+tkj,则令T(vj)=P(vk)+tkj;否则转入③。
③P(vji)=T(vji)=min{T(vj)},Si+1=Si∪{vji}。
④若V=S,表明vk到所有节点最短路径已确定,则算法结束;否则转入②继续确定其他节点最短路径。
2 影响消防覆盖区域内最佳路线选择的因素
2.1外部因素
关于消防力量覆盖区域内,影响消防救援最佳路线选择的外部因素分析,主要是考虑影响消防车辆由消防站到火灾现场过程中,存在的各种不确定因素,诸如天气、路质、路况等。而这些外部因素的不确定性,又进一步加剧消防车辆的行驶难度。一般情况下,道路周边环境不同,车流、人流量也不同,如居民小区、学校区域及城市主干道的车流、人流量就比较大,车速缓慢;而早晚班点、上下学时段,车流、人流量大,道路拥堵,影响车速;特别是雾霾天气和雨雪天气,路面湿滑,摩擦性小,能见度低,易发生事故,车辆行驶速度慢,所以严重影响消防车辆行驶,延长行驶时间。文中用m,b和a来表示外部因素天气、路质和路况[7],其取值范围如表1和表2所示[6]。
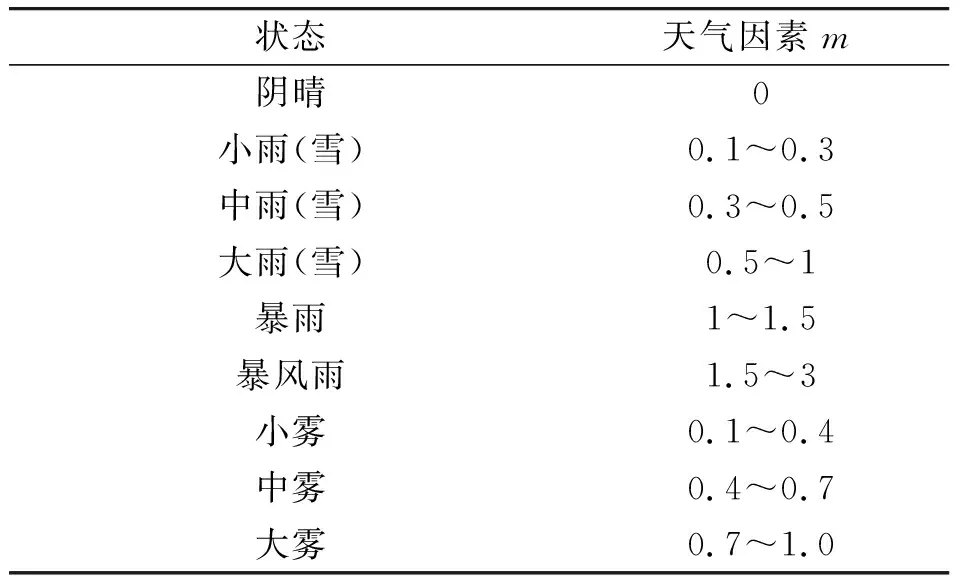
表1 天气因素m的取值范围
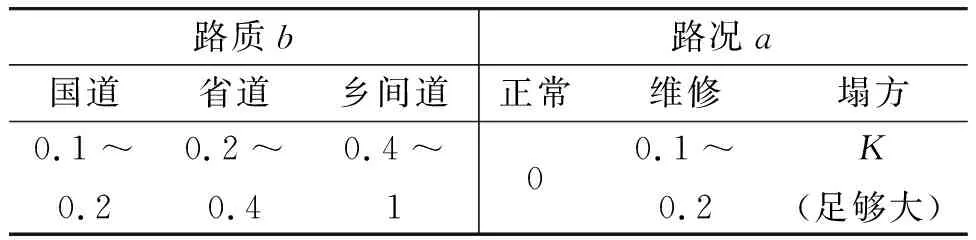
表2 路质因素b和路况因素a的取值范围
2.2内部因素
影响消防救援最佳路线选择的内部因素,主要考虑消防人员和消防车辆两个方面。而把消防人员作为分析对象,主要考虑到消防人员对火灾现场具体地理位置的熟悉程度,能否迅速、准确地到达火灾现场。再者消防站接到消防力量调度中心的火警通知,出警的迅速度以及消防车辆驾驶员的驾驶特性和道路熟悉度等都影响消防车辆驾驶人员选择最佳路线通往火灾现场。另外消防车辆上的设备安装,特别是导航设备和通信设备是否安装且保持良好,都会影响消防救援最佳路线的选择和消防车辆行驶时间的控制。
3 消防力量覆盖区域内最佳救援路线选择
3.1绘制公路网络拓扑结构
为了研究消防力量覆盖区域内的最佳救援路线,以阜新市海州区消防力量覆盖区域内局部交通网络图为研究对象,利用GIS和Earth-map技术实现该区道路交通网络的可视化和地理位置信息获取[8-10],并绘制出由点和边组成的公路网络静态拓扑结构[11],如图1所示。图中节点v1为消防站所在地,设定节点v24为火灾事故现场。
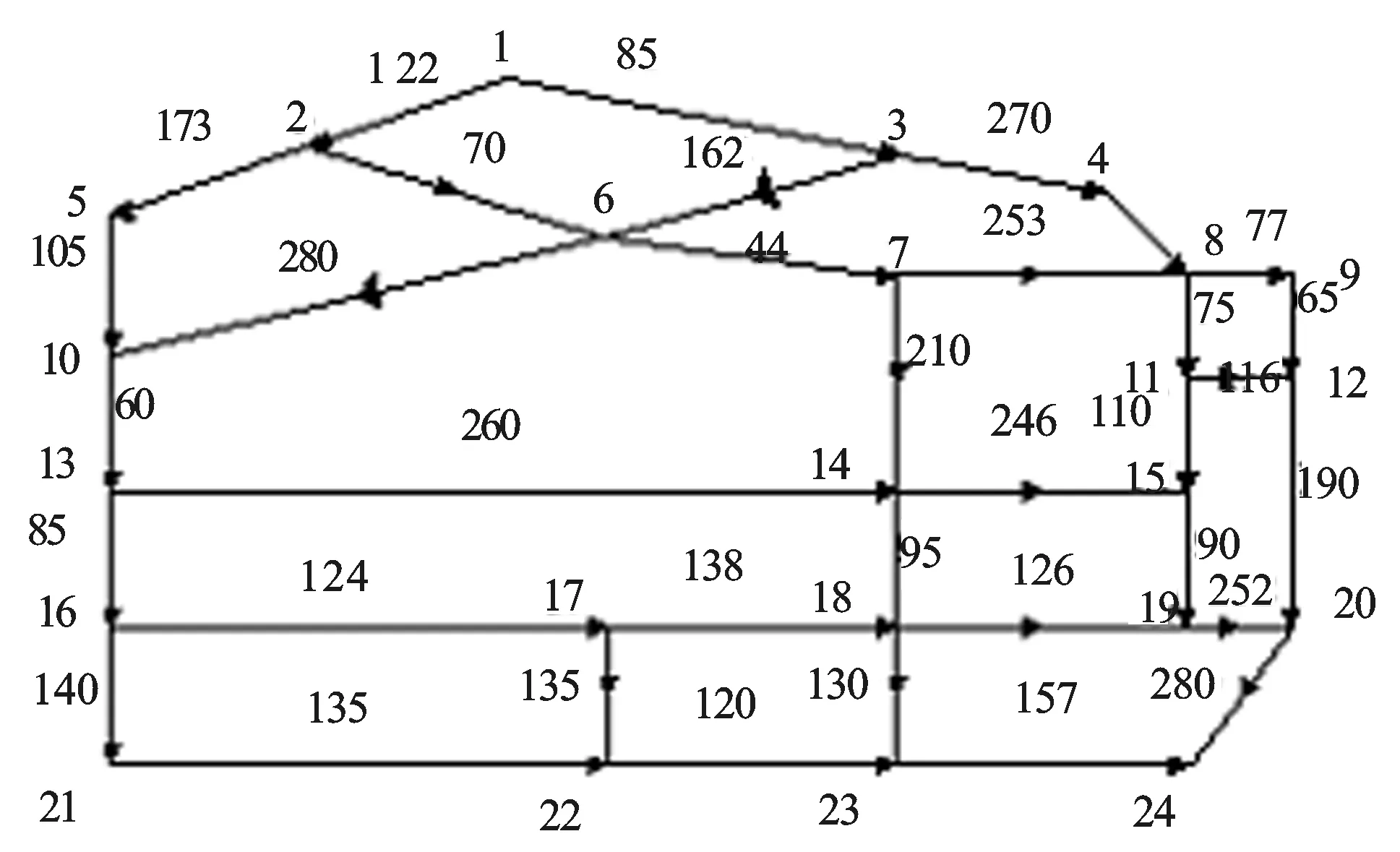
图1 网络拓扑结构
3.2Dijkstra算法的MATLAB实现
根据上文绘制的公路网络静态拓扑结构关系以及图中所标的道路实际长度,运用MATLAB编程软件来实现Dijkstra最短路径算法。由软件可求得,消防站到消防力量覆盖区域内各节点的最短距离及路径,如表3所示。表3中虽未逐一列出消防站到任意一点的最短距离和路径,但表中所列举的最短路径中已包含网络拓扑关系中的所有节点,故消防站到其余节点的最短路径无需再一一列举。

表3 消防站到消防力量覆盖区域内任意一点的最短距离及路径
3.3最佳救援路线选择
3.3.1时间修正系数
时间修正系数是指在考虑影响消防车辆行驶的各种不确定因素情况下,消防车辆行驶时间与消防车辆在理想情况下行驶时间的比值,用K值表示。
前文已分析消防力量覆盖区域内影响消防车辆行驶的各种不确定因素,而在这些因素的影响下,消防车辆的行驶速度随时间不断变化,因此不能仅仅取道路交通网络中,任意相邻两节点间实际道路长度与速度的比值来确定消防车辆行驶时间,而是考虑各种影响因素将道路实际长度转化为道路计算长度,利用平均速度进行行驶时间计算[12],其道路计算长度表达式为:
L=l*[1+b(1+m)+a](1)
消防车辆行驶的平均速度表达式为:
(2)
故消防车辆行驶时间为:
=Kl/v0
(3)
K=[1+b(1+m)+a]a1a2a3
(4)
式中,v0表示消防车辆在城镇道路上行驶的最大速度,一般取50 km·h-1;a1为道路坡度影响系数,当道路坡度J>0时a1>1,当J=0时a1=1,当J<0时0
3.3.2消防车辆到达消防力量覆盖区域内各点的行驶时间
根据《城镇消防站布局与技术装备配备标准》和《城市消防站建设标准》规定,消防车辆的平均行驶速度取30~36 km·h-1;而市内道路无明显坡路,故坡度影响系数a1=1;且路面多为沥青路面或水泥路面,多数情况路面平整,故路面影响系数a3=1;由于阜新市是小型城市,人口密集且街道狭窄,道路曲折(曲度系数一般为1.3~1.5),故车辆行驶速度慢,曲度系数可取最大值a2=1.5;上述计算在天气晴朗、能见度良好、路况正常的城市道路上进行,即m=a=0和b=0.2,则其消防车辆行驶时间、道路计算长度和时间修正系数如表4所示。
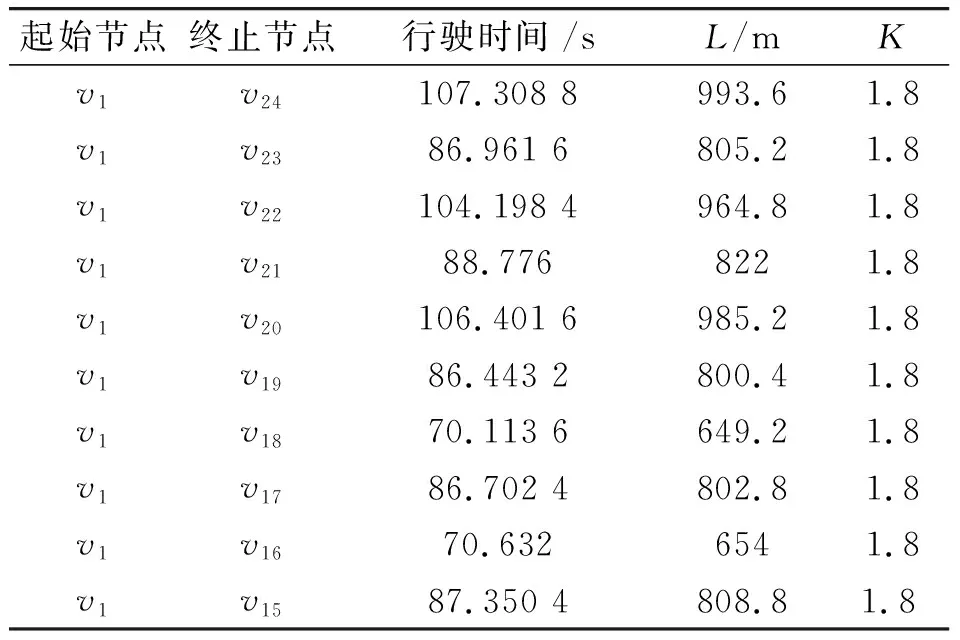
表4 消防车辆行驶时间、道路计算长度和时间修正系数
由表4可知,在天气晴朗、能见度良好和路况正常的城市道路条件下,消防站到火灾现场的最佳救援路线选择,可以用消防车辆的行驶时间来表示,即消防车辆在消防力量覆盖区域内各点到消防站的最短路径上行驶,所需用的时间来表示。而消防救援讲究把握有利战机,需要严格控制消防车辆行驶时间,因此消防车辆行驶时间最短的路线,即为消防救援最佳路线。故消防站(v1)到火灾现场(v24)的最短距离为828 m,消防车辆行驶时间为107.308 8 s,最佳救援路线为v1,v2,v6,v7,v14,v18,v23,v24,具体如图2所示。
下文将在上述基础上讨论几种恶劣气候条件,如大雾、中雾和大雨雪、中雨雪等对道路交通的影响,分析比较节点v1到节点v24间最佳救援路线上消防车辆行驶时间。其中两节点间的道路实际长度一致(l=828 m),但考虑外部因素及其取值不同,故得到的时间修正系数K值也不同,并且不同的外部因素影响下消防车辆的行驶速度不尽相同,从而使得道路计算长度和消防车辆行驶时间发生变化,而《道路交通安全法实施条例》规定驾驶机动车辆遇到雾、雨、沙尘、冰雹等天气,能见度在50 m以内时,最高行驶速度不得超过30 km·h-1,具体计算结果见表5所示。
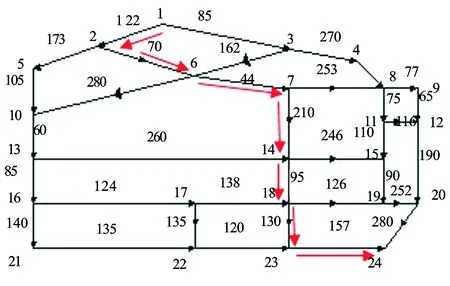
图2 最佳救援路线
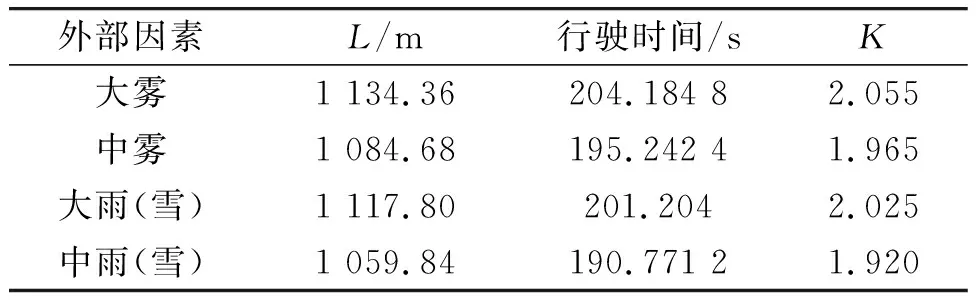
表5 几种特殊的外部因素对消防车辆行驶的影响
由表5可知,在上述严峻的外部因素影响下,同样由消防站到火灾现场这段距离,消防车辆的行驶时间明显增加。
为了清楚反映消防车辆的行驶时间与外界环境间的密切关系,使用origin绘图软件,绘制行驶时间和时间修正系数K值的关系,如图3所示。图3中反映了时间修正系数随着外界环境条件的不同而改变,并且行驶时间随着时间修正系数的增大而不断延长,不利于消防人员第一时间到达火灾现场实施火灾扑救。
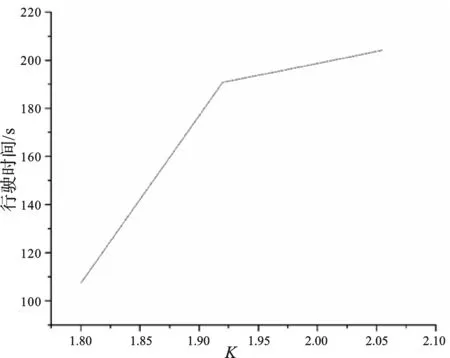
图3 行驶时间与时间修正系数
4 结论
4.1采用经典的Dijkstra算法,运用MATLAB编程软件实现消防力量覆盖区域内消防站到火灾现场间的最短路径。综合分析各种影响因素将实际道路长度转化为道路计算长度,使用平均速度,引进时间修正系数(K),使消防车辆行驶时间的求解精确度提高,而行车时间最短的路径为最佳路径,更有利于消防人员到达火灾现场扑救火灾。
4.2结合阜新市海州区局部消防力量覆盖区域内某点火灾时的消防车辆行驶路线为例进行分析,可知无论外部环境条件良好还是恶劣,上述算法实现的消防力量覆盖区域内最佳路径上消防车辆行驶时间,皆符合我国《城镇消防站布局技术装备配备标准》规定的行车到场4 min的要求,能够及时进行火灾扑救。但是恶劣环境条件下同样的行程所需行车时间较长,因此消防力量覆盖区域内最佳路径的研究对消防救援工作意义重大。
